Цифровой фильтр

Эквалайзер

Часто при обработке звука мы хотим изменить его характер/окраску/тембр. Сделать звук более басовым, убрать верхние частоты, или наоборот, сделать звук «прозрачным», оставив лишь середину и верха. Уверен, многие люди, не работавшие с обработкой звука, знают что такое эквалайзер — они есть акустических колонках, музыкальных центрах, магнитофонах, плеерах, и т.д. Эквалайзер — это набор фильтров, каждый из которых изменяет амплитуду сигнала в его выбранной полосе частот. На бытовых колонках это, обычно, 2-3 крутилки — низкие частоты, средние и верха, с фиксированными полосами частот.

В Winamp’овском эквалайзере уже есть 10 заранее определенных полос.

Скриншот эквалайзера в плеере Winamp

В мире обработки звука существует множество плагинов-эквалайзеров, на любой вкус и цвет. Плагин Fab Filter Pro Q (скриншот в начале статьи) — это графический эквалайзер, позволяющий создавать большое число полос и редактировать их параметры.

Каждая полоса в эквалайзере — это, по сути, фильтр частот. Фильтры частот изменяют тембральные/частотные характеристики сигнала. В электронике существуют много типов и классификаций фильтров, с соответствующими характеристиками и параметрами — смотрим википедию.
Мы рассмотрим и запрограммируем самые простые фильтры: НЧ, ВЧ и полосовой фильтры.

«Глупые» часы на FPGA

Tutorial

Привет всем!
Решил написать очередную статью, которая была бы полезна начинающим разработчикам в области ПЛИСоводства. Очень долго откладывал момент публикации, сам материал подготовил еще несколько месяцев назад, а вот сесть и написать всё это в целую статью как-то не доходили руки. Но вот наконец-то появилось свободное время, поэтому всех заинтересовавшихся приглашаю к прочтению.
Проект называется «глупые часы», поскольку он ничего не умеет, кроме как считать время и дату и выводить их на дисплей. В первую очередь проект рассчитан на студентов старших курсов и новичков. В нём нет никаких необычных блоков, не используются вендорные IP-ядра, и уж тем более нет сложных интерфейсов обмена (типа PCIe, Ethernet, USB и т.д.).
В этот раз проект на программируемых логических интегральных схемах (ПЛИС) будет примитивен и предельно прост, а я постараюсь рассказать обо всех трудностях, с которыми пришлось столкнуться при выполнении поставленной задачи.

Программирование фильтра Баттервота по полученным формулам

Фильтр будет иметь 2 параметра: тип фильтра (НЧ, ВЧ, полосовой) и частота среза w. Для полосового фильтра будем рассматривать частоту среза как частоту посередине полосы пропускания. Полосу пропускания же определим как отрезок частот [w — w/4, w + w/4] (можно придумать здесь более сложный и логичный здесь логарифмический закон, на ваше усмотрение).

Пусть мы определили коэффициенты b0, b1, b2, a1 и a2 (a0 по условию равен 1) по рассчитанным формулам. Алгоритм работы фильтра сводится к свертке, которая делается последовательно для каждого семпла:

y(n) — это новое значение семпла, которое нужно рассчитать. x(n) — текущее значение семпла, соответственно y(n-1) и y(n-2) — предыдущие 2 рассчитанных семпла, а x(n-1) и x(n-2) — предыдущие входные значения семплов.

Нужно организовать запоминание предыдущих семплом. Не будем мудрить с циклическими буферами, сделаем просто и понятно: два массива из трех элементов. Каждый раз будем «проталкивать» новые значения в этот массив, последовательно копируя более старые значения семплов.

Получаем простой класс:

Напишем каркасный класс для фильтра (смотри архитектуру синтезатора в первой статье). Класс BiquadConvolutionTable работает с одним сигналом, т.е. с одним каналом — моно. Поэтому нам нужны две BiquadConvolutionTable — для левого и правого каналов.

Чтобы корректно применить фильтр, нужно последовательно, для всех семплов входящей последовательности применить функцию BiquadConvolutionTable.Process и заполнить результирующий массив семплов.

Рассчетом коэффициентов для BiquadConvolutionTable будет заниматься функция CalculateCoefficients.

Функция CalculateCoefficients вызывается каждый раз в цикле — зачем? В следующей статье я расскажу про модуляцию (изменение во времени) параметров, и поэтому, частота среза может меняться, а значит, нужно перерассчитывать коэффициенты. Конечно, по-трушному, нужно подписаться на изменение частоты среза и уже в обработчике рассчитывать коэффициенты. Но в этих статьях я оптимизами заниматься не буду, цель — закодить фильтр.

Осталось закодить функцию CalculateCoefficients по рассчитаным формулам для коэффициентов.
Вспомним, что нужно использовать денормированные частоты, т.е. произвести замену:

Списываем все формулы для коэффициентов b0, b1, b2, a0, a1, a2. После рассчетов нужно поделить все коэффициенты на a0, чтобы a0 стало равно 1.

Разница между аналоговыми и цифровыми фильтрами

Тип обработанного сигнала

Аналоговые фильтры может обрабатывать аналоговые фильтры напрямую.

Цифровые фильтрынеобходимо сначала преобразовать аналоговые сигналы в цифровые, перед обработкой. После обработки сигнал необходимо снова преобразовать из цифрового в аналоговый.

Изменение функциональности

Чтобы изменить функционированиеаналоговые фильтрысами компоненты должны быть переконфигурированы.

Цифровые фильтры обычно регулируются алгоритмами, и функциональность может быть легко изменена путем изменения этих алгоритмов.

Скорость обработки

Аналоговые фильтры отфильтровывать нежелательные частоты непрерывно.

Скорость, с которой цифровые фильтры может работать в зависимости от частоты их выборки.

Изображение предоставлено

«Принципиальная схема примера полосового фильтра в топологии Кауэра Т-образного сечения…» по Inductiveload (собственная работа) , через

Квадратные фильтры (и системы фильтров)

А что насчет тех квадратных кусочков стекла, которыми пользуются некоторые пейзажные фотографы? Это тоже фильтры, обычно – ND или GND, но существуют и квадратные поляризаторы (это звучит странно, ведь, с технической точки зрения, они называются квадратными циркулярными поляризаторами). Зачастую фотографы устанавливают стандартный поляризационный фильтр на одной из сторон квадратного держателя, чтобы иметь для него возможность независимого регулирования.

Квадратные держатели фильтров прикрепляются к объективу при помощи специальных адаптеров, подходящих под размер резьбы.

Преимущество такой системы в том, что не нужно прикручивать и откручивать фильтры. Вы просто вставляете квадратный кусочек стекла и вынимаете его, когда нужно. Либо, в случае с большинством моделей, просто откидываете держатель, компонуете кадр и фокусируетесь, а затем закидываете его обратно. Это может сохранить огромное количество времени при работе с плотными ND-фильтрами, ведь с ними почти невозможно увидеть что-либо сквозь видоискатель.

Я в основном использую именно этот тип и очень его люблю, хотя во многом всё зависит от личных предпочтений. Многие потрясающие фотографы отдают предпочтение исключительно круглым фильтрам, поэтому вам нужно самостоятельно определиться с видом, который лучше подходит. Есть множество хороших держателей для квадратных фильтров от компаний Lee Filters, Cokin, Breakthrough Photography, а также недорогая версия от The Filter Dude.

Тестер микросхем

Опубликовано вт, 09/05/2017 — 15:45 пользователем trol

Устройство предназначено для тестирования логических микросхем, операционных усилителей, оптопар, и некоторых других элементов.
Из логических микросхем поддерживаются отечественные (серии 155, 555, 1531, 1533, 176, 561, 1561, 1564, 580, 589 и др.) и импортные
(74ххх, 40ххx, 45xxx) ИМС ТТЛ и КМОП. Меню и результаты проверки отображаются на цветном дисплее 128х128.
Так же тестер умеет проверять микросхемы DRAM, SRAM, считывать EPROM и показывать, есть ли в них записанные данные.
Кроме того, прибор можно использовать при отладке различных цифровых устройств как интерфейс с 40 каналами ввода-вывода управляемыми по USB.

Тестер питается через miniUSB-порт, также через этот порт его можно подключить к компьютеру. Программное обеспечение позволяет разрабатывать,
запускать и пошагово отлаживать тесты, считывать содержимое ПЗУ и обновлять прошивку устройства.

Программное обеспечение написано на Java и является кроссплатформенным (Windows, Linux, MacOS X).

Реализация БИХ фильтра

Если рассматривается передаточная функция вида:

H(z)=Y(z)X(z)=∑k=Mbkz−k1+∑k=1Nakz−k=B(z)A(z),{\displaystyle H(z)={\frac {Y(z)}{X(z)}}={\frac {\sum _{k=0}^{M}b_{k}z^{-k}}{1+\sum _{k=1}^{N}a_{k}z^{-k}}}={\frac {B(z)}{A(z)}},}

то соотношение между входом и выходом такой системы должно удовлетворять разностному уравнению:

y(n)=−∑k=1Na(k)y(n−k)+∑k=Mb(k)x(n−k){\displaystyle y(n)=-\sum _{k=1}^{N}a(k)y(n-k)+\sum _{k=0}^{M}b(k)x(n-k)}

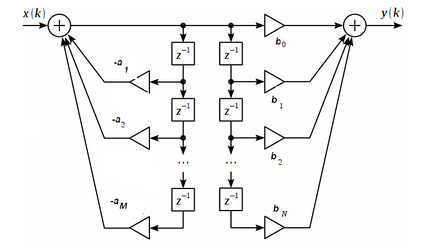
Это уравнение может быть записано непосредственно из выражения для передаточной функции, таким образом форму построения цепи, соответствующей этому уравнению, называют прямой формой 1.

Прямая реализация типа 1 БИХ фильтра

При построении БИХ фильтра для простоты можно принять, что M=N. БИХ фильтры могут быть реализованы с использованием трех элементов или основных операций: умножитель, сумматор и блок задержки. Этих элементов достаточно для всех возможных цифровых фильтров. Вариант, показанный на рисунке есть прямая реализация БИХ-фильтров типа 1.

Поскольку совокупности коэффициентов b(k) и a(k) соответствуют полиномам числителя B(z) и знаменателя A(z) передаточной функции Н(z), то прямую форму БИХ-фильтра, показанную на рисунке, можно трактовать как каскадное соединение двух цепей. Первая из них реализует нули и имеет передаточную функцию B(z), а вторая — полюсы, и имеет передаточную функцию 1/A(z). Обозначив выходной сигнал первой
системы w(n), разностное уравнение можно заменить системой уравнений:

y(n)=−∑k=1Na(k)y(n−k)+w(n),{\displaystyle y(n)=-\sum _{k=1}^{N}a(k)y(n-k)+w(n),}

w(n)=∑k=Mb(k)x(n−k){\displaystyle w(n)=\sum _{k=0}^{M}b(k)x(n-k)}

которая и реализована структурой, показанной на рисунке.

В дискретных системах с постоянными параметрами соотношение между входом и выходом не зависит от порядка каскадного соединения
блоков. Из этого свойства вытекает вторая прямая форма построения БИХ-фильтра. Если сначала реализовать полюсы H(z) соответствующие правой части структурной схемы верхнего рисунка, которая имеет передаточную функцию 1/A(z), а после — нули передаточной функцией B(z), то получим структуру, показанную на рисунке 2, которая соответствует системе уравнений:

w(n)=−∑k=1Na(k)w(n−k)+x(n),{\displaystyle w(n)=-\sum _{k=1}^{N}a(k)w(n-k)+x(n),}

y(n)=∑k=Mb(k)w(n−k).{\displaystyle y(n)=\sum _{k=0}^{M}b(k)w(n-k).}

Прямая реализация типа 2 БИХ фильтра (неканоническая)

Объединив линии задержки в структуре, показанной на верхнем рисунке, получим прямую каноническую форму БИХ-фильтра:

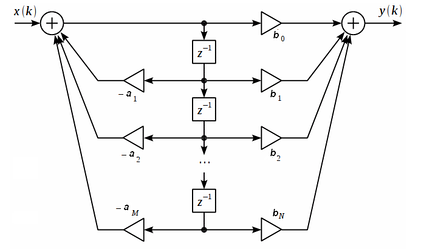
Прямая реализация типа 2 БИХ фильтра (каноническая)

В некоторых случаях, с точки зрения шумовых характеристик, фильтр, реализованный в прямой форме, лучше, чем в канонической.

Подключение АЦП к ПЛИС. Особенности, сложности, реализация

Всем привет! В данной статье речь пойдет о подключении микросхем АЦП к кристаллам ПЛИС. Будут рассмотрены основные особенности соединения узлов схем, представлены современные АЦП и их характеристики. В статье будут даны практические советы по быстрому и правильному подключению АЦП к ПЛИС с минимальными временными затратами. Кроме того, речь пойдет о принципах подключения тех или иных АЦП, будет рассмотрен входной буфер ПЛИС и его базовые компоненты – триггеры, узлы задержки IODELAY, сериализаторы ISERDES и т.д. Более детально с примерами программного кода на языке VHDL будет проведен обзор основных элементов, требуемых для качественного приёма данных от АЦП. Это входной буфер, узел упаковки данных для одноканальных и многоканальных систем, модуль синхронизации и передачи данных на базе FIFO, узел программирования АЦП по интерфейсу SPI, узел синтеза частоты данных – MMCM/PLL. Также в статье будет представлен обзор законченных устройств (в стандарте FMC) от ведущих зарубежных и отечественных производителей аналоговых и цифровых схем. В конце статьи вы найдете ссылку на исходные коды универсального узла приёмника данных от многоканальных схем АЦП. Код простой и гибкий в конфигурировании, он представлен на языке VHDL и заточен на микросхемы ПЛИС Xilinx 7 серии и выше, но может быть применен и в других кристаллах ПЛИС.

Круглый (циркулярный) поляризационный фильтр

Если вы когда-либо носили поляризующие очки, то испытали на себе эффект циркулярного поляризационного фильтра. Этот вид состоит из двух соединенных стекол, которые можно независимо поворачивать для регулировки силы поляризации. На практике вы видите результат на экране или смотрите сквозь видоискатель и поворачиваете поляризатор пока не получите желаемый результат.

Это обязательный аксессуар для любого фотографа.

Круглому поляризатору можно найти множество применений. Главное – эффекты, создаваемые с его помощью очень сложно или нереально воссоздать при помощи программной обработки. Как ни странно, свое название фильтр получил не из-за круглой формы. Оно относится к методу поляризации. Старые пленочные камеры использовали «линейные» фильтры. Они не позволяют замерять свет и работать с некоторыми видами автофокуса. Поэтому сейчас они устарели и почти не продаются

Обращайте внимание при покупке – вам нужен именно циркулярный поляризационный фильтр, хотя вряд ли сейчас можно встретить линейный тип

Поляризационный фильтр сокращает блики от сияющих предметов, например, воды или листьев. Когда вы впервые поработаете с поляризатором, вы будете удивлены, насколько много бликов есть на повседневных предметах. Особенно сильно без поляризатора блестит растительность. Правильное использование такого фильтра обеспечивает более богатые, глубокие и реалистичные цвета при съемке объектов, которые обычно отбрасывают блики.

А также такой фильтр может смягчить или убрать отражения на поверхности воды. Хоть иногда отражения и нужны, бывают ситуации, когда без них получается более интересное фото. Один из примеров – мелкое прибережье с интересными камнями под водой. Если небо отражается в воде, довольно трудно запечатлеть, что происходит под ее поверхностью. Однако, используя поляризатор, можно сделать воду кристально чистой и фотографировать происходящее на дне.

Поляризационные фильтры также делают синее небо более темным и глубоким

Хотя тут важно не перестараться, иначе получится нереалистичный вид. Но также, если снимать небо с очень широким углом и поляризационным фильтром, цвет в разных участках может отличаться

Это происходит из-за того, что эффект поляризатора варьируется в зависимости от угла падения солнечных лучей и при съемке с широкоугольником вы одновременно захватываете участки неба с разными углами. В таком случае лучше просто снять фильтр.

Частотомер-тестер кварцев на atmega8

Опубликовано чт, 01/18/2018 — 19:49 пользователем trol

Частотомер — полезный прибор в лаборатории радиолюбителя (особенно, при отсутствии осциллографа).
Кроме частотомера лично мне часто недоставало тестера кварцевых резонаторов — слишком много стало приходить брака из Китая. Не раз случалось такое,
что собираешь устройство, программируешь микроконтроллер, записываешь фьюзы, чтобы он тактировался от внешнего кварца и всё — после записи фьюзов
программатор перестаёт видеть МК. Причина — «битый» кварц, реже — «глючный» микроконтроллер (или заботливо перемаркированый китайцами с добавлением,
например, буквы “А» на конце). И таких неисправных кварцев мне попадалось до 5% из партии.
Кстати, достаточно известный китайский набор частотомера с тестером кварцев на PIC-микроконтроллере и светодиодном дисплее с Алиэкспресса мне
категорически не понравился, т.к. часто вместо частоты показывал то ли погоду в Зимбабве, то ли частоты «неинтересных» гармоник
(ну или это мне не повезло).