Цифровые функциональные узлы последовательного типа
Содержание:
- Двоичные асинхронные счётчики
- Счетчики с параллельным переносом
- 3.2 Тактируемые триггеры
- Реверсивный счетчик
- Счетчики с произвольным порядком пересчета
- 3 Задание к работе
- 5.3 Топологическое проектирование
- 6. TV-триггер
- Вычитающий счетчик
- Двоичные асинхронные счётчики
- 4.1 Моделирование TV-триггера
- 3.5 Счетчики с последовательным переносом
- Принцип работы операционного усилителя
Двоичные асинхронные счётчики
Простейший вид счётчика — двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера воспользуемся универсальным D-триггером с обратной связью, как это показано на рисунке 1.
Так как схема T-триггера при поступлении на вход импульсов меняет свое состояние на противоположное, то её можно рассматривать как счётчик, считающий до двух. Временные диаграммы сигналов на входе и выходах T-триггера приведены на рисунке 2.
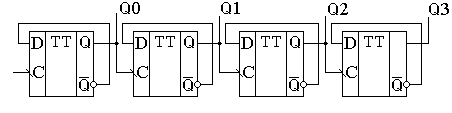
Обычно требуется посчитать большее количество импульсов. В этом случае можно использовать выходной сигнал первого счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два. Такой счетчик называется двоичным счетчиком, а тот факт, что состояние триггеров меняется на противоположное в различные моменты времени по мере распространения цифрового сигнала, отображается термином: асинхронный двоичный счетчик.
Схема счётчика, позволяющего посчитать любое количество импульсов, меньшее шестнадцати, приведена на рисунке 3. Количество поступивших на вход импульсов можно узнать, подключившись к выходам счётчика . Это число будет представлено в двоичном коде.
Для того чтобы разобраться, как работает схема двоичного счётчика, воспользуемся временными диаграммами сигналов на входе и выходах этой схемы, приведёнными на рисунке 4.
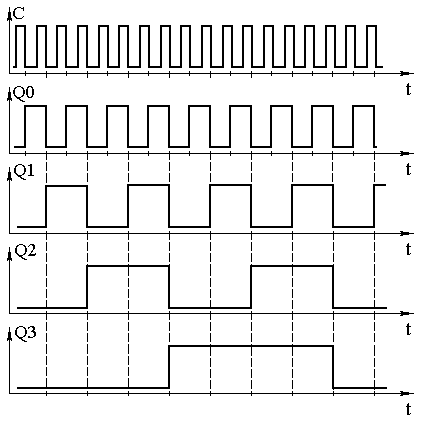
Пусть первоначальное состояние всех триггеров счётчика будет нулевым. Это состояние мы видим на временных диаграммах. Запишем его в таблицу 1. После поступления на вход счётчика тактового импульса (который воспринимается по заднему фронту) первый триггер изменяет своё состояние на противоположное, то есть единицу.
Запишем новое состояние выходов счётчика в ту же самую таблицу. Так как по приходу первого импульса изменилось состояние первого триггера, то этот триггер содержит младший разряд двоичного числа (единицы). В таблице поместим его значение на самом правом месте, как это принято при записи любых многоразрядных чисел. Здесь мы впервые сталкиваемся с противоречием правил записи чисел и правил распространения сигналов на принципиальных схемах.
Подадим на вход счётчика ещё один тактовый импульс. Значение первого триггера снова изменится на прямо противоположное. На этот раз на выходе первого триггера, а значит и на входе второго триггера сформируется задний фронт. Это означает, что второй триггер тоже изменит своё состояние на противоположное. Это отчётливо видно на временных диаграммах, приведённых на рисунке 4. Запишем новое состояние выходов счётчика в таблицу 1. В этой строке таблицы образовалось двоичное число 2. Оно совпадает с номером входного импульса.
Продолжая анализировать временную диаграмму, можно определить, что на выходах приведённой схемы счётчика последовательно появляются цифры от 0 до 15. Эти цифры записаны в двоичном виде. При поступлении на счётный вход счётчика очередного импульса, содержимое его триггеров увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков.
Таблица 1. Изменение уровней на выходе суммирующего счётчика при поступлении на его вход импульсов.
| номер входного импульса | Q3 | Q2 | Q1 | Q0 |
| 1 | 1 | |||
| 2 | 1 | |||
| 3 | 1 | 1 | ||
| 4 | 1 | |||
| 5 | 1 | 1 | ||
| 6 | 1 | 1 | ||
| 7 | 1 | 1 | 1 | |
| 8 | 1 | |||
| 9 | 1 | 1 | ||
| 10 | 1 | 1 | ||
| 11 | 1 | 1 | 1 | |
| 12 | 1 | 1 | ||
| 13 | 1 | 1 | 1 | |
| 14 | 1 | 1 | 1 | |
| 15 | 1 | 1 | 1 | 1 |
Условно-графическое обозначение суммирующего двоичного счетчика на принципиальных схемах приведено на рисунке 5. В двоичных счётчиках обычно предусматривают вход обнуления микросхемы R, который позволяет записать во все триггеры счётчика нулевое значение. Это состояние иногда называют исходным состоянием счётчика.
Существуют готовые микросхемы асинхронных двоичных счётчиков. Классическим примером такого счётчика является микросхема 555ИЕ5. Подобные схемы существуют и внутри САПР программируемых логических интегральных схем.
Счетчики с параллельным переносом
Для повышения
быстродействия применяют способ одновременного формирования сигнала переноса
для всех разрядов. Достигается это введением элементов И,
через которые тактовые импульсы поступают сразу на входы всех разрядов
счетчика. Посмотрим на схему:
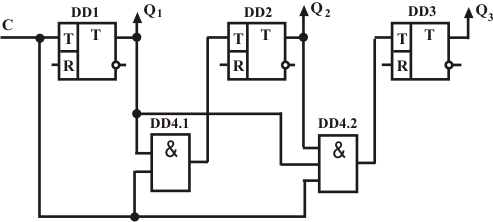
Рис. 2 Счетчик с параллельным переносом и графики, поясняющие его работу
С первым триггером все
понятно. На вход второго триггера тактовый импульс пройдет только тогда, когда
на выходе первого триггера будет лог. 1 (особенность схемы И), а на вход третьего — когда на выходах первых двух будет
лог. 1 и т. д. Задержка срабатывания на третьем триггере такая же, как и на
первом. Такой счетчик называется счетчиком с параллельным переносом. Как
видно из схемы, с увеличением числа разрядов увеличивается число лог. элементов И, причем чем выше разряд, тем больше входов у элемента.
Это является недостатком таких счетчиков.
3.2 Тактируемые триггеры
На входы логического элемента или устройства сигналы не всегда поступают одновременно, так как перед этим они могут проходить через разное число элементов с различной задержкой. Это явление описывается как состязание или гонки сигналов. В результате в течении некоторого времени на входах создается непредвиденная ситуация: новые значения одних сигналов сочетаются с предыдущими значениями других, что может привести к ложному срабатыванию элемента (устройства). Последствия гонок можно устранить временным стробированием, когда на элемент, кроме информационных сигналов подаются тактирующие (синхронизирующие) импульсы, к моменту прихода которых информационные сигналы заведомо успевают установиться на входах.
Тактируемый триггер, кроме информационных входов, имеет синхронизирующий (тактирующий, тактовый) вход С; сигналы на информационных входах воздействуют на такой триггер только с поступлением сигнала на синхронизирующий вход. Различают следующие виды тактируемых триггеров: RS-триггеры (рисунок 3.2.1), двухступенчатые RS-триггеры, D-триггеры и JK-триггеры
Рисунок 3.2.1. ТактируемыйRS-триггер.
Реверсивный счетчик
Описанные выше счетчики
однонаправленные и считают на увеличение, однако на практике часто необходимо
менять направление счета в процессе работы. Счетчики, которые в процессе работы
могут менять направление счета называются реверсивными.
Рис. 3 Реверсивный счетчик
Для счетных импульсов
предусмотрены два входа: «+1» — на увеличение, «-1» — на
уменьшение. Соответствующий вход (+1 или -1) подключается ко
входу С. Это можно сделать схемой ИЛИ, если влепить ее перед первым
триггером (выход элемента ко входу первого триггера, входы — к шинам +1 и -1).
Непонятная фигня между
триггерами (DD2 и DD4) называется элементом И-ИЛИ. Этот элемент
составлен из двух элементов И и
одного элемента ИЛИ, объединенных в одном корпусе. Сначала входные сигналы на
этом элементе логически перемножаются, потом результат логически складывается.
Число входов элемента
И-ИЛИ соответствует номеру разряда, т. е. если третий разряд, то три входа,
четвертый — четыре и т. д. Логическая схема является двухпозиционным
переключателем, управляемым прямым или инверсным выходом предыдущего триггера. При лог. 1 на прямом выходе счетчик отсчитывает импульсы с
шины «+1» (если они, конечно, поступает), при лог. 1 на инверсном
выходе — с шины «-1». Элементы И (DD6.1 и
DD6.2) формируют сигналы переноса. На выходе >7 сигнал формируется при коде
111 (число 7) и наличии тактового импульса на шине +1, на выходе <0 сигнал
формируется при коде 000 и наличии тактового импульса на шине -1.
Все это, конечно,
интересно, но красивей смотрится в микросхемном
исполнении:
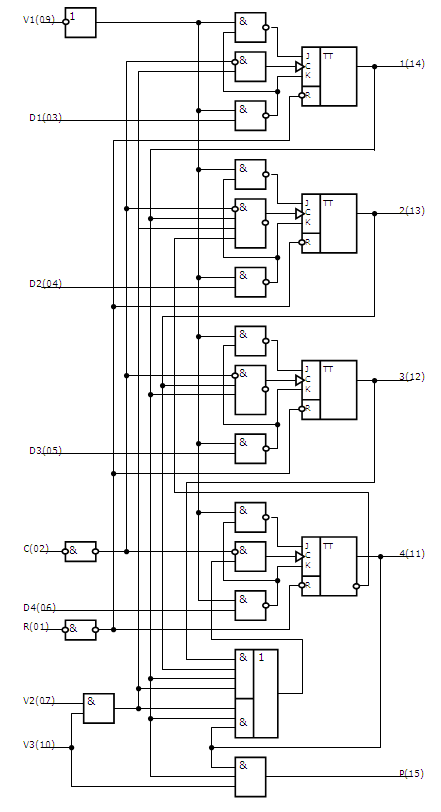
Рис. 4 Четырехразрядный двоичный счетчик
Вот типичный счетчик с предустановкой. СТ2
означает, что счетчик двоичный, если он десятичный, то ставится СТ10,
если двоично-десятичный — СТ2/10. Входы D0 — D3 называются
информационными входами и служат для записи в счетчик какого-либо двоичного
состояния. Это состояние отобразится на его выходах и от него будет производится начало отсчета. Другими словами, это входы предварительной
установки или просто предустановки. Вход V
служит для разрешения записи кода по входам D0 — D3, или, как говорят, разрешения
предустановки. Этот вход может обозначаться и
другими буквами. Предварительная запись в счетчик производится при подаче
сигнала разрешения записи в момент прихода импульса на вход С. Вход С тактовый. Сюда запихивают импульсы. Треугольник означает,
что счетчик срабатывает по спаду импульса. Если треугольник повернут на 180
градусов, т. е. задницей к букве С, значит он
срабатывает по фронту импульса. Вход R служит для обнуления счетчика, т.
е. при подаче импульса на этот вход на всех выходах счетчика устанавливаются
лог. 0. Вход PI называется входом переноса. Выход p
называется выходом переноса. На этом выходе формируется сигнал при переполнении
счетчика (когда на всех выходах устанавливаются лог. 1). Этот сигнал можно
подать на вход переноса следующего счетчика. Тогда при переполнении первого
счетчика второй будет переключаться в следующее состояние. Выходы 1, 2, 4, 8
просто выходы. На них формируется двоичный код, соответствующий числу
поступивших на вход счетчика импульсов. Если выводы с кружочками, что бывает
намного чаще, значит они инверсные, т. е. вместо лог.
1 подается лог. 0 и наоборот. Более подробно работа счетчиков совместно с
другими устройствами будет рассматриваться в дальнейшем.
Счетчики с произвольным порядком пересчета
Построенные на основе D-триггеров
Рис.13 Структурная схема
Рис.14 Счетчик с произвольным порядком пересчета и его граф состояний
Рис.15 Граф состояний
| Q2 | Q1 | Q0 | f2 | f1 | f0 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | |||
| 1 | 1 | ||||
| 1 | 1 | 1 | |||
| 1 | 1 | 1 | |||
| 1 | 1 | 1 |
Каждый разряд булевой функции определяет значение счетчика.
f2=Q2⨁Q1⨁Q{\displaystyle ~f_{2}=Q_{2}\bigoplus Q_{1}\bigoplus Q_{0}} f1=Q2⋅Q¯{\displaystyle ~f_{1}=Q_{2}\cdot {\overline {Q_{0}}}} f=Q2⨁Q1⨁1{\displaystyle ~f_{0}=Q_{2}\bigoplus Q_{1}\bigoplus 1}
Построенные на основе T-триггеров
Рис.16 Структурная схема
Рис.17 Счетчик с произвольным порядком пересчета
| Q2 | Q1 | Q0 | f2 | f1 | f0 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | |||
| 1 | 1 | 1 | |||
| 1 | 1 | ||||
| 1 | 1 | 1 | |||
| 1 | 1 | 1 | 1 |
Булева функция определяет, меняет ли разряд свое значение или сохраняет.
f2=Q1⨁Q∨{\displaystyle ~f_{2}=Q_{1}\bigoplus Q_{0}\vee } f1=Q¯⋅(Q2⨁Q1){\displaystyle ~f_{1}={\overline {Q_{0}}}\cdot (Q_{2}\bigoplus Q_{1})} f=Q2¯{\displaystyle ~f_{0}={\overline {Q_{2}}}}
Рис.18 Граф состояний
Построенные на основе JK-триггеров
Рис.19 Структурная схема
Рис.20 Счетчик с произвольным порядком пересчета и его граф состояний
Рис.21 Граф состояний
| Q2 | Q1 | Q0 | J2 | K2 | J1 | K1 | J0 | K0 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | x | 1 | x | x | |||
| 1 | 1 | x | x | x | 1 | |||
| 1 | x | 1 | x | x | ||||
| 1 | 1 | x | 1 | x | x | |||
| 1 | 1 | x | 1 | 1 | 1 | x |
1 на выходе J — возможность переключения триггера в единичное состояние
1 на выходе K — возможность переключения триггера в нулевое состояние
0 на выходе J — запрет переключения триггера в единичное состояние
0 на выходе K — запрет переключения триггера в нулевое состояние
J2=1 J1=Q¯ J=Q2¯{\displaystyle ~J_{2}=1~J_{1}={\overline {Q_{0}}}~J_{0}={\overline {Q_{2}}}}
K2=Q1∨Q{\displaystyle ~K_{2}=Q_{1}\vee Q_{0}}
K1=Q2¯ K=Q2¯{\displaystyle ~K_{1}={\overline {Q_{2}}}~K_{0}={\overline {Q_{2}}}}
3 Задание к работе
3.1 Исследовать суммирующий счётчик.
Сконфигурировать ПЛИС в соответствии с рисунком 3.1.
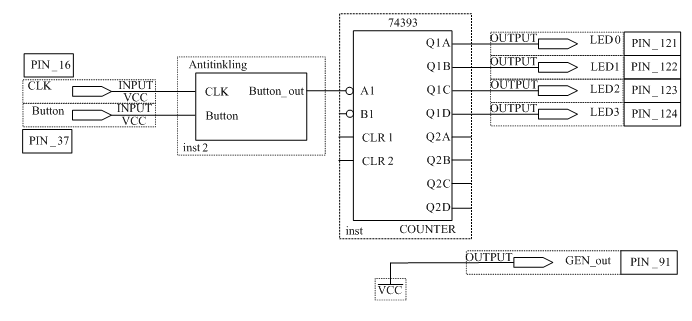
Элемент 74393 представляет собой суммирующий счётчик.
ВНИМАНИЕ! Для того, что бы выполнить блок Antitinkling, прочтите инструкцию Борьба с дребезгом контактов. Подавая с помощью кнопки Button на вход счётчика импульсы и наблюдая за выходами Q, заполнить таблицу 3.1
Подавая с помощью кнопки Button на вход счётчика импульсы и наблюдая за выходами Q, заполнить таблицу 3.1.
Таблица 3.1 – Таблица состояний суммирующего счётчика
| Номер входного импульса | QD | QC | QB | QA |
| 1 | ||||
| … | ||||
| 15 |
3.2 Исследовать вычитающий счётчик.
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.
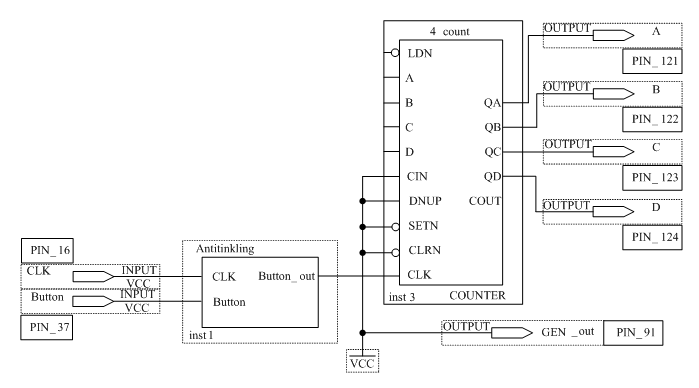
Элемент 4 count представляет собой вычитающий 4-х разрядный счётчик.
Подавая с помощью кнопки Button на вход счётчика импульсы и наблюдая за выходами, заполнить таблицу 3.2.
Таблица 3.2 – Таблица состояний вычитающего счётчика
| Номер входного импульса | QD | QC | QB | QA |
| 1 | ||||
| … | ||||
| 15 |
3.3 Исследовать счётчик с произвольным модулем счёта.
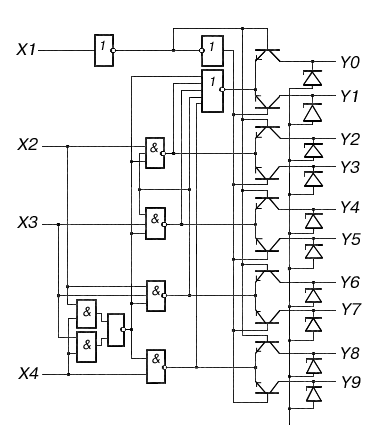
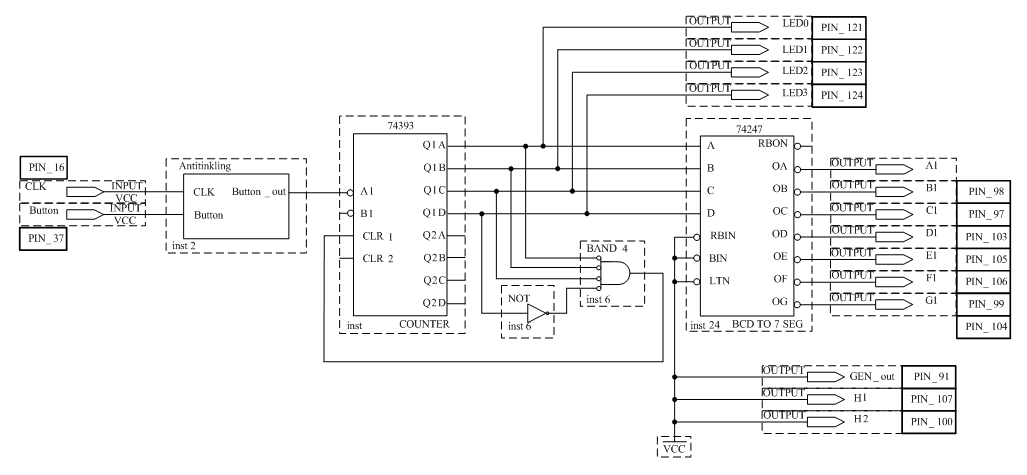
В соответствии с вариантом, полученным у преподавателя, разработать схему счётчика с заданным модулем счёта. В соответствии с разработанной схемой сконфигурировать ПЛИС. На рис 3.3 приведён пример схемы счётчика с модулем счёта 8. К выходам счётчика через преобразователь кодов 74247 подключён семисегментный индикатор.
Подавая с помощью кнопки Button на вход счетчика импульсы и наблюдая за выходами QA, QB, QC, QD и цифровым индикатором, заполнить таблицу 3.3.
Таблица 3.3 – Таблица состояний счётчика с произвольным модулем счёта
| Номер входного импульса | QD | QC | QB | QA | Цифра на индикаторе |
| 1 | |||||
| … | |||||
| 15 |
5.3 Топологическое проектирование
Результаты топологического проектирования вентилей в Microwind:
Рисунок 5.3.1 Топология инвертора
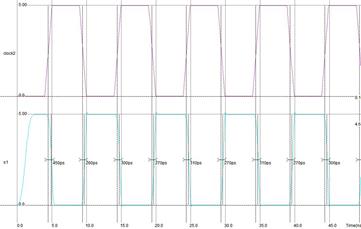
Рисунок 5.3.2. Диаграмма переключения инвертора (частота 100МГц).
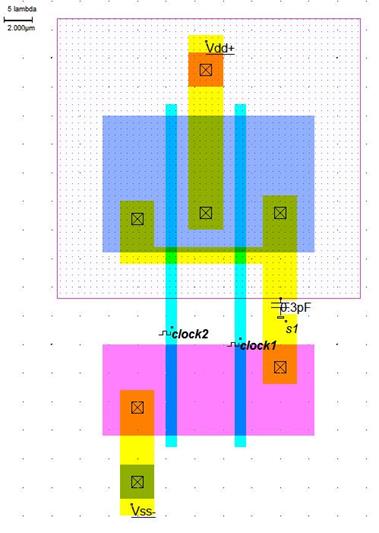
Рисунок 5.3.3. Топология элемента «2и-не».
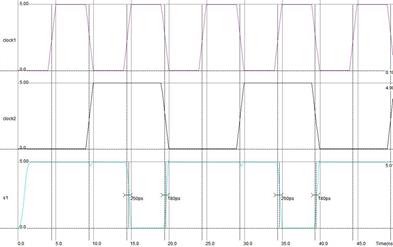
Рисунок 5.3.4. Диаграмма переключения элемента «2и-не» (частота 100МГц).
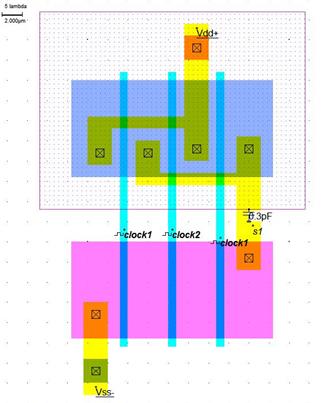
Рисунок 5.3.5. Топология элемента «3и-не»
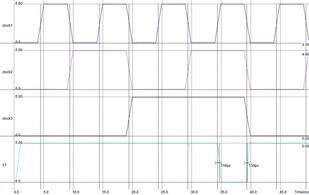
Рисунок 5.3.6. Диаграмма переключения элемента «3и-не» (частота 100МГц).
Таблица 5.2.1. Результаты топологического моделирования вентилей
| t10зд , нс |
t01зд , нс |
tсрзд , нс |
tср , нс |
tфр , нс |
|
| НЕ | 0,300 | 0,270 | 0,285 | 0,490 | 0,460 |
| 2И-НЕ | 0,260 | 0,180 | 0,220 | 0,520 | 0,470 |
| 3И-НЕ | 0,310 | 0,130 | 0,220 | 0,520 | 0,480 |
6.
TV-триггер
Вычитающий счетчик
|
Прохождение сигналов через триггеры счетчика. |
Вычитающие счетчики ( их еще называют счетчиками обратного счета) отличаются от суммирующих тем, что счетные входы каждого из последующих триггеров присоединяются не к прямому выходу предыдущего триггера, а к инверсному Q. Вторая особенность состоит в том, что в исходном состоянии все разряды или часть разрядов заполняется не нулями, а единицами уменьшаемого числа. При поступлении на вход импульсов, которые надо вычесть из заранее установленного числа, триггеры, начиная с первого, последовательно срабатывают и уменьшают установленное число.
|
Временная диаграмма асинхронного суммирующего счетчика. |
Асинхронные вычитающие счетчики строятся аналогично суммирующим счетчикам. Аналогично, схема на рис. 8.41, б преобразуется в схему вычитающего счетчика, если входы разрядов аъ Ьг, а2, Ьг подключить к выходам s2, s2, ss, s3 соответственно.
Отдельно вычитающие счетчики используются редко: операция вычитания организуется вместе со сложением в схемах реверсивных счетчиков. В ряде случаев работа счетчика начинается с произвольного числа, занесенного в счетчик в параллельном двоичном коде. В рассмотренных схемах ( рис. 9 — 5, 9 — 6) единица переноса из разряда в разряд передается последовательно.
Строится вычитающий счетчик так же, как суммирующий, но с тем отличием, что со входом каждого последующего триггера соединяется другой выход предыдущего триггера.
|
Вычитающий счетчик.| Реверсивный счетчик. |
Работа вычитающего счетчика происходит следующим образом.
В вычитающем счетчике поступление на вход очередной логической единицы ( очередного импульса) вызывает уменьшение хранившегося в счетчике числа на единицу. Он отличается от суммирующих счетчиков тем, что счетные входы каждого из последующих триггеров подсоединены не к прямому выходу предыдущего триггера, а к инверсному. Кроме того, в исходном состоянии все разряды ( или часть из них) заполняются не нулями, а единицами уменьшаемого числа. При поступлении на вход импульсов, которые надо вычесть из заранее установленного числа, триггеры, начиная с первого, последовательно срабатывают и уменьшают это число. На рис. 1.25 представлена схема вычитающего счетчика с последовательной передачей переносов. Как и суммирующий счетчик, вычитающий имеет период циклической работы, равный 2 импульсов.
|
Структурная схема двоичного.| Структурная схема регистра сдвига. |
В вычитающем счетчике перенос снимается не с нулевого, а с единичного выхода триггера. В реверсивном счетчике, в зависимости от режима, цепи переноса переключаются.
В вычитающем счетчике сигнал на счетный вход поступает с выхода Q предыдущего триггера, а не с выхода Q.
Электронный двоичный вычитающий счетчик. Вычитание производится с помощью таких же триггеров, как и в предыдущем случае, с тем отличием, что соединение их произведено несколько по-иному. Здесь выход каждого триггера берется с анода второй лампы и присоединяется, как и в предыдущем случае, к сетке первой лампы следующего триггера.
Пусть асинхронный вычитающий счетчик ( из задания 7) циклического типа.
|
Трехразрядный асинхронный счетчик. а — логическая структура. б — временная диаграмма. |
Двоичные асинхронные счётчики
Простейший вид счётчика — двоичный может быть построен на основе T-триггера. T-триггер изменяет своё состояние на прямо противоположное при поступлении на его вход синхронизации импульсов. Для реализации T-триггера воспользуемся универсальным D-триггером с обратной связью, как это показано на рисунке 1.
Рисунок 1. Реализация счетного T-триггера на универсальном D-триггере
Так как схема T-триггера при поступлении на вход импульсов меняет свое состояние на противоположное, то её можно рассматривать как счётчик, считающий до двух. Временные диаграммы сигналов на входе и выходах T-триггера приведены на рисунке 2.
Рисунок 2 Временные диаграммы сигналов на входе и выходах T-триггера
Обычно требуется посчитать большее количество импульсов. В этом случае можно использовать выходной сигнал первого счетного триггера как входной сигнал для следующего триггера, то есть соединить триггеры последовательно. Так можно построить любой счётчик, считающий до максимального числа, кратного степени два. Такой счетчик называется двоичным счетчиком, а тот факт, что состояние триггеров меняется на противоположное в различные моменты времени по мере распространения цифрового сигнала, отображается термином: асинхронный двоичный счетчик.
Схема счётчика, позволяющего посчитать любое количество импульсов, меньшее шестнадцати, приведена на рисунке 3. Количество поступивших на вход импульсов можно узнать, подключившись к выходам счётчика . Это число будет представлено в двоичном коде.
Рисунок 3. Схема четырёхразрядного счётчика, построенного на универсальных D-триггерах
Для того чтобы разобраться, как работает схема двоичного счётчика, воспользуемся временными диаграммами сигналов на входе и выходах этой схемы, приведёнными на рисунке 4.
Рисунок 4 Временная диаграмма четырёхразрядного счётчика
Пусть первоначальное состояние всех триггеров счётчика будет нулевым. Это состояние мы видим на временных диаграммах. Запишем его в таблицу 1. После поступления на вход счётчика тактового импульса (который воспринимается по заднему фронту) первый триггер изменяет своё состояние на противоположное, то есть единицу.
Запишем новое состояние выходов счётчика в ту же самую таблицу. Так как по приходу первого импульса изменилось состояние первого триггера, то этот триггер содержит младший разряд двоичного числа (единицы). В таблице поместим его значение на самом правом месте, как это принято при записи любых многоразрядных чисел. Здесь мы впервые сталкиваемся с противоречием правил записи чисел и правил распространения сигналов на принципиальных схемах.
Подадим на вход счётчика ещё один тактовый импульс. Значение первого триггера снова изменится на прямо противоположное. На этот раз на выходе первого триггера, а значит и на входе второго триггера сформируется задний фронт. Это означает, что второй триггер тоже изменит своё состояние на противоположное. Это отчётливо видно на временных диаграммах, приведённых на рисунке 4. Запишем новое состояние выходов счётчика в таблицу 1. В этой строке таблицы образовалось двоичное число 2. Оно совпадает с номером входного импульса.
Продолжая анализировать временную диаграмму, можно определить, что на выходах приведённой схемы счётчика последовательно появляются цифры от 0 до 15. Эти цифры записаны в двоичном виде. При поступлении на счётный вход счётчика очередного импульса, содержимое его триггеров увеличивается на 1. Поэтому такие счётчики получили название суммирующих двоичных счётчиков.
Таблица 1. Изменение уровней на выходе суммирующего счётчика при поступлении на его вход импульсов.
| номер входного импульса | Q3 | Q2 | Q1 | Q0 |
| 1 | 1 | |||
| 2 | 1 | |||
| 3 | 1 | 1 | ||
| 4 | 1 | |||
| 5 | 1 | 1 | ||
| 6 | 1 | 1 | ||
| 7 | 1 | 1 | 1 | |
| 8 | 1 | |||
| 9 | 1 | 1 | ||
| 10 | 1 | 1 | ||
| 11 | 1 | 1 | 1 | |
| 12 | 1 | 1 | ||
| 13 | 1 | 1 | 1 | |
| 14 | 1 | 1 | 1 | |
| 15 | 1 | 1 | 1 | 1 |
Условно-графическое обозначение суммирующего двоичного счетчика на принципиальных схемах приведено на рисунке 5. В двоичных счётчиках обычно предусматривают вход обнуления микросхемы R, который позволяет записать во все триггеры счётчика нулевое значение. Это состояние иногда называют исходным состоянием счётчика.
Рисунок 5. Четырёхразрядный двоичный счётчик
Существуют готовые микросхемы асинхронных двоичных счётчиков. Классическим примером такого счётчика является микросхема 555ИЕ5. Подобные схемы существуют и внутри САПР программируемых логических интегральных схем.
4.1 Моделирование TV-триггера
триггер суммирующий счетчик
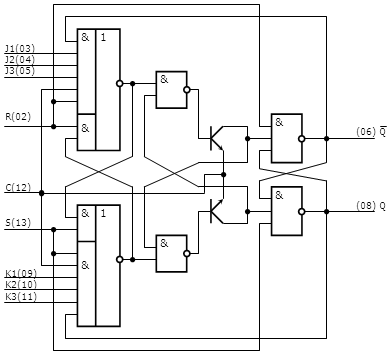
По заданию, необходимо использовать динамический TV-триггер, в качестве базисного. Для этого, модифицируем схему стандартного динамического JK триггера, превратив его в T-триггер, и добавив ему асинхронные входа R и V (сброс и принудительное хранение). В итоге, собранный триггер будет выглядеть следующим образом:
Рисунок 4.1.1. Динамический TV-триггер.
Проведем логическое моделирование TV-триггера в Orcad:
Рисунок 4.1.2. Схема TV-триггера в Orcad.
Результат логического моделирования:
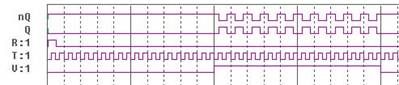
Рисунок 4.2.3. Диаграмма переключения TV-триггера.
Таблица 4.1.1. Таблица истинности TV-триггера.
| V | T | Qn+1 |
| Qn | ||
| 1 | Qn | |
| 1 | Qn | |
| 1 | 1 | ⌐ Qn |
3.5 Счетчики с последовательным переносом
Первый разряд счетчика, будучи счетным триггером, переключается каждым входным импульсом. Каждый последующий разряд счетчика получает переключающий перепад (1/0 или 0/1) от предыдущего разряда – переключающий перепад распространяется вдоль цепочки триггеров счетчика последовательно.
Схема суммирующего счетчика с последовательным переносом приведена на рисунке 3.5.1, а. С поступлением каждого входного импульса число в счетчике увеличивается на единицу. Если в данном разряде присутствует единица, то под воздействием перепада, поступающего от предшествующего, он обнуляется, и единица переносится в следующий разряд. Если же в данном разряде ноль, то в него вписывается единица.
Рисунок 3.5.1. Суммирующий счетчик с последовательным переносом а) схема, б) условное изображение.
На рисунке 3.5.2, б представлено условное изображение 4-разрядного счетчика. На счетный С вход поступают импульсы. Логическая единица на входе К сбрасывает все разряды счетчика в ноль. По входам предварительной установки D
– D3
в счетчик может быть записано число, его значение должно сопровождаться логической единицей на входе разрешения V. Число, занесенное в счетчик, фиксируется на его выходах двоичным кодом с «весами» разрядов 1-2-4-8. На выходе P+
появляется логическая единица с поступлением на вход 16-го импульса, т. е. вслед за тем, как предыдущими 15-ю импульсами все разряды счетчика были установлены в единицу.
Суммирующий счетчик функционирует по правилам сложения двоичных чисел. Это легко проследить по временной диаграмме, изображенной на рисунке 3.5.2, где крестиками отмечены переключающие перепады 1/0.
Рисунок 3.5.2. Временная диаграмма работы суммирующего счетчика.
Из временных диаграмм можно сделать следующие выводы:
— с наибольшей частотой переключается входной триггер счетчика;
— частота импульсов на выходе каждого триггера вдвое меньше, частоты импульсов на его входе, а nразрядов счетчика делят частоту входных импульсов в 2n
раз, таким образом, счетчик является делителем числа входных импульсов с коэффициентом деления (пересчета), равным емкости счетчика Ксч
;
— при поступлении на вход суммирующего счетчика 2n
импульсов он переполняется: все триггеры устанавливаются в 0 (счетчик обнуляется);
— максимальное число, которое может содержать счетчик, на единицу меньше его емкости N = Ксч
– 1 = 2n
– 1;
— в момент, предшествующий переключению очередного разряда, все предыдущие разряды счетчика находятся в состоянии 1.
Если в счетчике использованы триггеры, переключающиеся перепадом 0/1, то вход последующего триггера нужно соединить с инверсным выходом предыдущего, на котором формируется этот перепад, когда по основному выходу триггер переключается из 1 в 0.
Принцип работы операционного усилителя
Давайте рассмотрим, как работает ОУ
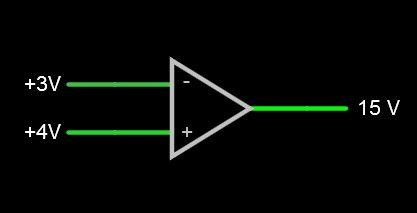
Принцип работы ОУ очень прост. Он сравнивает два напряжения и на выходе уже выдает отрицательный, либо положительный потенциал питания. Все зависит от того, на каком входе потенциал больше. Если потенциал на НЕинвертирующем входе U1 больше, чем на инвертирующем U2, то на выходе будет +Uпит, если же на инвертирующем входе U2 потенциал будет больше, чем на НЕинвертирующем U1, то на выходе будет -Uпит. Вот и весь принцип ;-).
Давайте рассмотрим этот принцип в симуляторе Proteus. Для этого выберем самый простой и распространенный операционный усилитель LM358 (аналоги 1040УД1, 1053УД2, 1401УД5) и соберем примитивную схему, показывающую принцип работы

Подадим на НЕинвертирующий вход 2 Вольта, а на инвертирующий вход 1 Вольт. Так как на НЕинвертирующем входе потенциал больше, то следовательно, на выходе мы должны получить +Uпит. Мы получили 13,5 Вольт, что близко к этому значению

Но почему не 15 Вольт? Виновата во всем сама внутренняя схемотехника ОУ. Максимальное значение ОУ не всегда может равняться положительному либо отрицательному напряжению питания. Оно может отклоняться от 0,5 и до 1,5 Вольт в зависимости от типа ОУ.
Но, как говорится, в семье не без уродов, и поэтому на рынке уже давно появились ОУ, которые могут выдавать на выходе допустимое напряжение питания, то есть в нашем случае это значения, близкие к +15 и -15 Вольтам. Такая фишка называется Rail-to-Rail, что в дословном переводе с англ. “от рельса до рельса”, а на языке электроники “от одной шины питания и до другой”.
Давайте теперь на инвертирующий вход подадим потенциал больше, чем на НЕинвертирущий. На инвертирующий подаем 2 Вольта, а на НЕинвертирующий подаем 1 Вольт:

Как вы видите, в данный момент выход “лег” на -Uпит, так как на инвертирующем входе потенциал был больше, чем на НЕинвертирующем.
Чтобы не качать лишний раз программный комплекс Proteus, можно в онлайне с помощью программы Falstad сэмулировать работу идеального ОУ. Для этого выбираем вкладку Circuits—Op-Amps—>OpAmp. В результате на вашем экране появится вот такая схемка:
На правой панели управления увидите бегунки для добавления напряжения на входы ОУ и уже можете визуально увидеть, что получится на выходе ОУ при изменении напряжения на входах.