Спектр сигнала

Компоненты для ряда Фурье

Другим фактором, определяющим профиль рассматриваемой системы конкретной формы волны, является функция, которая должна быть выявлена, как нечетная или четная. Вторая – это та, в которой f (t) = f (–t), а для первой –f (t) = f (–t). В четной функции присутствуют только косинусные гармоники. Поэтому синусные амплитудные коэффициенты bn равны нулю. Аналогично, в нечетной функции присутствуют только синусоидальные гармоники. Поэтому косинусные амплитудные коэффициенты равны нулю.

Как симметрия, так и противоположные значения могут проявляться несколькими способами в форме волны. Все эти факторы способны влиять на характер рядов Фурье вида зыби. Или, в терминах уравнения, член ao отличен от нуля. Компонент постоянного тока представляет собой случай асимметрии спектра сигнала. Это смещение может серьезно повлиять на измерительные электронные схемы, которые связаны по неменяющемуся напряжению.

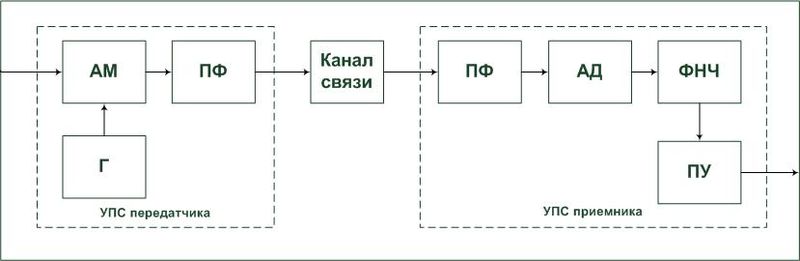
Передача электрических сигналов

Итак, для передачи сигнала через пространство мы будем использовать провода. Чуть выше мы разобрали условия возникновения сигнала. Значит, первым делом, нам нужен генератор этих сигналов! То есть это может быть какая-либо батарея или схемка, которая бы генерировала  электрический ток. Далее, должен быть кто-то, кто бы принимал этот сигнал. Это может быть какая-нибудь нагрузка, типа лампочки, нагревательного элемента или целой схемы, которая бы принимала этот сигнал. Ну и в-третьих, нагрузка должна как-то среагировать на этот сигнал. Лампочка должна источать свет, нагревательный элемент – греться, а схема исполнять какую-либо функцию.

Как вы поняли из всего выше сказанного, главный козырь сигнала – это его генератор. Итак, как мы уже разобрали, по проводам можно передавать два параметра электрического тока – это напряжение и сила тока. То есть мы можем создать  генератор, который бы менял или свое напряжение или силу тока в нагрузке, которая бы цеплялась через провода к этому генератору. В основном в электронике используют именно параметр “напряжение”, так как напряжение легко получить и менять его значение.

Математическое представление

Спектр периодического сигнала s(t){\displaystyle s(t)} имеет вид:

Cn=1T∫Ts(t)e−inω1tdt{\displaystyle C_{n}={\frac {1}{T}}\int \limits _{0}^{T}s(t)e^{-in\omega _{1}t}dt}, где T{\displaystyle T} — период сигнала s(t){\displaystyle s(t)}, ω1=2πT{\displaystyle \omega _{1}=2\pi /T}, n{\displaystyle n} — целое.

Спектр непериодического сигнала s(t){\displaystyle s(t)} можно записать через преобразование Фурье (можно без коэффициента 12π{\displaystyle 1/{\sqrt {2\pi }}}) в виде:

S(ω)=∫−∞+∞s(t)e−iωtdt{\displaystyle S(\omega )=\int \limits _{-\infty }^{+\infty }s(t)e^{-i\omega t}dt}, где ω{\displaystyle \omega } — угловая частота, равная 2πf{\displaystyle 2\pi f}.

Спектр сигнала является комплексной величиной и представляется в виде:
S(ω)=A(ω)e−iϕ(ω){\displaystyle S(\omega )=A(\omega )e^{-i\phi (\omega )}}, где A(ω){\displaystyle A(\omega )} — амплитудный спектр сигнала, ϕ(ω){\displaystyle \phi (\omega )} — фазовый спектр сигнала.

Если под сигналом s(t){\displaystyle s(t)} понимать электрическое напряжение на резисторе сопротивлением 1 Ом, то энергия сигнала, выделяемая на этом резисторе на интервале времени (, T){\displaystyle (0,\ T)}, будет равна E=∫Ts2(t)dt{\displaystyle E=\int \limits _{0}^{T}s^{2}(t)dt}, средняя мощность — W=1T∫Ts2(t)dt{\displaystyle W={\frac {1}{T}}\int \limits _{0}^{T}s^{2}(t)dt}.

9.4. Спектры типовых сигналов

Определим спектры наиболее распространенных типов электрических сигналов.

Единичная функция задается уравнением (7.19) (см. рис. 7.2, а). Строго говоря, функция (7.19) не удовлетворяет условию абсолютной интегрируемости, поэтому воспользуемся следующим приемом: умножим 1(t) на «гасящий» множитель е–ct(с = const). При этом можно использовать прямое преобразование Фурье (9.6):

Преобразование F(jw, c) носит название обобщенного преобразования Фурье. Для получения спектра единичной функции перейдем к пределу:

Из уравнения (9.38) получаем амплитудный |F(jw)| = 1/w (рис. 9.4, а) и фазовый спектр функции j(w) (рис. 9.4, б): j(w) = = —p/2, т. е. амплитудный спектр при w = 0 обращается в бесконечность, что свидетельствует о наличии в исходной функции 1(t) скачка при t = 0 (см. рис. 7.2, а). Для образования этого скачка в соответствии с (9.38) при t = 0 осуществляется суммирование бесконечно большого числа синусоидальных составляющих. Спектр (9.38) может быть получен и с помощью изображения единичной функции (7.20):

Единичная импульсная функция. Функция d(t) задается аналитически условиями (7.21). Для нахождения спектра d-функции воспользуемся прямым преобразованием Фурье (9.6), которое с учетом (9.8)—(9.10) можно записать в виде

Так как второе слагаемое равно нулю, а первое — единице вследствие свойств (7.21)—(7.23), то окончательно получим

Таким образом, d-функция имеет равномерный амплитудный и нулевой фазовый спектры. Равенство нулю на всех частотах фазового спектра означает, что все гармонические составляющие d-функции, суммируясь с нулевыми начальными фазами, образуют при t = 0 пик бесконечно большого значения.

Следует отметить, что сдвиг d-функции на время t приводит согласно свойствам преобразования Фурье к спектру , т. е. амплитудный спектр функции d(t—t) остается прежним, а фазовый изменяется пропорционально wt.

Из равенства (9.39) согласно обратному преобразованию Фурье (9.7) следует, что

Учитывая условие взаимозаменяемости параметров t и w, последнее выражение можно переписать в следующем виде:

Уравнения (9.40) и (9.41) широко используются в теории сигналов и цепей.

Спектр постоянной составляющей функции a/2 = 1/2 с учетом (9.41) определяется уравнением

Таким образом, спектр постоянной составляющей равен нулю на всех частотах, кроме w = 0, где F(jw) обращается в бесконечность, то есть имеем на частоте w = 0 дискретную составляющую частоты в форме d-функции.

Спектр гармонического колебания. Проиллюстрируем методику использования прямого преобразования Фурье при определении спектра гармонического колебания

Преобразование (9.6) для функции (9.43) имеет вид

Формально функция (9.43) не удовлетворяет условию абсолютной интегрируемости, так как имеет показатель роста с = 0. По этому для вычисления интеграла (9.44) воспользуемся формулой Эйлера (3.18) и уравнением (9.41):

т. е. гармоническое колебание имеет дискретный спектр, состоящий из двух спектральных линий на частотах ±w.

Спектр одиночного прямоугольного импульса (см. рис. 9.2) можно найти как непосредственно из прямого преобразования Фурье (9.6), так и путем предельного перехода при q  ¥ (T ¥) в разложении (5.27). В результате получим

На рис. 9.3 изображен спектр одиночного импульса. Сравнение рис. 9.3 и рис. 9.4 показывает, что по своей форме спектр одиночного импульса совпадает с огибающей дискретного спектра последовательности периодических импульсов, однако спектр одиночного импульса является сплошным.

Из условия взаимосвязи между частотными и временными характеристиками сигнала следует, что сигнал с ограниченным по частоте ±w спектром прямоугольной формы (рис. 9.5, а) имеет бесконечную протяженность и форму, аналогичную спектру прямоугольного импульса (рис. 9.5, б).

Спектр радиоимпульса (рис. 9.6) можно найти как произведение видеоимпульса прямоугольной формы (рис. 9.7) и гармонического колебания (9.43). Тогда, воспользовавшись теоремой свертки (9.30), получим:

На рис. 9.8 показан вид спектра радиоимпульса.

Аналогичным образом можно найти спектр сигналов и более сложной формы.

Пример. Найти спектр экспоненциального импульса

В соответствии с прямым преобразованием (9.6) получаем

где — амплитудный (рис. 9.9, а) и —фазовый (рис. 9.9, б) спектры сигнала.

Пример 2. Определить спектр затухающего колебания (рис. 9.10)

Согласно (9.6) находим

Отсюда находим спектры:

амплитудный (рис. 9.11, а)

и фазовый (рис. 9.11, б)

В таблице 9.1 приведены спектры некоторых наиболее распространенных сигналов.

Определение практической ширины спектра сигнала

Ограничение практической ширины спектра сигнала по верхнему значению частоты , по заданному энергетическому критерию осуществляется на основе неравенства:

где — энергия сигнала с ограниченным вверху спектром.

Значение определяется на основе известной плотности:

где — искомое значение верхней граничной частоты сигнала.

А также определяется по формуле

Значение определяется путём подбора при расчётах на ЭВМ пользуясь формулами (2.6) и (2.5).

Найдём и для каждого из сигналов , , , учитывая (1.9), (1.11), (1.13):

Третий сигнал имеет меньшую граничную частоту , следовательно, его и выбираем для дальнейшего анализа и расчёта.

Анализатор спектра сигнала

Процесс выборки аналогичен форме амплитудной модуляции, в которой V (t) является построенным оповещением со спектром от постоянного тока до Fm, а p (t) — несущей частотой. Полученный результат напоминает двойную боковую полосу с несущей величиной АМ. Спектры сигналов модуляции появляется вокруг частоты Fo. Фактическая величина немного сложнее. Подобно нефильтрованному радиопередатчику AM, она появляется не только вокруг основной частоты (Fs) несущей, но также и на гармониках, расположенных с интервалами Fs вверх и вниз.

При условии, что частота дискретизации соответствует уравнению Fs ≥ 2Fm, исходный отклик восстанавливается из выборочной версии, передавая его через фильтр нижних колебаний с меняющейся отсечкой Fc. При этом возможно передавать только спектр аналогового звука.

В случае неравенства Fs <2Fm возникает проблема. Это означает, что спектр частотного сигнала похож на предыдущий. Но разделы вокруг каждой гармоники перекрываются так, что «–Fm» для одной системы меньше «+Fm» для следующей более низкой области колебаний. Это перекрытие приводит к дискретизированному сигналу, ширина спектра которого восстанавливается фильтрацией нижних частот. Он будет генерировать не исходную частоту синусоидальной волны Fo, а более низкую, равную (Fs – Fo), и информация, переносимая в форме волны, теряется или искажается.

Расчёт спектра сигнала

Под спектром непериодического сигнала понимают функцию частоты , которую получают на основе прямого преобразования Фурье вида:

Модуль спектральной функции

называют спектром сигнала или спектральной плотностью сигнала.

Аналитическая запись задаваемых сигналов во временной области имеет вид:

Колоколообразный сигнал рис. 1.1

Колоколообразный затухающий сигнал рис 1.2.

Экспоненциальный сигнал рис 1.3.

Определим спектральную плотность для каждого сигала, подставив формулу Эйлера:

в (1.1), получим преобразование Фурье вида:

Запишем спектральную функцию для сигнала . По формуле (1.7), получим:

Модуль спектральной плотности:

Фазовая характеристика в данном случае отсутствует , так как функция чётная (см. свойства интегралов чётных и нечётных функций).

График спектра сигнала представлен на рис 1.4.

Определим спектр сигнала по формуле (1.7), учитывая свойства интегралов от чётных и нечётных функций, т.е. , получим:

Фазовая характеристика в данном случае отсутствует , так как функция чётная (см. свойства интегралов чётных и нечётных функций).

График спектра сигнала представлен на рис. 1.5

Запишем спектральную функцию для сигнала . По формуле (1.7), учитывая свойства интегралов от чётных и нечётных функций, т.е. , получим

Таким образом, модуль спектральной плотности третьего сигнала

Фазовая характеристика в данном случае отсутствует , так как функция чётная (см. свойства интегралов чётных и нечётных функций).

График спектра сигнала представлен на рис. 1.6

Применение

Разложение сигнала в спектр применяется в анализе прохождения сигналов через электрические цепи (спектральный метод). Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал. Одним из преимуществ разложения сигнала в спектр является следующее: сигнал, проходя по цепи, претерпевает изменения (усиление, задержка, модулирование, детектирование, изменение фазы, ограничение и т. д.). Токи и напряжения в цепи под действием сигнала описываются дифференциальными уравнениями, соответствующими элементам цепи и способу их соединения. Линейные цепи описываются линейными дифференциальными уравнениями, причём для линейных цепей верен принцип суперпозиции: действие на систему сложного сигнала, который состоит из суммы простых сигналов, равно сумме действий от каждого составляющего сигнала в отдельности. Это позволяет при известной реакции системы на какой-либо простой сигнал, например, на синусоидальное колебание с определённой частотой, определить реакцию системы на любой сложный сигнал, разложив его в ряд по синусоидальным колебаниям.

На практике спектр измеряют при помощи специальных приборов: анализаторов спектра.

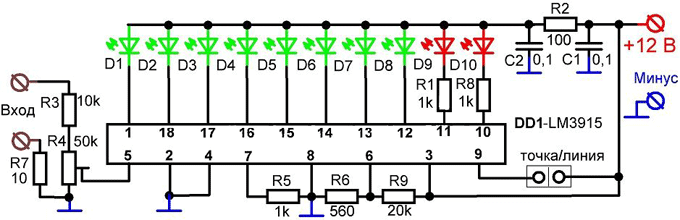
Принцип действия

Для формирования прямоугольного колебания в устройствах-модуляторах имеется специальная микросхема-контроллер либо аналоговая микросхема. Подключение происходит посредством цепи на полупроводнике. Полупроводник имеет только два состояния:

• Закрытое
• Открытое.

Важно! Работа всей цепи зависит от характера колебаний. Следовательно, если лампа подключена через полупроводниковый прибор, она начнёт мерцать с заданной частотой

Однако, когда частота превышает 50 Гц, из-за особенностей глаз человека, мигание сливается в единое свечение. Но таким образом можно регулировать и яркость свечения. Снижение коэффициента повлечет за собой уменьшение яркости света, выдаваемой лампой.

Подобную схему можно использовать для постоянных двигателей. Уменьшение частоты провоцирует снижение скорости вращения двигателя, а высокие – к большей мощности агрегата.

В аналогичных устройствах применяется полупроводниковый переключатель, который имеет высокую скорость срабатывания и низкую проводимость, поскольку в противном случае устройство может запаздывать.

3.1. Аналитическое представление модулированных колебаний

Модулированные сигналы различаются по виду переносчика (несущей) и по его модулированным параметрам. В качестве переносчиков в настоящее время широко используются гармонические колебания, периодическая последовательность импульсов и узкополосный случайный процесс. Каждый из этих переносчиков характеризуется определенным числом параметров. Параметры, изменяющиеся во времени под действием передаваемого сообщения, называются информационными, так как в их изменениях заложена передаваемая информация. Параметры, которые остаются неизменными, являются постоянными признаками сигнала; они могут быть использованы на приеме для отличения сигнала от помех. Во многих случаях модулированный сигнал можно представить как произведение двух функций

                                                                                                  (3.1)

где  — функция, представляющая несущее колебание (переносчик), а — модуляционная функция, выражающая воздействие передаваемого сообщения u(t) на несущую f(t). Когда для представления несущей выбирается аналитический сигнал (2.98), то для каждой модуляционной функции M(t) существует комплексный модулированный сигнал s(t). При аналитическом представлении сигнала его действительная и мнимая части соответствуют реально существующему модулированному сигналу, а его модуль определяет огибающую. В случае, когда несущей является гармоническое колебание , модуляционная функция выражает воздействие видеосигнала u(t) на амплитуду (частоту или фазу) несущей.

Спектр модулированного колебания (3.1) согласно теореме о спектре произведения определяется сверткой

(3.2)

Отсюда следует, что процесс модуляции приводит к сложному преобразованию спектра сигнала. Если несущая представляет собой узкополосное колебание, то модуляция приводит к расширению спектра и переносу его в область около несущей частоты (рис. 3.1 а). Если несущая — чистая синусоида, то имеет место простое смещение спектра (рис. 3.1 б). Если несущая записывается в форме аналитического сигнала, спектр которого существует только для положительных частот, то частотное преобразование относится только к положительным частотам, как показано на рис. 3.1.

Рис. 3.1. Смещение спектра при модуляции: общий случай аналитической несущей (а), случай гармонической несущей (б)

Прямоугольные сигналы в радиотехнике и электронике[ | код]

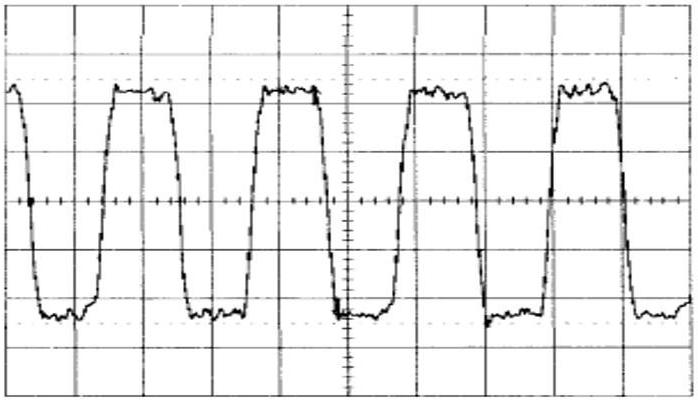
Истинный меандр с нулевой длительностью фронтов физически нереализуем

В радиотехнике и электронике меандром обычно называют сигналы со скважностью 2 и длительностями фронтов много меньших периода повторения сигнала.. Сигнал приближённо такого вида (с ненулевой длительностью фронтов и спадов) генерируется различными автогенераторами, например, мультивибраторами, выполненными на транзисторах, логических элементах, операционных усилителях)

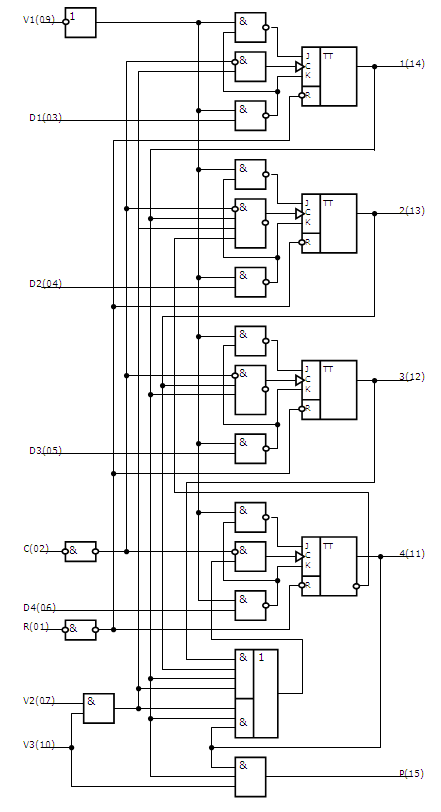
Также сигналы такого типа обычно присутствуют практически во всех цифровых схемах, например, двоичный триггер со счетным входом, переключаемый периодическими импульсами даёт на выходе меандр.

Сигнал приближённо такого вида (с ненулевой длительностью фронтов и спадов) генерируется различными автогенераторами, например, мультивибраторами, выполненными на транзисторах, логических элементах, операционных усилителях). Также сигналы такого типа обычно присутствуют практически во всех цифровых схемах, например, двоичный триггер со счетным входом, переключаемый периодическими импульсами даёт на выходе меандр.