Аппроксимация функции одной переменной

Содержание:

Derivation of formulas
Метод — кусочно-линейная аппроксимация
Построение графика функции
Примеры
Аппроксимация с фиксированной точкой пересечения с осью y
Аппроксимация линейной функцией

Derivation of formulas

Let’s start from the problem:
We have unknown function y=f(x), given in form of table data (for example, those obtained from experiments).
We need to find function with known type (linear, quadratic, etc.) y=F(x), those values should be s close as possible to the table values at same points. On practice, type of function is determined by visually comparing table points to graphs of known functions.

As result we should get a formula y=F(x), named empirical formula (regression equatuion, function approximation), which allows to calculate y for x’s not present in table. Thus, empirical formula «smoothes» y values.

We use Least Squares Method to obtain parameters of F for best fit. The best fit in the least-squares method sense minimizes the sum of squared residuals, a residual being the difference between an observed value and the fitted value provided by a model.

Thus, we need to find function F, such as the sum of squared residuals S will be minimal

Let’s describe solution for this problem using linear regression F=ax+b as example.
We need to find best fit for a and b coefficients, thus
S is function of a and b. To find the minimum we will find extremum points, where partial derivatives equal to zero.

Using formula for derivative of complex function we will get the following equations

For function partial derivatives are,

Expanding first formulas with partial derivatives we will get the following equations

After removing the brackets we will get the following

From these equations we can get formulas for a and b, which will be the same as formulas listed above.

Using the same technique we can get formulas for all remaining regressions

Метод — кусочно-линейная аппроксимация

Визуальная линейная аппроксимация с помощью gnuplot

Метод кусочно-линейной аппроксимации заключается в замене заданной нелинейной характеристики ломаной прямой с одной или несколькими точками излома. Такая замена нелинейной характеристики позволяет вести расчет аналитически с помощью линейных уравнений. Для прямолинейных участков записываются линейные уравнения, решения которых припасовываются: электрические величины для конца участка приравниваются соответствующим величинам для начала следующего участка.

Метод кусочно-линейной аппроксимации основан на замене кривой W ( t) ломаной прямой, приводящей к замене нелинейного уравнения системой линейных уравнений для прямолинейных участков этой ломаной прямой.

Типы импульсных звеньев.

Метод кусочно-линейной аппроксимации заключается в аппроксимации нелинейной характеристики несколькими линейными; для каждого линейного участка составляется линейная математическая модель. В дальнейшем полученные для каждого участка решения соединяются и исследование процесса регулирования производится по общему решению.

Метод кусочно-линейной аппроксимации применим для расчета как установившихся, так и переходных режимов, при этом схемы могут содержать кроме диодов и другие полупроводниковые приборы, характеристики которых также соответствующим образом линеаризованы.

Метод трех ординат.

Метод кусочно-линейной аппроксимации заключается в замене заданной нелинейной характеристики ломаной прямой с одной или несколькими точками излома.

Метод кусочно-линейной аппроксимации при решении задач моделирования и восстановления измерительных сигналов занимает особое положение. Сравнительно простая процедура аппроксимации, легко реализуемая современными средствами дискретной микроэлектроники, высокая точность, приемлемая для большинства операций по функциональной обработке измерительных сигналов, делают его универсальным, пригодным для обработки всего многообразия данных на объектах добычи, транспорта и хранения нефтепродуктов. Несмотря на универсальность метода, единство вычислительных процедур открывает широкие пути для глубокой унификации функциональных блоков ИИС при небольшой аппаратурной избыточности. Принято считать, что узкая специализация ограничивает область применения аппаратуры, уменьшает серийность ее выпуска, а более широкая универсальность приводит к излишней затрате электронных средств, к схемному усложнению и потере, как следствие, надежности. Как показали исследования и опыт построения локальных информационно-измерительных устройств со счетно-решающими блоками, реализующими метод цифровой кусочно-линейной аппроксимации, эта проблема в указанном смысле упрощается: оптимальная специализация может быть достигнута универсальными средствами при анализе и компоновке вычислительных задач в определенные группы.

Линейная аппроксимация анодной характеристики диода.

Метод кусочно-линейной аппроксимации характеристики заключается в разбиении сложной криволинейной зависимости на ряд участков с последующей заменой этих участков кривой отрезками прямой линии.

Аппроксимация кривой намагничивания.| Петля гистерезиса ( а и кривая размагничивания ( б.

Метод кусочно-линейной аппроксимации кривой намагничивания дает возможность свести нелинейные задачи к линейным.

Сущность метода кусочно-линейной аппроксимации состоит в замене нелинейной характеристики отрезками прямых, что позволяет довольно точно аппроксимировать любую заданную нелинейную характеристику.

Применение метода кусочно-линейной аппроксимации, по-видимому, может привести к лучшему качеству решения в случаях, когда разделяющая поверхность имеет сложный и заранее неизвестный вид.

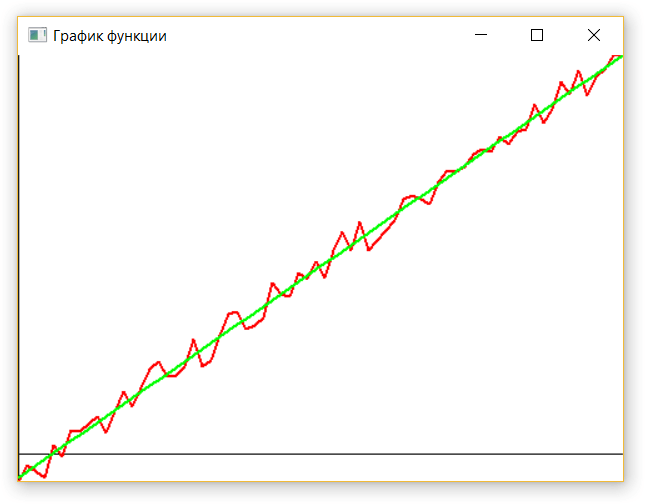
Построение графика функции

Обзор смартфона leeco le 2 (x527): заточенный под развлекательные функции

Для наглядности построим график функции, полученный аппроксимацией по методу наименьших квадратов. Подробнее о построении графика функции описано здесь. Реализация на Си

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149

#include <windows.h>const int NUM = 70; // количество точекLONG WINAPI WndProc(HWND, UINT, WPARAM, LPARAM);double **x; // массив данных // Определение коэффициентов линейной аппроксимации по МНКvoid getApprox(double **m, double *a, double *b, int n) { double sumx = 0; double sumy = 0; double sumx2 = 0; double sumxy = 0; for (int i = 0; i<n; i++) { sumx += m; sumy += m; sumx2 += m * m; sumxy += m * m; } *a = (n*sumxy — (sumx*sumy)) / (n*sumx2 — sumx*sumx); *b = (sumy — *a*sumx) / n; return;}// Задание исходных данных для графика// (двумерный массив, может содержать несколько рядов данных)double ** getData(int n) { double **f; double a, b; f = new double*; f = new double; f = new double; f = new double; for (int i = 0; i<n; i++) { double x = (double)i * 0.1; f = x; f = 8 * x — 3 + ((rand() % 100) — 50)*0.05; } getApprox(f, &a, &b, n); // аппроксимация for (int i = 0; i<n; i++) { double x = (double)i * 0.1; f = a*x + b; } return f;}// Функция рисования графикаvoid DrawGraph(HDC hdc, RECT rectClient, double **x, int n, int numrow = 1) { double OffsetY, OffsetX; double MAX_X = 0; double MAX_Y = 0; double ScaleX, ScaleY; double min, max; int height, width; int X, Y; // координаты в окне (в px) HPEN hpen; height = rectClient.bottom — rectClient.top; width = rectClient.right — rectClient.left; // Область допустимых значений X min = x; max = x; for (int i = 0; i<n; i++) { if (x < min) min = x; if (x > max) max = x; } double temp = max — min; MAX_X = max — min; OffsetX = min*width / MAX_X; // смещение X ScaleX = (double)width / MAX_X; // масштабный коэффициент X // Область допустимых значений Y min = x; max = x; for (int i = 0; i<n; i++) { for (int j = 1; j <= numrow; j++) { if (x < min) min = x; if (x > max) max = x; } } MAX_Y = max — min; OffsetY = max*height / (MAX_Y); // смещение Y ScaleY = (double)height / MAX_Y; // масштабный коэффициент Y // Отрисовка осей координат hpen = CreatePen(PS_SOLID, 0, 0); // черное перо 1px SelectObject(hdc, hpen); MoveToEx(hdc, 0, OffsetY, 0); // перемещение в точку (0;OffsetY) LineTo(hdc, width, OffsetY); // рисование горизонтальной оси MoveToEx(hdc, OffsetX, 0, 0); // перемещение в точку (OffsetX;0) LineTo(hdc, OffsetX, height); // рисование вертикальной оси DeleteObject(hpen); // удаление черного пера // Отрисовка графика функции int color = 0xFF; // красное перо для первого ряда данных for (int j = 1; j <= numrow; j++) { hpen = CreatePen(PS_SOLID, 2, color); // формирование пера 2px SelectObject(hdc, hpen); X = (int)(OffsetX + x * ScaleX); // координаты начальной точки графика Y = (int)(OffsetY — x * ScaleY); MoveToEx(hdc, X, Y, 0); // перемещение в начальную точку for (int i = 0; i<n; i++) { X = OffsetX + x * ScaleX; Y = OffsetY — x * ScaleY; LineTo(hdc, X, Y); } color = color << 8; // изменение цвета пера для следующего ряда DeleteObject(hpen); // удаление текущего пера }}// Главная функцияint WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow) { HWND hwnd; MSG msg; WNDCLASS w; x = getData(NUM); // задание исходных данных memset(&w, 0, sizeof(WNDCLASS)); w.style = CS_HREDRAW | CS_VREDRAW; w.lpfnWndProc = WndProc; w.hInstance = hInstance; w.hbrBackground = CreateSolidBrush(0x00FFFFFF); w.lpszClassName = «My Class»; RegisterClass(&w); hwnd = CreateWindow(«My Class», «График функции», WS_OVERLAPPEDWINDOW, 500, 300, 500, 380, NULL, NULL, hInstance, NULL); ShowWindow(hwnd, nCmdShow); UpdateWindow(hwnd); while (GetMessage(&msg, NULL, 0, 0)) { TranslateMessage(&msg); DispatchMessage(&msg); } return msg.wParam;}// Оконная функцияLONG WINAPI WndProc(HWND hwnd, UINT Message, WPARAM wparam, LPARAM lparam) { HDC hdc; PAINTSTRUCT ps; switch (Message) { case WM_PAINT: hdc = BeginPaint(hwnd, &ps); DrawGraph(hdc, ps.rcPaint, x, NUM, 2); // построение графика EndPaint(hwnd, &ps); break; case WM_DESTROY: PostQuitMessage(0); break; default: return DefWindowProc(hwnd, Message, wparam, lparam); } return 0;}

Примеры

Для приближённого вычисления интеграла используется формула прямоугольников или формула трапеций, или более сложная формула Симпсона. Фактически при этом происходит приближение подынтегральной функции ступенчатой функцией или вписанной ломаной, интеграл от которой считается мгновенно.
Для вычисления значений сложных функций часто используется вычисление значения отрезка ряда, аппроксимирующего функцию.

Обзор одной российской rtos, часть 8. работа с прерываниями

xy{\displaystyle x\qquad y}

20.3842{\displaystyle 2\quad 0.3842}

31.1062{\displaystyle 3\quad 1.1062}

42.6291{\displaystyle 4\quad 2.6291}

57.8320{\displaystyle 5\quad 7.8320}

617.379{\displaystyle 6\quad 17.379}

736.607{\displaystyle 7\quad 36.607}

866.696{\displaystyle 8\quad 66.696}

9104.43{\displaystyle 9\quad 104.43}

Если функция будет использована только для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:

y=ax5+bx4+cx3+dx2+fx+k{\displaystyle y=ax^{5}+bx^{4}+cx^{3}+dx^{2}+fx+k}

где:

a=−0.0190543{\displaystyle a=-0.0190543}

b=0.4874708{\displaystyle b=0.4874708}

c=−4.3207141{\displaystyle c=-4.3207141}

d=18.3040989{\displaystyle d=18.3040989}

f=−36.58884{\displaystyle f=-36.58884}

k=27.7555259{\displaystyle k=27.7555259}

Намного сложней обстоит дело в случае, если приведенные выше натурные данные служат опорными точками для выявления закона изменения y=F(x){\displaystyle y=F(x)} с известными граничными условиями. Например: F()={\displaystyle F(0)=0} и F(∞)→∞{\displaystyle F(\infty )\to \infty }. Тут уже качество результата зависит от профессионализма исследователя. В данном случае наиболее приемлемым окажется закон:

y=axbarctg(ecxd+f){\displaystyle y=ax^{b}\mathrm {arctg} {\big (}e^{cx^{d}+f}{\big )}}

где:

a=1.87926{\displaystyle a=1.87926}

b=1.76696{\displaystyle b=1.76696}

c=0.532588{\displaystyle c=0.532588}

d=1.01509{\displaystyle d=1.01509}

f=−4.16485{\displaystyle f=-4.16485}

Для оптимального подбора параметров уравнений обычно используют метод наименьших квадратов .

Аппроксимация с фиксированной точкой пересечения с осью y

В случае если в задаче заранее известна точка пересечения искомой прямой с осью y, в решении задачи останется только одна частная производная для вычисления коэффициента a.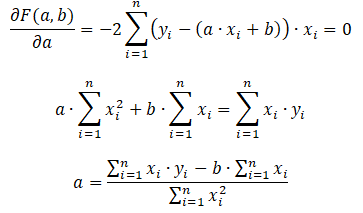
В этом случае текст программы для поиска коэффициента угла наклона аппроксимирующей прямой будет следующий (имя функции getApprox() заменено на getApproxA() во избежание путаницы).

12345678910111213141516171819202122232425262728293031323334353637383940414243444546

#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>// Задание начального набора значенийdouble ** getData(int n) { double **f; f = new double*; f = new double; f = new double; for (int i = 0; i<n; i++) { f = (double)i; f = 8 * (double)i — 3; // Добавление случайной составляющей //f = 8 * (double)i — 3 + ((rand() % 100) — 50)*0.05; } return f;}// Вычисление коэффициентов аппроксимирующей прямойvoid getApproxA(double **x, double *a, double b, int n) { double sumx = 0; double sumx2 = 0; double sumxy = 0; for (int i = 0; i<n; i++) { sumx += x; sumx2 += x * x; sumxy += x * x; } *a = (sumxy — b*sumx) / sumx2; return;}int main() { double **x, a, b; int n; system(«chcp 1251»); system(«cls»); printf(«Введите количество точек: «); scanf(«%d», &n); x = getData(n); for (int i = 0; i<n; i++) printf(«%5.1lf — %7.3lf\n», x, x); b = 0; getApproxA(x, &a, b, n); printf(«a = %lf\nb = %lf», a, b); getchar(); getchar(); return 0;}

b=0Алгоритмизация

Аппроксимация линейной функцией

Любая линейная функция может быть записана уравнением
Аппроксимация заключается в отыскании коэффициентов a и b уравнения таких, чтобы все экспериментальные точки лежали наиболее близко к аппроксимирующей прямой.
С этой целью чаще всего используется метод наименьших квадратов (МНК), суть которого заключается в следующем: сумма квадратов отклонений значения точки от аппроксимирующей точки принимает минимальное значение: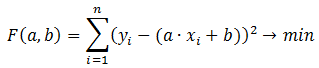
Решение поставленной задачи сводится к нахождению экстремума указанной функции двух переменных. С этой целью находим частные производные функции функции по коэффициентам a и b и приравниваем их к нулю.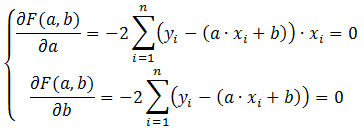
Решаем полученную систему уравнений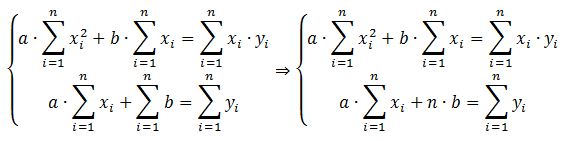
Определяем значения коэффициентов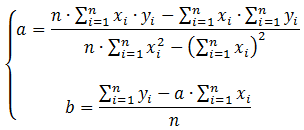
Для вычисления коэффициентов необходимо найти следующие составляющие: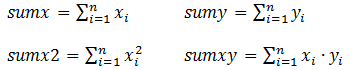
Тогда значения коэффициентов будут определены как