Колебательный контур принцип работы

Опыты Резерфорда

Верна ли модель Томсона? Как в действительности распределены положительные и отрицательные заряды внутри атома? Чтобы ответить на эти вопросы, нужен был эксперимент, позволяющий проникнуть внутрь атома. Ученик Томсона, знаменитый английский физик Эрнест Резерфорд предложил с этой целью бомбардировать атом высокоэнергетичными ?-частицами и смотреть, как они будут отклоняться положительным зарядом атома.
Что такое -частицы? Потоки этих частиц — так называемые «альфа-лучи» — были обнаружены при радиоактивном распаде некоторых элементов (например, радия). В результате тщательных исследований, проведённых опять-таки Резерфордом, было установлено, что каждая -частица имеет положительный заряд, равный по модулю удвоенному заряду электрона, и массу, превышающую массу электрона примерно в раз. То есть, -частица оказалась полностью ионизованным (лишённым электронов) атомом гелия.

Резерфорд говорил об -частицах как об ионах гелия; сейчас мы знаем, что это ядра гелия.

Но в те времена об атомных ядрах ещё ничего не знали — о них Резерфорду лишь предстояло догадаться, глядя на результаты своих знаменитых опытов!

Энергия -частиц очень велика — достаточно сказать, что скорость их вылета из радиоактивного образца составляет примерно скорости света. Поэтому интересно было выяснить, на какие углы будут отклоняться столь мощные «снаряды» при рассеянии на отдельных атомах, а точнее — на их положительных зарядах.

Пучок -частиц направлялся на тончайшую золотую фольгу. Как гласит история, Резерфорд не сомневался в том, что углы отклонения должны быть весьма малы: имея столь огромную энергию, -частицы должны проходить сквозь фольгу как нож сквозь масло. Только «для очистки совести», на всякий случай, он попросил учеников посмотреть, не возникает ли рассеяния -частиц на большие углы.

Каково же было всеобщее удивление, когда такие частицы обнаружились! Да, как и следовало ожидать, подавляющая доля -частиц отклонялась несущественно. Но совсем небольшая их часть (примерно одна частица из нескольких тысяч) отклонялась на угол, больший (рис. 2).

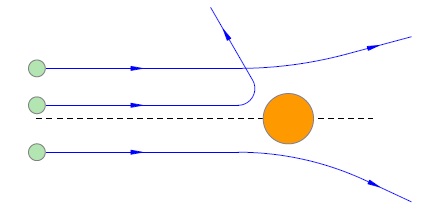
Рис. 2. Рассеяние -частиц на атомах

Эти отклонения казались совершенно невероятными. По словам Резерфорда, дело выглядело так, словно артиллерийский снаряд налетел на кусок бумаги и от удара повернул назад.

А «бумагой» в образном сравнении Резерфорда служил атом, устроенный согласно модели Томсона. Действительно, допустим, что положительный заряд атома «размазан» по всему атому, то есть шару радиусом см. Этот положительный заряд создаёт электрическое поле, тормозящее и отклоняющее -частицы. Вблизи атома потенциал данного поля:

Расчёты, однако, показывают, что такое поле оказывается слишком слабым — его тормозящего действия никак не хватит для того, чтобы остановить -частицу и отбросить её назад!

Таким образом, наличие -частиц, отброшенных фольгой, опровергло модель Томсона. Что же было предложено взамен?

Варианты конструкции контура

Кроме простых цепей «катушка-конденсатор» и «катушка-резистор-конденсатор», существуют и другие варианты, использующие в качестве основы колебательный контур. Это, например, параллельный контур, который отличается тем, что существует как элемент электрической цепи (потому как, существуй он отдельно, то являлся бы последовательной цепью, о которой и шла речь в статье).

Также существуют и другие виды конструкции, включающие разные электротехнические компоненты. Например, можно подключать в сеть транзистор, который будет размыкать и замыкать цепь с частотой, равной частотой колебаний в контуре. Таким образом, в системе установятся незатухающие колебания.

Добротность

Есть ещё одна важная величина, характеризующая работу контура, — добротность. Для того чтобы понять, что это такое, следует обратиться к такому процессу, как резонанс. Это явление, при котором амплитуда становится максимальной при неизменной величине силы, которая это колебание поддерживает. Объяснить резонанс можно на простом примере: если вы начнёте подталкивать качели в такт их частоте, то они будут ускоряться, а их «амплитуда» будет возрастать. А если будете толкать не в такт, то они будут замедляться. При резонансе очень часто рассеивается много энергии. Для того чтобы можно было вычислить величины потерь, придумали такой параметр, как добротность. Она представляет собой коэффициент, равный отношению энергии, находящейся в системе, к потерям, происходящим в цепи за один цикл.

Добротность контура вычисляется по формуле:

Q = (w0*W)/P, где w0 — резонансная циклическая частота колебаний; W — энергия, запасённая в колебательной системе; P — рассеиваемая мощность.

Этот параметр — безразмерная величина, так как фактически показывает отношение энергий: запасённой к потраченной.

Планетарная модель атома

Чтобы отбросить -частицу, положительный заряд атома должен создавать куда более сильное электрическое поле, чем то, которое получается в модели Томсона. А чтобы создать такое поле, положительный заряд должен быть сосредоточен в области, гораздо меньшей размера атома.

Размер этой области можно вычислить. Если положительный заряд занимает область размером , то вблизи заряда создаётся электрическое поле с потенциалом

Зная кинетическую энергию -частицы, можно найти величину тормозящего потенциала , а затем и размер положительно заряженной области. Вычисления, проведённые Резерфордом, дали следующий результат:

см.

Эта величина на пять порядков (в сто тысяч раз!) меньше размера атома. Так на смену модели Томсона пришла планетарная модель атома (рис. 3).

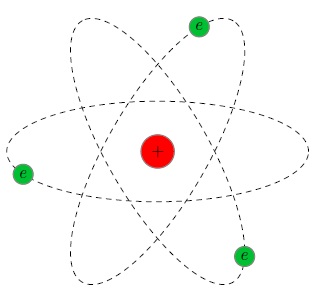
Рис. 3. Планетарная модель атома

В центре атома находится крошечное положительно заряженное ядро, вокруг которого, словно планеты вокруг Солнца, движутся электроны. Между ядром и электронами действуют силы кулоновского притяжения, но упасть на ядро электроны не могут за счёт своего движения — точно так же, как и планеты не падают на Солнце, хоть и притягиваются к нему.

Заряд ядра по модулю равен суммарному заряду электронов, так что атом в целом электрически нейтрален. Однако электроны могут быть выбиты из своих орбит и покинуть атом — тогда атом превращается в положительно заряженный ион.

Масса электронов составляет очень малую часть общей массы атома. Например, в атоме водорода всего один электрон, и его масса в раз меньше массы ядра. Следовательно, почти вся масса атома сосредоточена в ядре — и это при том, что ядро в сто тысяч раз меньше самого атома.

Чтобы лучше почувствовать соотношение масштабов атома и ядра, представьте себе, что атом стал размером с Останкинскую телебашню ( м). Тогда ядро окажется горошиной размером мм, лежащей у вас на ладони. И тем не менее, почти вся масса атома заключена в этой горошине!

Модель Томсона

Первую модель строения атома придумал английский физик Джозеф Джон Томсон (удостоенный Нобелевской премии за открытие электрона). В конечном счёте она оказалась неверной, но сыграла важную роль, будучи стимулом последующих экспериментальных исследований Резерфорда. Физики называли модель Томсона «пудинг с изюмом».

Согласно Томсону атом представляет собой шар размером порядка см. По этому шару некоторым образом распределён положительный заряд, а внутри шара, подобно изюминкам, находятся электроны (рис. 1).

Рис. 1. Модель атома Томсона

Суммарный заряд электронов в точности равен положительному заряду шара, поэтому атом в целом электрически нейтрален.

Излучение атомов объясняется колебаниями электронов около положений равновесия (как вы помните, любой ускоренно движущийся заряд излучает электромагнитные волны). Однако вся совокупность экспериментальных данных по атомным спектрам не укладывалась в модель Томсона. Например, для некоторых химических элементов были подобраны формулы, хорошо описывающие их спектры, но эти формулы из модели Томсона никак не следовали.

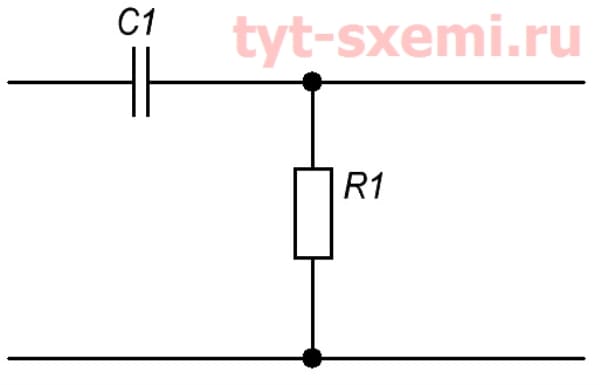
Последовательный колебательный контур

Если соединить последовательно электрический конденсатор и катушку индуктивности, то для синусоидального сигнала определенной частоты указанная схема будет демонстрировать нулевое реактивное сопротивление. Этот эффект называется резонансом колебательного контура, сама схема из конденсатора и индуктивности — последовательным колебательным контуром, а частота, на которой проявляется этот эффект — частотой резонанса.

Хотя и катушка индуктивности, и конденсатор имеют некоторое реактивное сопротивление, вместе они реактивного сопротивления не проявляют. Причина проста. Конденсатор и катушка накапливают и отдают энергию, но делают это по-разному. В тот момент, когда катушка накапливает энергию, конденсатор ее отдает, и наоборот. Конечно, этот эффект проявляется только для синусоидального сигнала, на определенной частоте, в установившемся режиме. Если частота сильно отличается от резонансной, то схема теряет свои чудесные качества и проявляет себя, как катушка и конденсатор. Если последовательный колебательный контур не был запитан, а теперь на него подали синусоидальный сигнал резонансной частоты, то сопротивление будет уменьшаться постепенно, по мере перехода контура в стационарный режим работы.

Если пропускать через последовательный колебательный контур синусоидальный электрический ток резонансной частоты, то падение напряжения на контуре будет равно нулю. Но падение напряжения на конденсаторе отдельно, индуктивности отдельно будет иметь место. Просто эти напряжения компенсируют друг друга в каждый момент времени. Напряжения на конденсаторе и катушке могут быть очень значительными. Одной из популярных ошибок при проектировании последовательного колебательного контура является неправильная оценка напряжения на конденсаторе. Напряжение может в разы, десятки, сотни раз превышать напряжение источника питания. На основе этого эффекта даже разработаны схемы повышающих преобразователей напряжения.

[Амплитудное значение напряжения на конденсаторе, В] = [Амплитудное значение силы тока через контур, А] * [ZC], где [ZC] = 1 / (2 * ПИ * [Частота сигнала, Гц] * [Емкость конденсатора, Ф])

Необходимо также обратить внимание, чтобы ток через последовательный контур не приводил к насыщению сердечника катушки индуктивности. В схемотехнике последовательный колебательный контур применяется, если необходимо пропустить сигнал определенной частоты и отфильтровать все другие

Колебательные контуры бывают небольшие, рассчитанные на работу с небольшими токами и напряжениями, например, во входных и внутренних цепях радиоприемника. Но бывают и силовые, рассчитанные на большие токи и напряжения, например, в радиопередатчиках, силовых резонансных фильтрах и т. д

В схемотехнике последовательный колебательный контур применяется, если необходимо пропустить сигнал определенной частоты и отфильтровать все другие. Колебательные контуры бывают небольшие, рассчитанные на работу с небольшими токами и напряжениями, например, во входных и внутренних цепях радиоприемника. Но бывают и силовые, рассчитанные на большие токи и напряжения, например, в радиопередатчиках, силовых резонансных фильтрах и т. д.

Что такое ёмкость конденсатора?

Ёмкость конденсатора представляет собой отношение заряда конденсатора к напряжению, под которым он находится. Посчитать эту величину можно очень просто с помощью математической формулы:

C = (e0*S)/d, гдеe0 — диэлектрическая проницаемость материала диэлектрика (табличная величина), S — площадь обкладок конденсатора, d — расстояние между пластинами.

Зависимость ёмкости конденсатора от расстояния между обкладками объясняется явлением электростатической индукции: чем меньше расстояние между пластинами, тем сильнее они влияют друг на друга (по закону Кулона), тем больше заряд обкладок и меньше напряжение. А при уменьшении напряжения увеличивается значение ёмкости, так как её также можно описать следующей формулой:

C = q/U, гдеq — заряд в кулонах.

Стоит поговорить о единицах измерения этой величины. Ёмкость измеряется в фарадах. 1 фарад — достаточно большая величина, поэтому существующие конденсаторы (но не ионисторы) имеют ёмкость, измеряемую в пикофарадах (одна триллионная фарада).

Методы определения добротности

Пользуясь
определением добротности, можно показать,
что

,
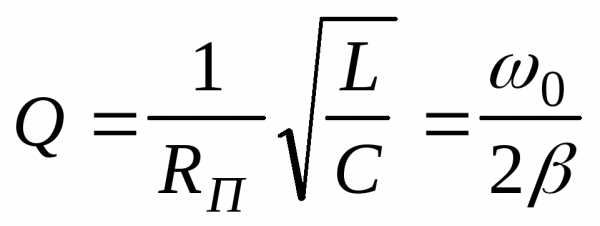(9)

R_П
= r + R + R_L,

где R_П
– полное сопротивление цепи; r
– внутреннее сопротивление источника
тока; R
– сопротивление, включенное в контур;
R_L
– активное сопротивление катушки
индуктивности.

1. Расчет
теоретического значения добротности.
Добротность контура Q_теор
можно рассчитать по формуле (9), зная
параметры электрической цепи R_П,
L
и C.

2. Определение
добротности по измерениям резонансного
напряжения U_рез
и амплитуды вынуждающей ЭДС .
Соотношение (8) при малых коэффициентах
затухания принимает вид

,

откуда

.
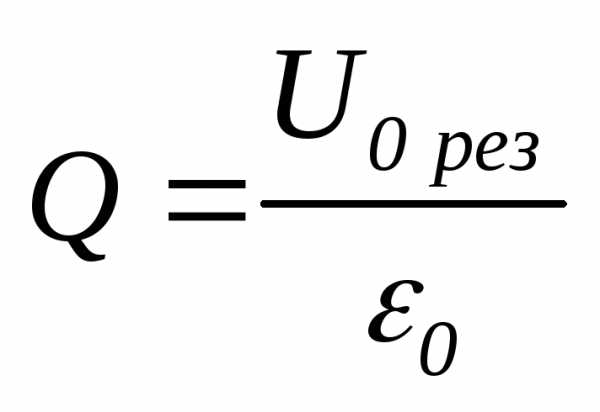(10)

3. Определение
добротности по ширине резонансной
кривой.
Шириной резонансной кривой называется
разность частот, при которых достигается
эффективное значение резонансного
напряжения на конденсаторе, равное (см.
рис. 3)
.

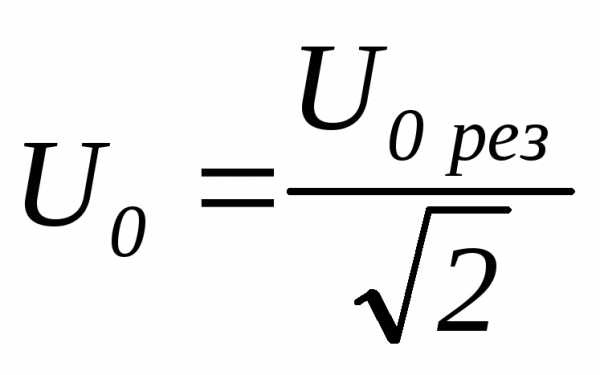Разность этих
частот 
= ₂
– ₁является
полосой пропускания контура.

Энергия, запасенная
в контуре при резонансе, на границах
полосы пропускания уменьшается в два
раза.

Пользуясь
соотношениями (9) и (10) и преобразуя
уравнение (5), получаем, что с достаточной
степенью точности

.
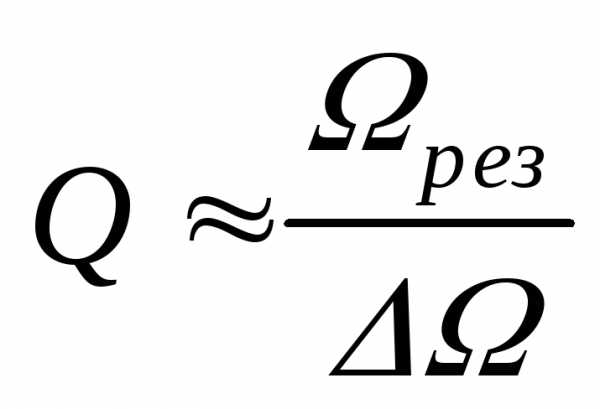(11)

Таким
образом, зная 
и _рез,
можно вычислить добротность контура.

Расчет добротности
этим методом производится с помощью
полученной экспериментально резонансной
кривой в координатах U, .
По ней определяются для
значения
₁
и ₂
слева и справа от _рез.

Вместо _рез
и циклических частот ₁
и ₂
используются соответствующие частоты
генератора

.
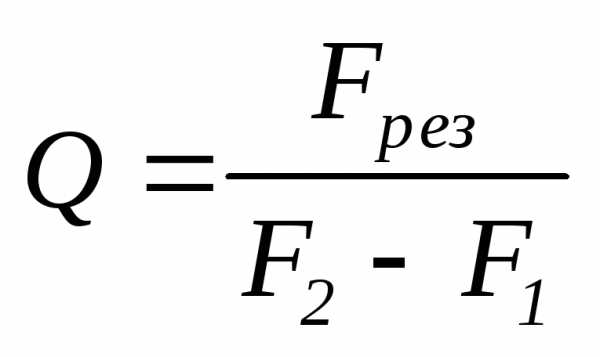(12)

Метод измерения и описание аппаратуры

Для выполнения
работы используется простейший
колебательный контур из последовательно
соединенных катушки индуктивности L,
конденсатора C
и сопротивления R.
Резонансные кривые снимают при различных
сопротивлениях, включенных в контур.
Наблюдение за изменением амплитуды
колебаний на конденсаторе производится
с помощью электронного осциллографа.
Для этого сигнал с конденсатора подается
на вход осциллографа, и при изменении
частоты генератора измеряется амплитуда
напряжения. При этом диапазон частот
выбирается достаточно широким в обе
стороны по отношению к резонансной
частоте. Резонансная частота соответствует
наибольшей амплитуде измеряемого
напряжения при заданном сопротивлении
контура. Определение добротности контура
производится двумя из вышеописанных
способов: по ширине резонансной кривой
и по отношению резонансного напряжения
к амплитуде вынуждающей ЭДС. Полученные
результаты позволяют вычислить омическое
сопротивление контура и оценить значение
внутреннего сопротивления генератора.

Порядок выполнения работы

1. Включите генератор
   синусоидальных колебаний и электронный
   осциллограф и соберите схему для
   измерений в соответствии с указаниями
   на стенде.

2. Рассчитайте
   собственную частоту контура по формуле

.

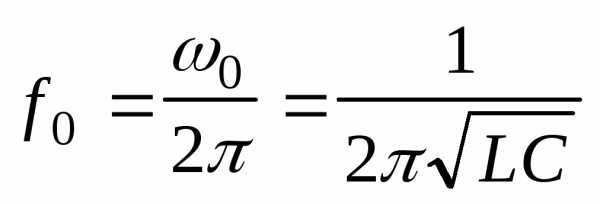Параметры L,
C,
R_L,
r контура
даны на стенде. Значения L,
Cи f
запишите в
табл. 1.

1. Определите по
   осциллографу амплитуды вынужденных
   колебаний напряжения U,
   сни­маемого с конденсатора в делениях
   масштабной сетки на экране осциллографа,
   при фиксированных значениях частоты
   F
   генератора в выбранном диапазоне частот
   при R₁.
   Полученные данные занесите в табл. 1.

2. Повторите опыт
   (пункт 3) при другом сопротивлении R₂,
   включенном в контур.

3. Не изменяя
   настройки генератора определите
   амплитуду колебаний ЭДС генератора,
   соответствующую резонансной частоте,
   полученной экспериментально в п. 3,4.
   Для этого установите на генераторе
   резонансную частоту, выход генератора
   подключите непосредственно к входу
   электронного осциллографа с помощью
   переключателя на стенде, и зафиксируйте
   амплитуду сигнала .
   Результат занесите в табл. 1 и табл. 2.

4. По данным табл.
   1 постройте резонансные кривые при
   различных сопротивлениях контура R₁
   и R₂.

5. На каждой
   резонансной кривой отметьте уровень,
   соответствующий 0,7U
   _рез.

Таблица 1

С
= … Ф; f
= … КГц;

L
= … Гн; 
= … В.

Вынужденные электромагнитные колебания. Резонанс

Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:

где ​\( \varepsilon \)​ – мгновенное значение ЭДС, \( \varepsilon_m \) – амплитудное значение ЭДС.

При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.

Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.

Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ​\( \varphi_L=-\pi/2 \)​, а на конденсаторе \( \varphi_C=\pi/2 \)​. Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:

Резонансная частота вычисляется по формуле:

Важно! Резонансная частота не зависит от активного сопротивления ​\( R \)​. Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс

Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ​\( (R\to0) \)​, то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.

График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.

Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.

При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.

Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.

Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.

Практическое применение

Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях, радиоприёмниках, а также в различных устройствах автоматики. Например, на самолётах Ил-62М, Ил-76 и установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от генератора (сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя.

Математическое описание процессов

Напряжение на идеальной катушке индуктивности при изменении протекающего тока:

uL=LdiLdt.{\displaystyle u_{L}=L{\frac {di_{L}}{dt}}.}

Ток, протекающий через идеальный конденсатор, при изменении напряжения на нём:

iC=CduCdt.{\displaystyle i_{C}=C{\frac {du_{C}}{dt}}.}

Из правил Кирхгофа, для цепи, составленной из параллельно соединённых конденсатора и катушки, следует:

uL+uC=,{\displaystyle u_{L}+u_{C}=0,} — для напряжений,

и

iC=iL{\displaystyle i_{C}=i_{L}} — для токов.

Совместно решая систему дифференциальных уравнений (дифференцируя одно из уравнений и подставляя результат в другое), получаем:

d2q(t)dt2+1LCq(t)={\displaystyle {\frac {d^{2}q(t)}{dt^{2}}}+{\frac {1}{LC}}q(t)=0.}

Это дифференциальное уравнение гармонического осциллятора с циклической частотой собственных колебаний ω=1LC{\displaystyle \omega ={\frac {1}{\sqrt {LC}}}} (она называется собственной частотой гармонического осциллятора).

Решением этого уравнения 2-го порядка является выражение, зависящее от двух начальных условий:

i(t)=Iasin⁡(ωt+φ),{\displaystyle i(t)=I_{a}\sin({\omega }t+\varphi ),}

где Ia{\displaystyle I_{a}} — некая постоянная, определяемая начальными условиями, называемая амплитудой колебаний, φ{\displaystyle \varphi } — также некоторая постоянная, зависящая от начальных условий, называемая начальной фазой.

Например, при начальных условиях φ={\displaystyle \varphi =0} и амплитуде начального тока Ia{\displaystyle I_{a}} решение сведётся к:

i(t)=Iasin⁡(ωt).{\displaystyle i(t)=I_{a}\sin({\omega }t).}

Решение может быть записано также в виде

i(t)=Ia1sin⁡(ωt)+Ia2cos⁡(ωt),{\displaystyle i(t)=I_{a1}\sin({\omega }t)+I_{a2}\cos({\omega }t),}

где Ia1{\displaystyle I_{a1}} и Ia2{\displaystyle I_{a2}} — некоторые константы, которые связаны с амплитудой Ia{\displaystyle I_{a}} и фазой φ{\displaystyle \varphi } следующими тригонометрическими соотношениями:

Ia1=Iacos⁡(φ),{\displaystyle I_{a1}=I_{a}\cos {(\varphi )},}

Ia2=Iasin⁡(φ).{\displaystyle I_{a2}=I_{a}\sin {(\varphi )}.}