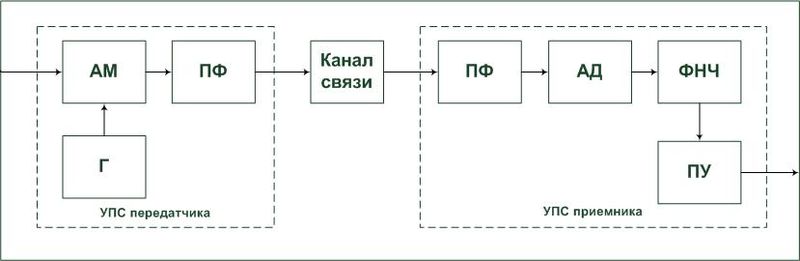
Последовательный lc контур расширяет диапазон перестройки гун

Как измерить добротность: формулы

В домашних условиях этот параметр динамиков часто рассчитывается с использованием простого милливольтметра переменного тока. Также для этой процедуры подготавливают плату и резистор 1000 Ом, стабилизирующий ток через динамик. Кроме того, при использовании такой методики понадобится программный генератор от компьютера и усилитель мощности (для подачи сигнала на динамик). Производят процедуру измерения добротности с применением такого оборудования следующим образом:

• динамик подвешивают в свободном состоянии, к примеру, на какой-нибудь веревке;

• собирают схему.

Перед сборкой схемы строят график, где по оси y откладывают напряжение в милливольтах (100, 200, 300). На х при этом указывают частоту (10, 20, 30…140 и т. д). Далее собирают схему, где сигнал с усилителя подается на резистор, а затем идет на динамик.

На следующем этапе:

• включают милливольтметр в схему в точках а и с и устанавливают напряжение 10-20 В на частоте 500-1000 герц;

• подключают вольтметр к точкам в и с, путем регулировки генератора находят частоту, где значения вольтах максимальны (Fs);

• изменяют частоту вверх по отношению к Fs и находят точки, в которых показания вольтметра значительно меньше Fs и постоянны (Um).

Измеряя напряжение при определенной частоте динамика, строят соответствующий график. На следующем этапе находят среднее значение между минимальным напряжением и максимальным. При этом используют формулу U1/2=√Umax*Umin. Полученное значение в виде горизонтальной линии переносят на график и находят точки пересечения с линиями отношения F1 и F2 (с соответствующими показателями частоты).

Далее находят акустическую добротность по формуле Qa=√Umax/Umin * Fs/F2-F1, где Fs — значение частоты при максимальных показаниях милливольтметра. Затем можно найти электрическую добротность:

Qes=Qa*Umin/(Umax-Umin).

После этого вычисляют полную добротность динамика:

Qts=Qa*Qes/(Qa+Qes).

На следующем этапе строят график для второго динамика и производят такие же вычисления.

Способы измерения дополнительных параметров

Как уже упоминалось, помимо трех основных характеристик ТС, при конструировании акустических систем могут использоваться и другие показатели. К примеру, сопротивление обмотки головки постоянному току Re измеряют на частоте, близкой к 0 Гц или же просто с использованием омметра.

Площадь диффузора Sd или, как еще ее называют эффективная излучающая поверхность, в низких частотах совпадает с конструктивной. Находят этот параметр с использованием простой формулы Sd=nR2. При этом за радиус принимают половину расстояния от середины резинового подвеса по ширине с одной стороны до середины противоположной. Связано это прежде всего с тем, что половина ширины подвеса также является излучающей поверхностью.

Комплексное сопротивление (импеданс) колебательного контура

Колебательный контур может быть рассмотрен как двухполюсник, представляющий собой параллельное включение конденсатора и катушки индуктивности. Комплексное сопротивление такого двухполюсника можно записать как

z^(iω)=iωL1−ω2LC,{\displaystyle {\hat {z}}(i\omega )\;={\frac {i\omega L}{1-\omega ^{2}LC}},}

где i — мнимая единица.

Для такого двухполюсника может быть определена т. н. характеристическая частота (или резонансная частота), когда импеданс колебательного контура стремится к бесконечности (знаменатель дроби стремится к нулю).

Эта частота равна

ωh=1LC{\displaystyle \omega _{h}={\frac {1}{\sqrt {LC}}}}

и совпадает по значению с собственной частотой колебательного контура.

Из этого уравнения следует, что на одной и той же частоте может работать множество контуров с разными величинами L и C, но с одинаковым произведением LC. Однако выбор соотношения между L и C зачастую не бывает полностью произвольным, так как обуславливается требуемым значением добротности контура.

Для последовательного контура добротность растёт с увеличением L:

Q=1RLC,{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}},}

где R — активное сопротивление контура.
Для параллельного контура:

Q=ReCL,{\displaystyle Q=R_{e}{\sqrt {\frac {C}{L}}},}

где Re=LCRL+C{\displaystyle R_{e}={\frac {L}{CR_{L+C}}}}, (RL+C{\displaystyle R_{L+C}} — сумма активных сопротивлений в цепи катушки и цепи конденсатора).

Понятие добротности связано с тем, что в реальном контуре существуют потери энергии (на излучение и нагрев проводников). Обычно считают, что все потери сосредоточены в некотором эквивалентном сопротивлении Re{\displaystyle R_{e}}, которое в последовательном контуре включено последовательно с L и C, а в параллельном — параллельно им. Малые потери (то есть высокая добротность) означают, что Re{\displaystyle R_{e}} в последовательном контуре мало, а в параллельном — велико. В низкочастотном последовательном контуре Re{\displaystyle R_{e}} легко обретает физический смысл — это активное сопротивление провода катушки и проводников цепи.

Из чего он состоит?

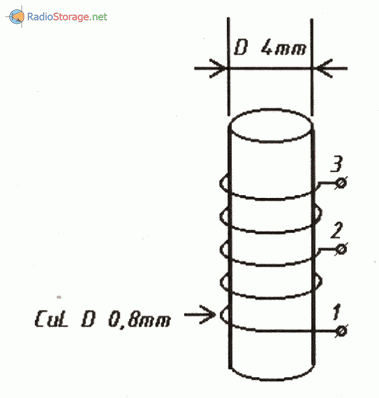
Колебательный контур состоит из катушки и конденсатора. Кроме того, в нём также может присутствовать резистор (элемент с переменным сопротивлением). Катушка индуктивности (или соленоид, как её иногда называют) представляет собой стержень, на который наматываются несколько слоёв обмотки, которая, как правило, представляет собой медную проволоку. Именно этот элемент создаёт колебания в колебательном контуре. Стержень, находящийся в середине, часто называют дросселем, или сердечником, а катушку иногда именуют соленоидом.

Катушка колебательного контура создаёт колебания только при наличии запасённого заряда. При прохождении через неё тока она накапливает заряд, который затем отдаёт в цепь, если напряжение падает.

Провода катушки обычно имеют очень маленькое сопротивление, которое всегда остаётся постоянным. В цепи колебательного контура очень часто происходит изменение напряжения и силы тока. Это изменение подчиняется определённым математическим законам:

U = U0*cos(w*(t-t0) , где U — напряжение в данный момент времени t, U0 — напряжение во время t0, w — частота электромагнитных колебаний.

Другим неотъемлемым компонентом контура является электрический конденсатор. Это элемент, состоящий из двух обкладок, которые разделены между собой диэлектриком. При этом толщина слоя между обкладками меньше их размеров. Такая конструкция позволяет накапливать на диэлектрике электрический заряд, который потом можно отдать в цепь.

Отличие конденсатора от аккумулятора в том, что в нём не происходит превращения веществ под действием электрического тока, а происходит непосредственное накопление заряда в электрическом поле. Таким образом, с помощью конденсатора можно накопить достаточно большой заряд, отдавать который можно весь сразу. При этом сила тока в цепи сильно возрастает.

Также колебательный контур состоит из ещё одного элемента: резистора. Этот элемент обладает сопротивлением и предназначен для контролирования силы тока и напряжения в цепи. Если при постоянном напряжении увеличивать сопротивление резистора, то сила тока будет уменьшаться по закону Ома:

I = U/R , где I — сила тока, U — напряжение, R — сопротивление.

Теория и практика

На что влияет добротность динамика, таким образом, понятно. Как мы выяснили, при использовании акустического оформления этот показатель должен быть достаточно низким. Именно таким образом дело обстоит в теории. Однако на практике низкодобротные динамики встречаются, к сожалению, довольно-таки редко. Даже, к примеру, при использовании фазоинвертора, требующего, как мы выяснили, показателя в 0,5-0,6, часто применяются головки с показателем выше единицы.

У любого звукоизлучающего устройства имеется своя собственная резонансная частота. И именно через нее мембраны после резких сигналов приходят в равновесное состояние. Во многих случаях при высокой добротности динамик будет даже не продлевать или доигрывать какие-либо ноты. При прекращении внешнего воздействия он просто-напросто начнет неприятно гудеть. Именно таким образом ведут себя на определенной частоте, к примеру, дешевые компьютерные колонки.

При всем при этом дорогие динамики с большой добротностью выдают чаще всего достаточно качественный звук. Дело здесь заключается прежде всего в том, что такие устройства обычно имеют еще и довольно-таки низкую резонансную частоту. При таком условии шумы воспринимаются не особенно хорошо натренированным в плане акустики человеческим ухом не как досадные «помехи», а просто, как очень мощный звук. В особенности незаметной подобная «грязь» становится при прослушивании простой музыки, к примеру, современной попсы. То есть гул в данном случае проходит по «правильной» частоте.

Последовательное соединение

При последовательном соединении, согласно Закону Ома для переменного тока,
во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора U_R = IR; на выводах конденсатора U_C = IX_C; на выводах катушки U_L = IX_L.

Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах U_X = U_L — U_C .
Пропорционально напряжению, получим общее реактивное сопротивление X = X_L — X_C .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.U , U_R и U_X представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.

Тогда получим соотношение, согласно Теореме Пифагора, U ² = U_R² + U_X² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах,
определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.

X_L = ωL = 2πfL — реактивное сопротивление индуктивности.X_C = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.

Угол сдвига фаз φ и его дополнение до 90° δ
определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:

Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа,
где действительной его частью является активное сопротивление, а мнимой — реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:

Z = R + jX

Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:

Z = |Z|ejargZ = Zejφ

Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.

Теория

Q=ωWPd=2πfWPd{\displaystyle Q={\frac {\omega _{0}W}{P_{d}}}={\frac {2\pi f_{0}W}{P_{d}}}},

где

• ω{\displaystyle \omega _{0}} — резонансная круговая частота колебаний
• f{\displaystyle f_{0}} — резонансная частота колебаний
• W{\displaystyle W} — энергия, запасённая в колебательной системе
• Pd{\displaystyle P_{d}} — рассеиваемая мощность.

Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.

Для последовательного колебательного контура в RLC-цепях, в котором все три элемента включены последовательно:

Q=1RLC=ωLR,{\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}}={\frac {\omega _{0}L}{R}},}

где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно, а ω{\displaystyle \omega _{0}} — частота резонанса. Выражение LC{\displaystyle {\sqrt {L/C}}} часто называют характеристическим или волновым сопротивлением колебательного контура. Таким образом, добротность в колебательном контуре равна отношению волнового сопротивления к активному.

Для параллельного контура, в котором индуктивность, ёмкость и сопротивление включены параллельно:

Q=RCL=RωL{\displaystyle Q=R{\sqrt {\frac {C}{L}}}={\frac {R}{\omega _{0}L}}}

Формулировка частотного отклика или ширины полосы пропускания колебательной системы

ЛАФЧХ колебательных звеньев с разной добротностью

В данном случае R является входным сопротивлением параллельного контура. Однако практически для электрической цепи гораздо проще измерить ток или напряжение, чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды колебаний, ширина полосы частот на АЧХ определяется на высоте 12{\displaystyle 1/{\sqrt {2}}} от высоты максимума (примерно −3 дБ). Поэтому чаще используется другое эквивалентное определение добротности, которое связывает ширину амплитудной резонансной кривой Δω{\displaystyle \Delta \omega } по уровню 12{\displaystyle 1/{\sqrt {2}}} с круговой частотой резонанса ω=2πf{\displaystyle \omega _{0}=2\pi f_{0}:}

Q=ωΔω=πδ=πNe,{\displaystyle Q={\frac {\omega _{0}}{\Delta \omega }}={\frac {\pi }{\delta }}=\pi N_{e},}

где δ — логарифмический декремент затухания, равный отношению полуширины резонансной кривой к частоте резонанса, Ne{\displaystyle N_{e}} — число колебаний за время релаксации.

Для электрически малых антенн добротность можно определить соотношением:

Q=ωWe+WmP{\displaystyle Q={\frac {\omega _{0}}{P}}},

где

• ω{\displaystyle \omega _{0}} — резонансная круговая частота электромагнитных колебаний
• We{\displaystyle W_{e}} — энергия электрического поля, запасённая в антенне
• Wm{\displaystyle W_{m}} — энергия магнитного поля, запасённая в антенне
• P{\displaystyle P} — рассеиваемая антенной мощность.

[Q] Как расчитать закрытый ящик?

Оформление «закрытый ящик» бывает двух типов, бесконечный экран и компрессионный подвес. Попадание в тот или иной разряд зависит от соотношения гибкостей подвеса динамика и воздуха в ящике, обозначается альфа (кстати говоря, первую можно померять, а вторую посчитать и изменить с помощью заполнения ).

Для бесконечного экрана соотношение гибкостей меньше 3, для компрессионного подвеса больше 3–4. Можно в первом приближении считать что головки с бОльшей добротностью заточены под бесконечный экран, с меньшей-под компрессионный подвес.

Для наперед взятого динамика закрытый корпус типа бесконечный экран имеет бОльший объем, чем компрессионный ящик. (Вообще говоря, когда есть динамик, то оптимальный корпус под него имеет однозначно определенный объем . Ошибки, возникшие при измерении параметров и расчетах, можно в небольших пределах поправить с помощью заполнения).

Динамики для закрытых корпусов имеют мощные магниты и мягкие подвесы в отличие от головок для открытых ящиков. Формула для резонансной частоты динамика в оформлении объемом V

F_с=F_s*SQRT(1+V_as/V)

,а приближенная формула, связывающая резонансные частоты и добротности головки в корпусе (индекс «с») и в открытом пространстве (индекс «s») F_c/Q_tc=F_s/Q_ts

Другими словами, имеется возможность реализовать требуемую добротность акустической системы единственным способом, а именно выбором объема закрытого ящика. Какую добротность выбрать? Люди, которые не слышали звучания натуральных музыкальных инструментов, обычно выбирают колонки с добротностью более1,0.

У колонок с такой добротностью (=1.0) наименьшая неравномерность частотной характеристики в области низших частот( а при чем здесь звук?), достигнутая ценой небольшого выброса на переходной характеристике. Максимально гладкая АЧХ получается при Q=0.7, а полностью апериодичная импульсная характеристика при Q=0.5. Hомограммы для расчетов можно взять в вышеприведенной книге.

Более подробнее и калькулятор можно найти в статье «Расчет закрытого ящика».

Практическое применение

Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях, радиоприёмниках, а также в различных устройствах автоматики. Например, на самолётах Ил-62М, Ил-76 и установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от генератора (сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя.

Активное сопротивление — колебательный контур

Активное сопротивление колебательного контура г равно сумме сопротивлений TL катушки и те конденсатора. Сопротивление г зависит от частоты. Это объясняется главным образом явлением поверхностного эффекта.
 

Если, активное сопротивление R колебательного контура равно нулю, то общая величина энергии контура остается неизменной, и свободные электромагнитные колебания называются незатухающими.
 

В большинстве случаев активное сопротивление колебательного контура определяется, главным образом, активным сопротивлением включенной в контур катушки индуктивности. С увеличением частоты индуктивное сопротивление катушки растет, но вследствие поверхностного эффекта растет и ее активное сопротивление.
 

В большинстве случаев активное сопротивление колебательного контура определяется главным образом актизным сопротивлением входящей в контур катушки. С увеличением частоты индуктивное сопротивление катушки растет, но вследствие поверхностного эффекта ( см.) растет и ее активное сопротивление.
 

В большинстве случаев активное сопротивление колебательного контура определяется главным образом активным сопротивлением входящей в контур катушки. С увеличением частоты индуктивное сопротивление катушки растет, но вследствие поверхностного эффекта ( см.) растет и ее активное сопротивление.
 

Множитель при I2 представляет собой активное сопротивление колебательного контура, характеризующее его способность к излучению. Его называют сопротивлением излучения.
 

Множитель при / 2 представляет собой активное сопротивление колебательного контура, характеризующего его способность к излучению. Его называют сопротивлением излучения.
 

Множитель при / 2 представляет собой активное сопротивление колебательного контура, характеризующее его способность к излучению. Его называют сопротивлением, излучения.
 

Множитель при / а представляет собою активное сопротивление колебательного контура, характеризующее его способность излучать энергию. Его называют сопротивлением излучения.
 

Множитель при / 2 представляет собой активное сопротивление колебательного контура, характеризующее его способность к излучению. Его называют сопротивлением излучения.
 

Этот метод служит для определения активного сопротивления колебательного контура. Другим вариантом является следующий. Нек-рый колебательный контур настраивают в резонанс с частотой лампового генератора.
 

Резонансным методом можно также измерять величину активного сопротивления колебательного контура, однако эти измерения значительно сложнее, и рассмотрение их выходит за рамки данной книги. Измерение добротности также обычно производят резонансным методом.
 

Определяют логарифмические декременты для различных емкостей и активных сопротивлений колебательного контура. Строят графики зависимости логарифмического декремента от емкости и сопротивления контура.