Text to binary converter
Содержание:
- Binary System
- Binary System
- Hexadecimal System (Hex System)
- What’s a decimal?
- Binary System
- What’s hexadecimal?
- Binary to ASCII text conversion table
- Hexadecimal to Decimal Table
- Binary System
- Преобразование шестнадцатеричного числа в десятичное
- Небольшое отступление
- What is a hex number?
- Таблица соответствия шестнадцатеричных цифр
- Хакерский редактор Hacker Viewer (Hiew) .
- Converting to and from hex numerals
- Decimal System
- Три системы счисления.
Binary System
The binary numeral system uses the number 2 as its base (radix). As a base-2 numeral system, it consists of only two numbers: 0 and 1.
While it has been applied in ancient Egypt, China and India for different purposes, the binary system has become the language of electronics and computers in the modern world. This is the most efficient system to detect an electric signal’s off (0) and on (1) state. It is also the basis for binary code that is used to compose data in computer-based machines. Even the digital text that you are reading right now consists of binary numbers.
Reading a binary number is easier than it looks: This is a positional system; therefore, every digit in a binary number is raised to the powers of 2, starting from the rightmost with 2. In the binary system, each binary digit refers to 1 bit.
Binary System
The binary numeral system uses the number 2 as its base (radix). As a base-2 numeral system, it consists of only two numbers: 0 and 1.
While it has been applied in ancient Egypt, China and India for different purposes, the binary system has become the language of electronics and computers in the modern world. This is the most efficient system to detect an electric signal’s off (0) and on (1) state. It is also the basis for binary code that is used to compose data in computer-based machines. Even the digital text that you are reading right now consists of binary numbers.
Reading a binary number is easier than it looks: This is a positional system; therefore, every digit in a binary number is raised to the powers of 2, starting from the rightmost with 2. In the binary system, each binary digit refers to 1 bit.
Hexadecimal System (Hex System)
The hexadecimal system (shortly hex), uses the number 16 as its base (radix). As a base-16 numeral system, it uses 16 symbols. These are the 10 decimal digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and the first six letters of the English alphabet (A, B, C, D, E, F). The letters are used because of the need to represent the values 10, 11, 12, 13, 14 and 15 each in one single symbol.
Hex is used in mathematics and information technologies as a more friendly way to represent binary numbers. Each hex digit represents four binary digits; therefore, hex is a language to write binary in an abbreviated form.
Four binary digits (also called nibbles) make up half a byte. This means one byte can carry binary values from 0000 0000 to 1111 1111. In hex, these can be represented in a friendlier fashion, ranging from 00 to FF.
In html programming, colors can be represented by a 6-digit hexadecimal number: FFFFFF represents white whereas 000000 represents black.
What’s a decimal?
A decimal or dec bit represents a single number, digit, or letter. A decimal is also called base 10 and denary as it consists of ten numbers. They are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
A decimal is a number system and can be represented using a subscription of 10 (i.e. 23510 reads as two hundred and thirty-five base 10).
Decimals are the numbers that we use in everyday counting. We use the decimal number system mostly because we have ten fingers. The number 10 is made using a combination of two of these decimal numbers: 1 and 0 while a number like 209 is a combination of three decimal numbers: 2, 0, and 9.
There is no limit as to how many times the numbers can be reused, that’s why it is often said that numbers never end.
Binary System
The binary numeral system uses the number 2 as its base (radix). As a base-2 numeral system, it consists of only two numbers: 0 and 1.
While it has been applied in ancient Egypt, China and India for different purposes, the binary system has become the language of electronics and computers in the modern world. This is the most efficient system to detect an electric signal’s off (0) and on (1) state. It is also the basis for binary code that is used to compose data in computer-based machines. Even the digital text that you are reading right now consists of binary numbers.
Reading a binary number is easier than it looks: This is a positional system; therefore, every digit in a binary number is raised to the powers of 2, starting from the rightmost with 2. In the binary system, each binary digit refers to 1 bit.
What’s hexadecimal?
Hexadecimal, also called base 16 or «hex» for short, is a representation of four binary bits and consists of seventeen numbers and letters. The hex numbers are the same as the decimal numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
The big difference between a hex and a decimal is that a hex contains letters as well. These are A, B, C, D, E, and F.
Using a subscript of 16 (i.e. 23516), a hex number can be represented. These letters come in ascending order after the decimals. Therefore, the hexadecimal series looks like this: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. A hex can be considered a shorter decimal version. For example, a large number in decimal shape has a much smaller hex equivalent (to represent the decimal number, hexadecimal uses less hex bits).
Binary to ASCII text conversion table
| Hexadecimal | Binary | ASCIICharacter |
|---|---|---|
| 00 | 00000000 | NUL |
| 01 | 00000001 | SOH |
| 02 | 00000010 | STX |
| 03 | 00000011 | ETX |
| 04 | 00000100 | EOT |
| 05 | 00000101 | ENQ |
| 06 | 00000110 | ACK |
| 07 | 00000111 | BEL |
| 08 | 00001000 | BS |
| 09 | 00001001 | HT |
| 0A | 00001010 | LF |
| 0B | 00001011 | VT |
| 0C | 00001100 | FF |
| 0D | 00001101 | CR |
| 0E | 00001110 | SO |
| 0F | 00001111 | SI |
| 10 | 00010000 | DLE |
| 11 | 00010001 | DC1 |
| 12 | 00010010 | DC2 |
| 13 | 00010011 | DC3 |
| 14 | 00010100 | DC4 |
| 15 | 00010101 | NAK |
| 16 | 00010110 | SYN |
| 17 | 00010111 | ETB |
| 18 | 00011000 | CAN |
| 19 | 00011001 | EM |
| 1A | 00011010 | SUB |
| 1B | 00011011 | ESC |
| 1C | 00011100 | FS |
| 1D | 00011101 | GS |
| 1E | 00011110 | RS |
| 1F | 00011111 | US |
| 20 | 00100000 | Space |
| 21 | 00100001 | ! |
| 22 | 00100010 | « |
| 23 | 00100011 | # |
| 24 | 00100100 | $ |
| 25 | 00100101 | % |
| 26 | 00100110 | & |
| 27 | 00100111 | ‘ |
| 28 | 00101000 | ( |
| 29 | 00101001 | ) |
| 2A | 00101010 | * |
| 2B | 00101011 | + |
| 2C | 00101100 | , |
| 2D | 00101101 | — |
| 2E | 00101110 | . |
| 2F | 00101111 | |
| 30 | 00110000 | |
| 31 | 00110001 | 1 |
| 32 | 00110010 | 2 |
| 33 | 00110011 | 3 |
| 34 | 00110100 | 4 |
| 35 | 00110101 | 5 |
| 36 | 00110110 | 6 |
| 37 | 00110111 | 7 |
| 38 | 00111000 | 8 |
| 39 | 00111001 | 9 |
| 3A | 00111010 | |
| 3B | 00111011 | ; |
| 3C | 00111100 | < |
| 3D | 00111101 | = |
| 3E | 00111110 | > |
| 3F | 00111111 | ? |
| 40 | 01000000 | @ |
| 41 | 01000001 | A |
| 42 | 01000010 | B |
| 43 | 01000011 | C |
| 44 | 01000100 | D |
| 45 | 01000101 | E |
| 46 | 01000110 | F |
| 47 | 01000111 | G |
| 48 | 01001000 | H |
| 49 | 01001001 | I |
| 4A | 01001010 | J |
| 4B | 01001011 | K |
| 4C | 01001100 | L |
| 4D | 01001101 | M |
| 4E | 01001110 | N |
| 4F | 01001111 | O |
| 50 | 01010000 | P |
| 51 | 01010001 | Q |
| 52 | 01010010 | R |
| 53 | 01010011 | S |
| 54 | 01010100 | T |
| 55 | 01010101 | U |
| 56 | 01010110 | V |
| 57 | 01010111 | W |
| 58 | 01011000 | X |
| 59 | 01011001 | Y |
| 5A | 01011010 | Z |
| 5B | 01011011 | |
| 5C | 01011100 | \ |
| 5D | 01011101 | |
| 5E | 01011110 | ^ |
| 5F | 01011111 | _ |
| 60 | 01100000 | ` |
| 61 | 01100001 | a |
| 62 | 01100010 | b |
| 63 | 01100011 | c |
| 64 | 01100100 | d |
| 65 | 01100101 | e |
| 66 | 01100110 | f |
| 67 | 01100111 | g |
| 68 | 01101000 | h |
| 69 | 01101001 | i |
| 6A | 01101010 | j |
| 6B | 01101011 | k |
| 6C | 01101100 | l |
| 6D | 01101101 | m |
| 6E | 01101110 | n |
| 6F | 01101111 | o |
| 70 | 01110000 | p |
| 71 | 01110001 | q |
| 72 | 01110010 | r |
| 73 | 01110011 | s |
| 74 | 01110100 | t |
| 75 | 01110101 | u |
| 76 | 01110110 | v |
| 77 | 01110111 | w |
| 78 | 01111000 | x |
| 79 | 01111001 | y |
| 7A | 01111010 | z |
| 7B | 01111011 | { |
| 7C | 01111100 | | |
| 7D | 01111101 | } |
| 7E | 01111110 | ~ |
| 7F | 01111111 | DEL |
Hexadecimal to Decimal Table
| Decimal
base 10 |
Hex
base 16 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
| 16 | 10 |
| 17 | 11 |
| 18 | 12 |
| 19 | 13 |
| 20 | 14 |
| 21 | 15 |
| 22 | 16 |
| 23 | 17 |
| 24 | 18 |
| 25 | 19 |
| 26 | 1A |
| 27 | 1B |
| 28 | 1C |
| 29 | 1D |
| 30 | 1E |
| 40 | 28 |
| 50 | 32 |
| 60 | 3C |
| 70 | 46 |
| 80 | 50 |
| 90 | 5A |
| 100 | 64 |
| 200 | C8 |
| 1000 | 3E8 |
| 2000 | 7D0 |
How to convert decimal to hexadecimal? Can you manually convert from decimal to hex?
To convert from decimal to hexadecimal, repeatedly divide the decimal number by 16. Then write the last remaining column you got in the hex equivalent column. If the rest is more than nine, remember to change it to its equivalent hex letter. The answer is taken from the last remainder obtained. See the diagram below as an example in order to convert to hexadecimal:
Example
|
Divisor |
Base Ten Number |
Remainder |
Hex Equivalent |
|---|---|---|---|
|
16 |
201 |
X |
X |
|
16 |
12 |
9 |
9 |
|
X |
12 |
C |
So the answer is C9. As you can see, it contains less bits than its 201 decimal equivalent.
Let’s understand how:
- Our decimal number (base 10) was divided by 16 to convert it to a hex equivalent (base 16).
- Our number of decimals was 201. We divided this by 16 to get a value of 12 with a remaining 9. The hex equivalent for 9 is 9, so no change has been made.
- Then we divided our previous answer, 12, by 16. We got a zero value and a 12 remaining value. Then we converted 12 to hex. The equivalent hex of 12 is C. Then, in the order from left to right, we wrote our answer from the last remaining we received to the first.
Decimal to hexadecimal converter
Prepostseo has developed dec to hex converter in order to convert decimal to hex easily and effortlessly. This tool generally called int to hex is also known as base 10 to base 16 converter. Moreover, you can convert hex to decimal using our online hex to dec converter. Apart this tool, we offer text to binary, decimal to binary, binary to decimal, and binary translator for free conversion.
We know it’s tough to convert to hex manually however our number to hex tool is a best option to do so without learning hard and fast rules of conversion. You can convert any decimal digit like 15 in hex or 100 in hex without any difficulty. You can put little effort in converting decimal to hexadecimal and rest of the hexadecimal conversion will be done by our string to hex converter. Give it a try once, folks!
Binary System
The binary numeral system uses the number 2 as its base (radix). As a base-2 numeral system, it consists of only two numbers: 0 and 1.
While it has been applied in ancient Egypt, China and India for different purposes, the binary system has become the language of electronics and computers in the modern world. This is the most efficient system to detect an electric signal’s off (0) and on (1) state. It is also the basis for binary code that is used to compose data in computer-based machines. Even the digital text that you are reading right now consists of binary numbers.
Reading a binary number is easier than it looks: This is a positional system; therefore, every digit in a binary number is raised to the powers of 2, starting from the rightmost with 2. In the binary system, each binary digit refers to 1 bit.
Decimal to Binary Conversion Chart Table
| Decimal | Binary |
|---|---|
| 1 | 00000001 |
| 2 | 00000010 |
| 3 | 00000011 |
| 4 | 00000100 |
| 5 | 00000101 |
| 6 | 00000110 |
| 7 | 00000111 |
| 8 | 00001000 |
| 9 | 00001001 |
| 10 | 00001010 |
| 11 | 00001011 |
| 12 | 00001100 |
| 13 | 00001101 |
| 14 | 00001110 |
| 15 | 00001111 |
| 16 | 00010000 |
| 17 | 00010001 |
| 18 | 00010010 |
| 19 | 00010011 |
| 20 | 00010100 |
| 21 | 00010101 |
| 22 | 00010110 |
| 23 | 00010111 |
| 24 | 00011000 |
| 25 | 00011001 |
| 26 | 00011010 |
| 27 | 00011011 |
| 28 | 00011100 |
| 29 | 00011101 |
| 30 | 00011110 |
| 31 | 00011111 |
| 32 | 00100000 |
| 33 | 00100001 |
| 34 | 00100010 |
| 35 | 00100011 |
| 36 | 00100100 |
| 37 | 00100101 |
| 38 | 00100110 |
| 39 | 00100111 |
| 40 | 00101000 |
| 41 | 00101001 |
| 42 | 00101010 |
| 43 | 00101011 |
| 44 | 00101100 |
| 45 | 00101101 |
| 46 | 00101110 |
| 47 | 00101111 |
| 48 | 00110000 |
| 49 | 00110001 |
| 50 | 00110010 |
| 51 | 00110011 |
| 52 | 00110100 |
| 53 | 00110101 |
| 54 | 00110110 |
| 55 | 00110111 |
| 56 | 00111000 |
| 57 | 00111001 |
| 58 | 00111010 |
| 59 | 00111011 |
| 60 | 00111100 |
| 61 | 00111101 |
| 62 | 00111110 |
| 63 | 00111111 |
| 64 | 01000000 |
| Decimal | Binary |
|---|---|
| 65 | 01000001 |
| 66 | 01000010 |
| 67 | 01000011 |
| 68 | 01000100 |
| 69 | 01000101 |
| 70 | 01000110 |
| 71 | 01000111 |
| 72 | 01001000 |
| 73 | 01001001 |
| 74 | 01001010 |
| 75 | 01001011 |
| 76 | 01001100 |
| 77 | 01001101 |
| 78 | 01001110 |
| 79 | 01001111 |
| 80 | 01010000 |
| 81 | 01010001 |
| 82 | 01010010 |
| 83 | 01010011 |
| 84 | 01010100 |
| 85 | 01010101 |
| 86 | 01010110 |
| 87 | 01010111 |
| 88 | 01011000 |
| 89 | 01011001 |
| 90 | 01011010 |
| 91 | 01011011 |
| 92 | 01011100 |
| 93 | 01011101 |
| 94 | 01011110 |
| 95 | 01011111 |
| 96 | 01100000 |
| 97 | 01100001 |
| 98 | 01100010 |
| 99 | 01100011 |
| 100 | 01100100 |
| 101 | 01100101 |
| 102 | 01100110 |
| 103 | 01100111 |
| 104 | 01101000 |
| 105 | 01101001 |
| 106 | 01101010 |
| 107 | 01101011 |
| 108 | 01101100 |
| 109 | 01101101 |
| 110 | 01101110 |
| 111 | 01101111 |
| 112 | 01110000 |
| 113 | 01110001 |
| 114 | 01110010 |
| 115 | 01110011 |
| 116 | 01110100 |
| 117 | 01110101 |
| 118 | 01110110 |
| 119 | 01110111 |
| 120 | 01111000 |
| 121 | 01111001 |
| 122 | 01111010 |
| 123 | 01111011 |
| 124 | 01111100 |
| 125 | 01111101 |
| 126 | 01111110 |
| 127 | 01111111 |
| 128 | 10000000 |
| Decimal | Binary |
|---|---|
| 129 | 10000001 |
| 130 | 10000010 |
| 131 | 10000011 |
| 132 | 10000100 |
| 133 | 10000101 |
| 134 | 10000110 |
| 135 | 10000111 |
| 136 | 10001000 |
| 137 | 10001001 |
| 138 | 10001010 |
| 139 | 10001011 |
| 140 | 10001100 |
| 141 | 10001101 |
| 142 | 10001110 |
| 143 | 10001111 |
| 144 | 10010000 |
| 145 | 10010001 |
| 146 | 10010010 |
| 147 | 10010011 |
| 148 | 10010100 |
| 149 | 10010101 |
| 150 | 10010110 |
| 151 | 10010111 |
| 152 | 10011000 |
| 153 | 10011001 |
| 154 | 10011010 |
| 155 | 10011011 |
| 156 | 10011100 |
| 157 | 10011101 |
| 158 | 10011110 |
| 159 | 10011111 |
| 160 | 10100000 |
| 161 | 10100001 |
| 162 | 10100010 |
| 163 | 10100011 |
| 164 | 10100100 |
| 165 | 10100101 |
| 166 | 10100110 |
| 167 | 10100111 |
| 168 | 10101000 |
| 169 | 10101001 |
| 170 | 10101010 |
| 171 | 10101011 |
| 172 | 10101100 |
| 173 | 10101101 |
| 174 | 10101110 |
| 175 | 10101111 |
| 176 | 10110000 |
| 177 | 10110001 |
| 178 | 10110010 |
| 179 | 10110011 |
| 180 | 10110100 |
| 181 | 10110101 |
| 182 | 10110110 |
| 183 | 10110111 |
| 184 | 10111000 |
| 185 | 10111001 |
| 186 | 10111010 |
| 187 | 10111011 |
| 188 | 10111100 |
| 189 | 10111101 |
| 190 | 10111110 |
| 191 | 10111111 |
| 192 | 11000000 |
| Decimal | Binary |
|---|---|
| 193 | 11000001 |
| 194 | 11000010 |
| 195 | 11000011 |
| 196 | 11000100 |
| 197 | 11000101 |
| 198 | 11000110 |
| 199 | 11000111 |
| 200 | 11001000 |
| 201 | 11001001 |
| 202 | 11001010 |
| 203 | 11001011 |
| 204 | 11001100 |
| 205 | 11001101 |
| 206 | 11001110 |
| 207 | 11001111 |
| 208 | 11010000 |
| 209 | 11010001 |
| 210 | 11010010 |
| 211 | 11010011 |
| 212 | 11010100 |
| 213 | 11010101 |
| 214 | 11010110 |
| 215 | 11010111 |
| 216 | 11011000 |
| 217 | 11011001 |
| 218 | 11011010 |
| 219 | 11011011 |
| 220 | 11011100 |
| 221 | 11011101 |
| 222 | 11011110 |
| 223 | 11011111 |
| 224 | 11100000 |
| 225 | 11100001 |
| 226 | 11100010 |
| 227 | 11100011 |
| 228 | 11100100 |
| 229 | 11100101 |
| 230 | 11100110 |
| 231 | 11100111 |
| 232 | 11101000 |
| 233 | 11101001 |
| 234 | 11101010 |
| 235 | 11101011 |
| 236 | 11101100 |
| 237 | 11101101 |
| 238 | 11101110 |
| 239 | 11101111 |
| 240 | 11110000 |
| 241 | 11110001 |
| 242 | 11110010 |
| 243 | 11110011 |
| 244 | 11110100 |
| 245 | 11110101 |
| 246 | 11110110 |
| 247 | 11110111 |
| 248 | 11111000 |
| 249 | 11111001 |
| 250 | 11111010 |
| 251 | 11111011 |
| 252 | 11111100 |
| 253 | 11111101 |
| 254 | 11111110 |
| 255 | 11111111 |
Преобразование шестнадцатеричного числа в десятичное
Для начала, небольшой рисунок:
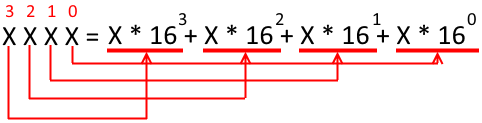
Для преобразования требуется каждую цифру числа умножить на «разряд», в котором оно находится. Из курса начальной школы мы помним, что позиции, занимаемые в числовой строке, называются (справа налево) единицы, десятки, сотни и т. д. Здесь почти то же самое, но с поправкой на систему счисления. Каждый следующий разряд — это +1 степень текущей системы счисления. Любое число в степени ноль — это ноль, в степени 1 — самом число, в степени 2 (квадрат) — число, умноженное само на себя и т. д.
Для наглядности привожу пример. Допустим, возьмём шестнадцатеричное число 0x1F8. Нам требуется перевести его в десятичную систему, поэтому запишем (0x — это признак основания!):
1F816 = 116 × 162 + F16 × 161 + 816 × 16 = 1 × 256 + 15 × 16 + 8 × 1 = 256 + 240 + 8 = 504
Обе таблички нам пригодились: благодаря второй мы переводим числа из шестнадцатеричной системы в десятичную, благодаря первой — легко перемножаем «больше» числа.
Небольшое отступление
А знаете ли вы, что у нас сейчас могла бы использоваться двенадцатеричная система счисления, используемая ещё шумерцами? По одной и версий, этому способствовало количество фаланг пальцев руки. Взгляните на рисунок:
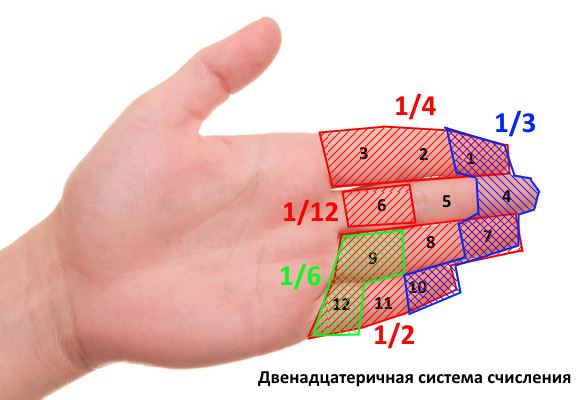
Скорее всего, вам сложно это представить. Но, взглянув на это под другим углом, можем убедиться, что выбор был бы очень хорош, ведь 12 делится без остатка на 2, 3, 4, 6 (в то время, как 10 можно разделить лишь на 2 и 5). Естественно, умножения и деления на степень числа 12 были так же просты, как сейчас аналогичные операции для степени числа 10.
Выучив эти таблицы, любой человек легко сможет переводить компьютерные байты в привычные числа. При желании, как следует потренировавшись и «расширив объём» краткосрочной памяти, станут доступны и более сложные варианты. Но, как уже говорилось чуть ранее, манипуляции с байтами мало кому нужны, не говоря о чём-то большем.
Поддержка сайта
С удовольствием создаю годный контент. Буду очень признателен, если вы поддержите мои усилия:
днём интернета
шоколадкой для работы мозга
коробочкой ароматного чая для бодрости
продлением хостинга на +1 месяц
2 070
не в сети 4 дня
What is a hex number?
A hex number, short for hexadecimal number, is a number expressed in the hexadecimal positional numeral system with a base of 16 which uses sixteen symbols: the numbers from 0 to 9 and the letters A,B,C,D,E, and F, to represent values from 0 to 15. Equivalently, small-case letters a through f can be used. For example, 10 in decimal is A in hex, 100 in decimal is 64 in hex, while 1,000 in decimal is 3E8 in hex. Hex numbers have signs, just like decimal ones, for example -1e is equal to -30 in decimal.
Hex numerals are used mostly in computing: computer system designers, software engineers and programmers as a convenient representation of the underlying binary systems. People in such occupations are most likely to be in need of a hex calculator or hex converter.
An ordinary person would encounter them every day when browsing the web since in website addresses (URLs) special characters are encoded as a hex numeral, e.g. %20 stands for «space» (blank). A lot of webpages also encode special characters in html in terms of their hexadecimal numerical character reference (code), e.g. ’ is the Unicode for a single quotation mark (’). A regular person browsing the web should not require a hexadecimal converter or calculator to do so.
Using our hex calculator, you can perform arithmetic operations (addition, subtraction, multiplication and division of hex numbers) as well as use it as a hex converter for hex to decimal, decimal to hex, hex to binary and binary to hex conversions.
Here is a table of some numbers represented in the decimal, hex and binary systems (base 10, base 2 and base 16).
| Decimal | Hex | Binary |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 10 |
| 3 | 3 | 11 |
| 5 | 5 | 101 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
| 50 | 32 | 110010 |
| 63 | 3F | 111111 |
| 100 | 64 | 1100100 |
| 1000 | 3E8 | 1111101000 |
| 10000 | 2710 | 10011100010000 |
Таблица соответствия шестнадцатеричных цифр
| HEX (шестнадцатеричная) | DEC (десятичная) |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
А теперь вспомним поразрядное умножение из предыдущей статьи, для цифры 7. Здесь будет лишь поправка на другую систему счисления (не на 10, как там, а на 16).
Обычно в компьютерной литературе, для однозначного указания основания системы счисления, применяется следующая нотация:
— шестнадцатеричное число — 0x100 (256 в десятичной, признак — 0x в начале)
— десятичное число — 100 (наша, человеческая, система счисления)
— восьмеричное число — 0100 (64 в десятичной, признак — ведущий ноль)
— двоичное число — 0b100 (4 в десятичной, признак — 0b в начале)
Хакерский редактор Hacker Viewer (Hiew) .
Для визуального восприятия шестнадцатеричного кода воспользуемся замечательным простым, но достаточно функциональным DOS редактором Hacker Viewer (Hiew). Вы найдёте его в папке D:\UTILS\HIEW\ (я надеюсь, что наш архив программ DOS-1.rar уже скачан и DOSBox установлен и запущен).
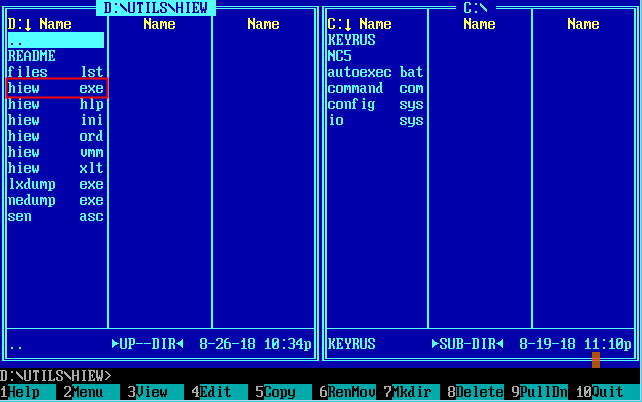 Запускаем HIEW (Hacker Viewer).
Запускаем HIEW (Hacker Viewer).
Инструкцию по пользованию Hiew для хакеров от Криса Касперского вы найдёте в папочке readme. Пользоваться редактором просто и удобно.
Откроем с помощью Hiew нашу программу PRG.COM (выбор файлов — F9). При помощи F4 выбираем режим отображения информации HEX (как вы уже знаете, шестнадцатеричный режим). Можете с помощью F4 или Enter по переключаться между режимами отображения.
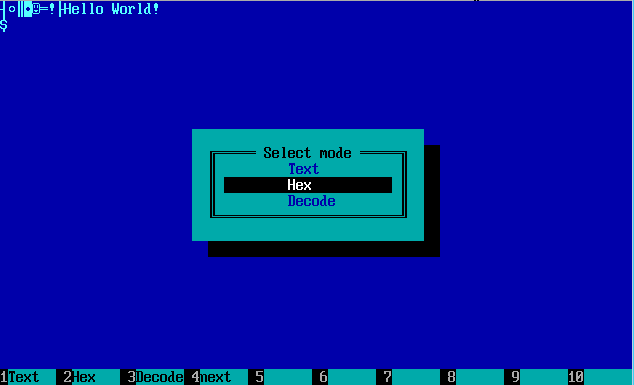 Переключение режимов отображения в Hacker Viewer.
Переключение режимов отображения в Hacker Viewer.
Обратите внимание на положение Decode (декодирование). Вам это ни о чём не говорит? Да, да, да в Hiew имеется встроенный дизассемблер и даже ассемблер! Можно внести изменения в ассемблерный код, не выходя из редактора и сохранить изменения.
Исполняемый файл останется рабочим — гениальная программа с поразительными возможностями для своего времени!. Подобное отображение HEX системы счисления вы увидите практически во всех отладочных программах и просмотрщиках файлов.
Перемещайте курсор с помощью клавиш стрелок на клавиатуре
Вверху вы заметите изменение цифры указателя (pointer)
Подобное отображение HEX системы счисления вы увидите практически во всех отладочных программах и просмотрщиках файлов.
Перемещайте курсор с помощью клавиш стрелок на клавиатуре. Вверху вы заметите изменение цифры указателя (pointer).
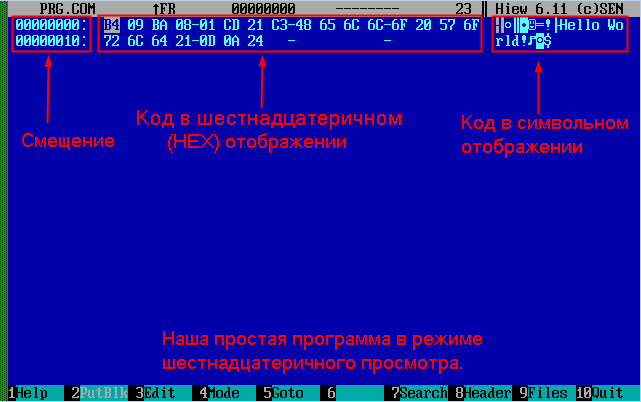 Наша первая программа в шестнадцатеричном виде.
Наша первая программа в шестнадцатеричном виде.
Указатель является одним из основополагающих понятий в системе программирования. Основы понимания работы с указателем рассмотрим попозже.
Converting to and from hex numerals
Converting numbers to and from hex does not change the number itself, it just changes its form. Using our hex converter above, you can do both types of conversions quickly and easily. Note that hex conversion and hex calculation are separate operations and you do not need to perform one in order to perform the other.
Hex to decimal
Each position in a hexadecimal numeral represents a power of 16 the same way each position in a decimal number represents a power of 10. For example, the number 20 in decimal is 2 · 101 + 0 · 10 = 20. The hex number 20 is then 2 · 161 + 0 · 16 = 32 in dec. Similarly, the number 1E is 1 · 16 + 14 · 1 = 30 in decimal.
The process of hex to decimal conversion is therefore to first take each position and convert it to decimal, e.g. 9 is 9, but B is converted to 11, then to multiply each position by 16 to the power of the position number, counting from right to left and starting at zero. If you need to calculate large exponents like 168 you might find our exponent calculator useful.
Decimal to hex
This process is a bit more complex as we are going from a higher base to a lower base. Let us say the number we want to convert from decimal to hex is X. Begin by finding the largest power of 16 ≤ X and denote it by E. Then determine how many times the power of 16 found above goes into X, denote it by Z1. Denote the remainder by Y1.
Repeat the above steps using Yn as a starting value until 16 is larger than the remaining value and assign the remainder to the 16 position, then assign each of the values Y1…n to its respective position and you will have your hex value.
Example dec to hex conversion: Convert 1000 in decimal to hex.
1.) Largest power E = 2 (162 = 256 ≤ 1000, 163 = 4,096 ≥ 1000)
2.) Z1 = 1000 / 162 = 3 (232 remainder); Y1 = 232
3.) Largest power E = 1 (161 = 16 ≤ 232, 162 = 256 ≥ 232)
4.) Z2 = 232 / 161 = 14 (8 remainder); Y2 = 8
5.) 8 < 16; Z3 = 8, end.
Combine Z1..n to get 3E8 (14 dec = E hex). You can verify the result using our hex converter.
Hex to decimal and decimal to hex conversion follows the same principles, but with base 2 instead of base 10.
Decimal System
The decimal numeral system is the most commonly used and the standard system in daily life. It uses the number 10 as its base (radix). Therefore, it has 10 symbols: The numbers from 0 to 9; namely 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
As one of the oldest known numeral systems, the decimal numeral system has been used by many ancient civilizations. The difficulty of representing very large numbers in the decimal system was overcome by the Hindu–Arabic numeral system. The Hindu-Arabic numeral system gives positions to the digits in a number and this method works by using powers of the base 10; digits are raised to the nth power, in accordance with their position.
For instance, take the number 2345.67 in the decimal system:
- The digit 5 is in the position of ones (10, which equals 1),
- 4 is in the position of tens (101)
- 3 is in the position of hundreds (102)
- 2 is in the position of thousands (103)
- Meanwhile, the digit 6 after the decimal point is in the tenths (1/10, which is 10-1) and 7 is in the hundredths (1/100, which is 10-2) position
- Thus, the number 2345.67 can also be represented as follows:
(2 * 103) + (3 * 102) + (4 * 101) + (5 * 10) + (6 * 10-1) + (7 * 10-2)
Hexadecimal to Decimal Conversion Chart
| Hexadecimal | Decimal |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
| 10 | 16 |
| 11 | 17 |
| 12 | 18 |
| 13 | 19 |
| 14 | 20 |
| 15 | 21 |
| 16 | 22 |
| 17 | 23 |
| 18 | 24 |
| 19 | 25 |
| 1A | 26 |
| 1B | 27 |
| 1C | 28 |
| 1D | 29 |
| 1E | 30 |
| 1F | 31 |
| 20 | 32 |
| 21 | 33 |
| 22 | 34 |
| 23 | 35 |
| 24 | 36 |
| 25 | 37 |
| 26 | 38 |
| 27 | 39 |
| 28 | 40 |
| 29 | 41 |
| 2A | 42 |
| 2B | 43 |
| 2C | 44 |
| 2D | 45 |
| 2E | 46 |
| 2F | 47 |
| 30 | 48 |
| 31 | 49 |
| 32 | 50 |
| 33 | 51 |
| 34 | 52 |
| 35 | 53 |
| 36 | 54 |
| 37 | 55 |
| 38 | 56 |
| 39 | 57 |
| 3A | 58 |
| 3B | 59 |
| 3C | 60 |
| 3D | 61 |
| 3E | 62 |
| 3F | 63 |
| 40 | 64 |
| Hexadecimal | Decimal |
|---|---|
| 41 | 65 |
| 42 | 66 |
| 43 | 67 |
| 44 | 68 |
| 45 | 69 |
| 46 | 70 |
| 47 | 71 |
| 48 | 72 |
| 49 | 73 |
| 4A | 74 |
| 4B | 75 |
| 4C | 76 |
| 4D | 77 |
| 4E | 78 |
| 4F | 79 |
| 50 | 80 |
| 51 | 81 |
| 52 | 82 |
| 53 | 83 |
| 54 | 84 |
| 55 | 85 |
| 56 | 86 |
| 57 | 87 |
| 58 | 88 |
| 59 | 89 |
| 5A | 90 |
| 5B | 91 |
| 5C | 92 |
| 5D | 93 |
| 5E | 94 |
| 5F | 95 |
| 60 | 96 |
| 61 | 97 |
| 62 | 98 |
| 63 | 99 |
| 64 | 100 |
| 65 | 101 |
| 66 | 102 |
| 67 | 103 |
| 68 | 104 |
| 69 | 105 |
| 6A | 106 |
| 6B | 107 |
| 6C | 108 |
| 6D | 109 |
| 6E | 110 |
| 6F | 111 |
| 70 | 112 |
| 71 | 113 |
| 72 | 114 |
| 73 | 115 |
| 74 | 116 |
| 75 | 117 |
| 76 | 118 |
| 77 | 119 |
| 78 | 120 |
| 79 | 121 |
| 7A | 122 |
| 7B | 123 |
| 7C | 124 |
| 7D | 125 |
| 7E | 126 |
| 7F | 127 |
| 80 | 128 |
| Hexadecimal | Decimal |
|---|---|
| 81 | 129 |
| 82 | 130 |
| 83 | 131 |
| 84 | 132 |
| 85 | 133 |
| 86 | 134 |
| 87 | 135 |
| 88 | 136 |
| 89 | 137 |
| 8A | 138 |
| 8B | 139 |
| 8C | 140 |
| 8D | 141 |
| 8E | 142 |
| 8F | 143 |
| 90 | 144 |
| 91 | 145 |
| 92 | 146 |
| 93 | 147 |
| 94 | 148 |
| 95 | 149 |
| 96 | 150 |
| 97 | 151 |
| 98 | 152 |
| 99 | 153 |
| 9A | 154 |
| 9B | 155 |
| 9C | 156 |
| 9D | 157 |
| 9E | 158 |
| 9F | 159 |
| A0 | 160 |
| A1 | 161 |
| A2 | 162 |
| A3 | 163 |
| A4 | 164 |
| A5 | 165 |
| A6 | 166 |
| A7 | 167 |
| A8 | 168 |
| A9 | 169 |
| AA | 170 |
| AB | 171 |
| AC | 172 |
| AD | 173 |
| AE | 174 |
| AF | 175 |
| B0 | 176 |
| B1 | 177 |
| B2 | 178 |
| B3 | 179 |
| B4 | 180 |
| B5 | 181 |
| B6 | 182 |
| B7 | 183 |
| B8 | 184 |
| B9 | 185 |
| BA | 186 |
| BB | 187 |
| BC | 188 |
| BD | 189 |
| BE | 190 |
| BF | 191 |
| C0 | 192 |
| Hexadecimal | Decimal |
|---|---|
| C1 | 193 |
| C2 | 194 |
| C3 | 195 |
| C4 | 196 |
| C5 | 197 |
| C6 | 198 |
| C7 | 199 |
| C8 | 200 |
| C9 | 201 |
| CA | 202 |
| CB | 203 |
| CC | 204 |
| CD | 205 |
| CE | 206 |
| CF | 207 |
| D0 | 208 |
| D1 | 209 |
| D2 | 210 |
| D3 | 211 |
| D4 | 212 |
| D5 | 213 |
| D6 | 214 |
| D7 | 215 |
| D8 | 216 |
| D9 | 217 |
| DA | 218 |
| DB | 219 |
| DC | 220 |
| DD | 221 |
| DE | 222 |
| DF | 223 |
| E0 | 224 |
| E1 | 225 |
| E2 | 226 |
| E3 | 227 |
| E4 | 228 |
| E5 | 229 |
| E6 | 230 |
| E7 | 231 |
| E8 | 232 |
| E9 | 233 |
| EA | 234 |
| EB | 235 |
| EC | 236 |
| ED | 237 |
| EE | 238 |
| EF | 239 |
| F0 | 240 |
| F1 | 241 |
| F2 | 242 |
| F3 | 243 |
| F4 | 244 |
| F5 | 245 |
| F6 | 246 |
| F7 | 247 |
| F8 | 248 |
| F9 | 249 |
| FA | 250 |
| FB | 251 |
| FC | 252 |
| FD | 253 |
| FE | 254 |
| FF | 255 |
Три системы счисления.
Практическое программирование на ассемблере требует понимания системы счисления. Систем счисления существует бесконечное множество. Наиболее знакомая для нас — десятичная система счисления. Римская нумерация циферблата часов демонстрирует нам двенадцатеричную систему счисления. Программистам на ассемблере необходимо освоить три системы счисления : десятичную, двоичную и шестнадцатеричную.
Машина «думает» байтами. Байт состоит из 8 бит. Бит может содержать одно значение: 0 или 1. Так что в принципе, неплохо иметь представление и о восьмеричной системе счисления.Однако машинный код отображается в различных редакторах в виде шестнадцатеричного значения — оно более удобно для восприятия, так что всё же остановимся на трёх обязательно необходимых программисту системах счисления.