Длина волны

Содержание:

Радиоволны: свойства и применение
- Основные параметры радиоволн
- Свойства и применение
Примеры
Длина волны в среде
Примечание к расчетам табличных формул
Определение и формула длины волн
В квантовой теории поля
Определения и формулы
Фазовая скорость — радиоволна
Что такое radiowave и ее характеристики?
Виды волн
Синусоидальные волны
Скорость звуковых волн в различных средах
Приведённая комптоновская длина волны

Радиоволны: свойства и применение

Радиоволной называется электромагнитное излучение, длины волн которого варьируются от 5*10-5 до 1010 метров. Стоит подробнее поговорить об основных параметрах радиоволн, которые ограничивают сферу их применения в современной науке и технике.

Основные параметры радиоволн

Среди основных параметров радиоволн следует выделить следующие:

радиочастотный спектр. Это совокупность всех частот, которые установлены международными стандартами связи. Они могут быть использованы для функционирования радиоэлектронных средств и средств связи;
радиочастота. Это та частота, которая установлена для обозначения единичной составляющей радиочастотного спектра;
распределение полос радиочастот. То есть для каждого конкретного подразделения и вида деятельности выделяется отдельная частота, на которой эта служба работает.

Эти параметры радиоволн могут различаться для каждого конкретного случая.

Свойства и применение

Стоит поговорить подробнее об основных свойствах радиоволн. К ним можно отнести:

все радиоволны распространяются в однородной среде прямолинейно. При этом их скорость напрямую будет зависеть от плотности среды, в которой они распространяются;
если радиоволна распространяется в среде отличной от воздуха, то этот процесс сопровождается поглощением энергии;
если радиоволна переходит из одной среды в другую, то она преломляется и отражается;
если радиоволна распространяется в неоднородной среде, то ее траектория искажается;
радиоволнам свойственна дифракция, то есть огибание препятствий встречающихся на пути;
им свойственна интерференция, то есть сложение двух волн одной и той же частоты, которые созданы одним источником.

Теперь можно поговорить о применение радиоволн в современной технике.

Радиоволны широко распространены в радиолокации. Благодаря такому устройству можно наблюдать за предметами на большом расстоянии.

Благодаря радиоволнам у человечества появилась возможность передавать данные на огромные расстояния, при этом не нужно тянуть никаких кабелей. Радиоволны в настоящее время находят широкое распространение при различных исследования во врачебном деле. На их основе делаются различные установки, которые позволяют не только производить обследование человеческого тела, но и лечить его от различных болезней.

Не будь радиоволн, ни один человек никогда бы не узнал, что такое телевидение и радио. Именно они несут сигнал различных частот, которые затем воспринимаются антеннами и спутниковыми тарелками.

Оборонная промышленность очень сильно зависит от радиоволн. Они позволяют настраивать связь на огромных расстояниях, а также используются для наведения на цель.

Освещение очень важно для нормальной жизни и работы. При этом освещение с помощью солнца не всегда доступно по понятным причинам, поэтому часто используется искусственное освещение

Для того, чтобы уразуметь понятие «сила тока», нужно знать что из себя представляет электрический ток.

Коэффициент стоячей волны (иначе КСВ) – один из показателей, характеризующий свойства стоячей волны в каком-либо поле.

Примеры

Колебательный контур

Видеоурок: длина волны

Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 делим на частоту в мегагерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару f λ, например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц, можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц 3 м × 100 = 300 м

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм.

Длина волны в среде

Модулятор тв сигнала

В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.

Длина электромагнитной волны в среде короче, чем в вакууме:

λ=cnν,{\displaystyle \lambda ={\frac {c}{n\nu }},}

где n=εμ>1{\displaystyle n={\sqrt {\varepsilon \mu }}>1} — показатель преломления среды;

ε{\displaystyle \varepsilon } — относительная диэлектрическая проницаемость среды;

μ{\displaystyle \mu } — относительная магнитная проницаемость среды.

Величины n{\displaystyle n}, μ{\displaystyle \mu } и ε{\displaystyle \varepsilon } могут существенно зависеть от частоты ν{\displaystyle \nu } (явление дисперсии). Поскольку для большинства сред в радиочастотном диапазоне μ≈1{\displaystyle \mu \approx 1} (для диэлектриков μ=1{\displaystyle \mu =1}, для ферромагнетиков с ростом частоты μ→1{\displaystyle \mu \rightarrow 1}), то в инженерной практике используют величину 1ε<1{\displaystyle 1/{\sqrt {\varepsilon }}<1}, которую называют коэффициентом укорочения. Она равна отношению длины волны в среде к длине волны в вакууме. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) ε{\displaystyle \varepsilon } = 2,56, и коэффициент укорочения 1ε{\displaystyle 1/{\sqrt {\varepsilon }}} = 1/1,6 = 0,625.

Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением ε{\displaystyle \varepsilon }, но и больше, чем вакууме, поскольку фазовая скорость электромагнитной волны в волноводе превышает скорость электромагнитной волны в среде с тем же ε{\displaystyle \varepsilon }.

Примечание к расчетам табличных формул

Вибратор герца

Значение скорости света / волны
примерное = 300000 км/сек
точное = 299792458 м/с.

В качестве разделителя / запятой — используется точка.

Калькулятор может применяться для расчета радиоантенн, телевизионных, радиолюбительских и радиотехнических расчетов.

Для исследования диапазона frequency antenna следует ввести длину излучателя радиоволн в калькулятор.
Если, известно, что преобразователь энергии эфира λ/2 — следует умножить длину электромагнитного конвертера на 2 перед вводом в калькулятор.
Если, λ/4 — то умножить на 4, и так далее …

Так, как при расчете N-полюсника излучения могут использоваться нестандартные значения, становиться невозможным изначально установить, на какой диапазон количества повторений за единицу времени настроена антенна …
Поэтому, ниже информационного сообщения будут расчитаны диапазоны числа колебаний в секунду для различных нестандартных значений …
Используйте эти значения, как справочные (для диапазона MHz), если делитель λ неизвестен …

Зачем ? Почему ? Для Чего ? используют λ/2 , λ/4 значения от целой длины antenna ? Да, потому, что эффективность обычного диполя λ/2 = 100% … Если достаточно половинного размера для достижения 100% эффективности радиоантенны — почему бы не сэкономить на дорогостоящих цвет / мет материалах, а также на весе и парусности всей конструкции, удобстве монтажа и ориентирования, меньшего ущерба в случае падения ? Все — просто … Просто — достаточно …

Определение и формула длины волн

Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.

Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

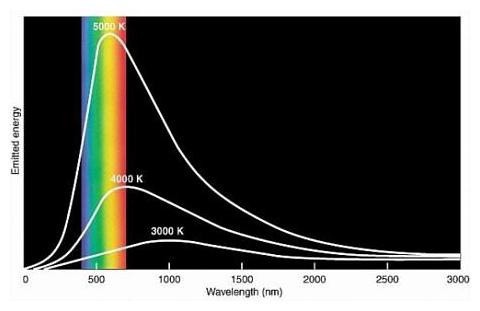
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

В квантовой теории поля

Частица, локализованная в области с линейными размерами не более λ_C, согласно соотношению неопределённостей имеет квантовомеханическую неопределённость в импульсе не менее mc и неопределённость в энергии не менее mc², что достаточно для рождения пар частиц-античастиц с массой m. В такой области элементарная частица, вообще говоря, уже не может рассматриваться как «точечный объект», потому что часть времени она проводит в состоянии «частица + пары». В результате на расстояниях, меньших λ_C, частица выступает как система с бесконечным числом степеней свободы и её взаимодействия должны описываться в рамках квантовой теории поля — в этом фундаментальная роль параметра λ_C, определяющего минимальную погрешность, с которой может быть измерена координата частицы в её системе покоя. В частности, переход в промежуточное состояние «частица + пары», осуществляющийся за время ~λ/с, характерное для рассеяния света с длиной волны λ, при λ ≤ λ_C приводит к нарушению законов классической электродинамики в комптон-эффекте.

В действительности во всех случаях размер области, где частица перестаёт быть «точечным объектом», зависит не только от её комптоновской длины, но и от комптоновских длин других частиц, в которые данная частица может динамически превращаться. Но, например, для лептонов, не обладающих сильным взаимодействием, переход в другие состояния маловероятен (можно сказать, что он происходит редко или требует большого времени). Поэтому лептонная «шуба» из пар является как бы прозрачной, и во многих задачах лептоны с хорошей точностью могут рассматриваться как «точечные частицы». Для тяжёлого адрона, например нуклона N, эффективный размер области, где начинает проявляться «шуба», значительно больше комптоновской длины нуклона и определяется комптоновской длиной самого лёгкого из адронов — пиона π (заметим, что λπC ≈ 7λNC). В области с линейным размером порядка λπC нуклоны с большой интенсивностью (из-за сильного взаимодействия) переходят в промежуточные состояния «нуклон + пионы», поэтому нуклонная «шуба», в отличие от лептонной, плотная.

Таким образом, эффективная область, где частица перестаёт проявляться как «точечная», определяется не только соответствующими комптоновскими длинами волн, но и константами взаимодействия данной частицы с другими частицами (полями).

Определения и формулы

Звук — это волновой процесс. Если струна скрипки или арфы колеблется, в окружающем ее воздуха образуются зоны сжатия и разрежения, которые и представляют собой звук. Эти зоны сжатия и разрежения перемещаются по воздуху в форме продольных волн, которые имеют ту же частоту, что и источник звука. В продольных волнах молекулы воздуха движутся параллельно движению волны. Воздух сжимается в том же направлении, в котором распространяются звуковые волны. Эти волны передают энергию голоса или колеблющейся струны. Отметим, что воздух не перемещается, когда звуковая волна проходит через него. Перемещаются только колебания, то есть зоны сжатия и разрежения. Более громкие звуки получаются при более сильных сжатиях и разрежениях.

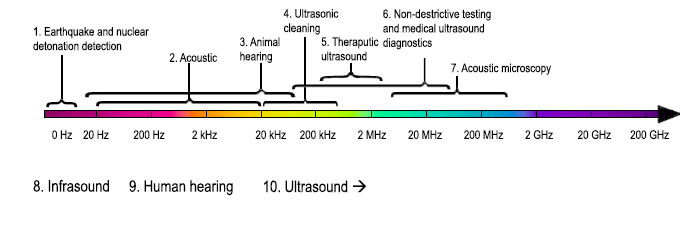Спектр звуковых колебаний. 1 — землетрясения, молнии и обнаружение ядерных взрывов; 2 — акустический диапазон; 3 — Слух животных; 4, Ультразвуковая очистка; 5. Терапевтическое применение ультразвука; 6 — Неразрушающий контроль и медицинская ультразвуковая диагностика; 7 — Акустическая микроскопия; 8 — Инфразвук; 9 — Слышимый диапазон; 10 — Ультразвук

Количество этих колебаний в секунду называется частотой и измеряется в герцах. Период колебаний — это длительность одного цикла колебаний, измеренная в секундах. Длина волны — это расстояние между двумя соседними повторяющимися зонами волнового процесса. Если предположить, что скорость распространения волны в среде постоянная, то длина волны обратно пропорциональна частоте.

При 20 °C звук распространяется в сухом воздухе со скоростью около 343 метра в секунду или 1 километр приблизительно за 3 секунды. Звук распространяется быстрее в жидкостях и еще быстрее в твердых телах. Например, в воде звук распространяется в 4,3 раза быстрее, чем в воздухе, в стекле — в 13 раз и в алмазе в 35 раз быстрее, чем в воздухе.

Хотя звуковые волны и морские волны движутся намного медленнее электромагнитных волн, уравнение, описывающее их движение будет одинаковым для всех трех типов волн:

или

где

f — частота волны,

v — скорость распространения волны и

λ — длина волны

Фазовая скорость — радиоволна

Фазовая скорость радиоволн, распространяющихся вдоль земной поверхности ( земных волн) вблизи излучателя, зависит от ее электрических свойств.

Зависимость множителя ослабления W от параметра р.| Границы применимости формулы ( 3 — 24.

Фазовая скорость радиоволны, распространяющейся вблизи земной поверхности, зависит от ее электрических параметров. При переходе радиоволны с моря на сушу ( вблизи береговой линии) происходит изменение направления распространения волны, называемое береговой рефракцией. Это создает ошибку в определении направления прихода радиоволн, что существенно для работы радионавигационных систем.

Флуктуации фазовой скорости радиоволн на трассе распространения сигналов точного времени не позволяют использовать принятые сигналы для точных измерений частоты за короткие промежутки времени. Чем больше величина случайных изменений фазы на трассе распространения радиоволн, тем больший интервал времени необходим для измерения. На погрешность сличения частот влияют также систематические изменения в атмосфере на трассе распространения при восходе и заходе солнца.

Линзовые антенны.

Так как относительная диэлектрическая проницаемость диэлектрика больше единицы, то фазовая скорость радиоволн, проходящих через линзу, уменьшается по сравнению со скоростью в воздухе. Зато лучи 2 и 3 затрачивают большее время на пути до линзы. Таким образом, наряду с преломлением радиоволн на границе воздух — диэлектрик на входе линзы, изменяющим-направление хода лучей, происходит выравнивание фаз.

Как же влияет ионизация атмосферы на распространение радиоволн. Уменьшение диэлектрической проницаемости атмосферы означает увеличение фазовой скорости радиоволн при перехо де их из нижних слоев атмосферы в ионосферу, а это влечет за собой преломление и отражение волн.

Поэтому фаза вынужденных колебаний электронов совпадает с фазой приходящей волны, т.е. имеет место первый из рассмотренных выше случаев — фазовая скорость радиоволн в диэлектрике всегда меньше, чем в вакууме.

Распространение ДВ и СДВ в волноводе Земля — ионосфера.

Как и во всяком волноводе, можно отметить оптимальные волны — волны, распространяющиеся с наименьшим затуханием, и критическую волну. Для волновода, образованного Землей и ионосферой, оптимальными являются волны длиной 25 — 35 км, а критической — волна длиной 100 км. Подобно законам распространения радиоволн в обычных волноводах, в сферическом ионосферном волноводе фазовая скорость радиоволн превышает скорость света в свободном пространстве. Однако фазовая скорость изменяется с изменением расстояния от передатчика. Кроме того, она зависит от электронной плотности и числа столкновений электронов с молекулами в той области ионосферы, где происходит отражение радиоволн.

Если электроны среды не удерживаются в определенных положениях упругими силами, как это имеет место в диэлектрике, а являются свободными, то частота их собственных колебаний обращается в пуль. Поэтому частота радиоволн всегда выше, чем собственная частота колебаний свободных электронов, вследствие чего вынужденные колебания электронов по фазе противоположны приходящей волне. Следовательно, в пространстве, содержащем свободные электроны, в частности в ионосфере, имеет места второй рассмотренный случай — фазовая скорость радиоволн больше, чем в вакууме.

Наоборот, когда фаза вынужденных колебаний электронов противоположна по фазе приходящей волне, то длина волны и фазовая скорость в среде больше, чем т вакууме. Если электроны среды не удерживаются в определенных положениях упругими силами, как это имеет место в диэлектрике, а являются свободными, то частота их собственных колебаний обращается в нуль. Поэтому частота радиоволн всегда выше, чем собственная частота колебаний свободных электронов, вследствие чего вынужденные колебания электронов по фазе противоположны приходящей волне. Следовательно, в пространстве, содержащем свободные электроны, в частности в ионосфере, имеет место второй рассмотренный случай — фазовая скорость радиоволн больше, чем в вакууме.

Что такое radiowave и ее характеристики?

Природа, в понятии суть Вселенной — не любит прямых углов … Нет, конечно — природа не избегает, однозначно, прямых углов и острых граней в строительстве мира … Но, ее живая, в постоянном движении, структура — истирает грани до округлости … Ээлектромагнитные колебания, базирующиеся на волновой структуре природы — полностью повторяют все ее многообразие … Electromagnetic oscillation — одно из самых известных и не изученных до конца (не классифицированных) явлений мироздания … Двигаясь, из точки рождения — возмущение среды с переносом энергии совершает равноудаленные колебательные движения, синхронизированные скоростью ее распространения … Волновые зависимости скорости, частоты и длины отражены описанием математической формулы …

Исходя из многообразия, длина волны λ также имеет множественные определения :
— как, кратчайшее расстояние между двумя точками колебания в одинаковой фазе …
— как, изменение фазы колебаний волны на 2π (где, 2π — не что иное, как — круг) …
— как, путь фронта волны, равный периоду колебательного процесса …
Длина радиоволн является первой сравнительной характеристикой, от которых зависит длина вибраторов / габаритов антенны ; и конструкция напрямую предопределяет, какая будет частота электромагнитного колебания приема / передачи … Однако — необязательно длина вибратора антенны должна быть равной длине radiowave : прекрасно работают антенны, где частота electromagnetic oscillation выбрана от &lambda / 2, &lambda / 4 и даже с дробными значениями …

Кроме прямых углов — природа не терпит пустоты … Эта особенность объясняет, почему колебания возмущения среды с переносом энергии не расширяются до бесконечности : сама природа, породившая perturbation with energy transfer — стремится противодействовать ее движениям, стремясь к равновесию и балансу сил, тем активнее, чем выше частота, амплитуда и скорость волнообразных колебаний … Перефразируя размышления Н. Теслы, можно сказать : кто познает природу волны — тот познает природу материи и мироздания …

18:43 31.08.2019

…

Виды волн

Все волны классифицируют по их физической природе, по типу движения частиц материи, по их периодичности и по способу распространения в пространстве.

Согласно типу движения частиц материи при распространении в ней волны выделяют следующие виды:

Поперечные волны — это такой тип возмущения, при котором частицы материи колеблются в направлении, которое перпендикулярно направлению распространения волны. Примером поперечной волны является свет.
Продольные волны — это волны, в которых частицы материи колеблются в направлении распространения волны. Звук является хорошим примером продольной волны.

Согласно физической природе выделяют следующие типы волн:

Механические. Этому типу волн необходимо вещество, чтобы они возникли, то есть твердая, жидкая или газообразная среда. Примером механических волн являются волны на море.
Электромагнитные. Этот тип волн не нуждается в веществе для своего распространения, а может распространяться в вакууме. Ярким примером электромагнитных волн являются радиоволны.
Гравитационные. Эти волны приводят к возмущению пространства-времени. Порождают такие волны крупные космические объекты, например, двойная звезда, которая вращается вокруг общего центра тяжести.

В соответствии с размерностью волны они могут быть:

Одномерные, то есть такие, которые распространяются в одном измерении, например, вибрация веревки.
Двумерные или поверхностные. Эти волны распространяются в двух измерениях, например, волны на поверхности воды.
Трехмерные или сферические. Эти волны распространяются в трех измерениях, например, свет или звук.

В соответствии с периодичностью волны можно сказать, что существуют:

Периодические возмущения, которые отличаются строго повторяющимися характеристиками через определенный промежуток времени, например, звуковые волны.
Не периодические, такие волны не повторяют своих характеристик, через определенные интервалы времени, например, волны электрокардиограммы.

Синусоидальные волны

Согласно теореме Фурье, любая периодическая волна может быть представлена суммой синусоидальных волн различной длины. Эта теорема позволяет изучать каждую периодическую волну благодаря изучению ее синусоидальных компонентов.

Для синусоидальной волны с частотой f, периодом T и скоростью распространения v формула длины волны имеет вид: λ = v/f = v*T.

Скорость распространения волны зависит от типа среды, в которой происходит волновой процесс, а также от частоты колебаний. Скорость распространения электромагнитной волны в вакууме является величиной постоянной и приблизительно равна 3*108 м/с.

Скорость звуковых волн в различных средах

Скорость распространения таких волн определяется характеристиками колебательной среды: ее давлением, температурой и плотностью вещества. Поскольку элементарные частицы, составляющие твердые тела, находятся ближе друг к другу, чем эти частицы в жидкостях, то такая структура твердого вещества позволяет передавать колебательную энергию через него быстрее, чем через жидкость, поэтому скорость распространения волны в них больше. По этой же причине скорость звука в жидкостях выше, чем в газах.

Данные о скорости звука в некоторых средах:

среда	воздух, 20 ºC	вода, 22 ºC	дерево	алюминий	стекло	сталь
скорость, м/с	343	1505	3990	5090	5190	6099

В случае воздуха отметим, что Ньютоном была выведена формула для скорости звука в этой среде в зависимости от температуры, которая впоследствии была модифицирована Лапласом. Эта формула имеет вид: v = 331+0,6*t ºC.

Таким образом, формула для длины звуковой волны с частотой f в воздухе при 25 ºC приобретет вид: λ = v/f = 346/f.

Приведённая комптоновская длина волны

В современной физике чаще употребляется приведённая комптоновская длина волны, которая меньше в 2π раз, то есть выражена не через обычную, а через приведённую постоянную Планка. Приведённая комптоновская длина волны обратна комптоновскому волновому числу:

λ¯C=λC2π=ℏmc.{\displaystyle {\overline {\lambda }}_{C}={\frac {\lambda _{C}}{2\pi }}={\frac {\hbar }{mc}}.}

Для электрона, λeC ≈ 0,00386 Å ≈ 3,8615926764(18)⋅10−13 м; для протона, λpC ≈ 0,0000021 Å ≈ 2,10308910109(97)⋅10−16 м.

В физике ядра и элементарных частиц также имеют важное значение (приведённые) комптоновские длины волн:

пи-мезона: λπC ≈ 1,46⋅10−15 м (характерное расстояние );
W-бозона: λWC ≈ 2,45⋅10−18 м (характерное расстояние слабых взаимодействий).

Приведённая комптоновская длина волны часто возникает в уравнениях квантовой механики и квантовой теории поля. Так, в релятивистском уравнении Клейна — Гордона для свободной частицы

∇2ψ−1c2∂2∂t2ψ=(mcℏ)2ψ{\displaystyle \mathbf {\nabla } ^{2}\psi -{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\psi =\left({\frac {mc}{\hbar }}\right)^{2}\psi }

эта величина (в квадрате) выступает как множитель в правой части. В таком же качестве она появляется и в уравнении Дирака:

iγμ∂μψ=(mcℏ)ψ.{\displaystyle i\gamma ^{\mu }\partial _{\mu }\psi =\left({\frac {mc}{\hbar }}\right)\psi .}

Хотя в традиционное представление уравнения Шрёдингера комптоновская длина волны в явном виде не входит, его можно преобразовать так, чтобы она «проявилась». Так, нестационарное уравнение Шрёдингера для электрона в водородоподобном атоме с зарядовым числом ядра Z

iℏ∂∂tψ=−ℏ22me∇2ψ−14πϵZe2rψ{\displaystyle i\hbar {\frac {\partial }{\partial t}}\psi =-{\frac {\hbar ^{2}}{2m_{e}}}\nabla ^{2}\psi -{\frac {1}{4\pi \epsilon _{0}}}{\frac {Ze^{2}}{r}}\psi }

можно разделить на ℏc{\displaystyle \hbar c} и переписать так, чтобы заменить элементарный заряд e на постоянную тонкой структуры α:

ic∂∂tψ=−12(ℏmec)∇2ψ−αZrψ.{\displaystyle {\frac {i}{c}}{\frac {\partial }{\partial t}}\psi =-{\frac {1}{2}}\left({\frac {\hbar }{m_{e}c}}\right)\nabla ^{2}\psi -{\frac {\alpha Z}{r}}\psi .}

В результате комптоновская длина волны электрона возникает как множитель в первом члене правой части.

В квантовой теории поля часто применяется упрощающая формулы естественная система единиц, в которой скорость света и постоянная Планка равны 1. В такой системе единиц комптоновская длина частицы просто обратна её массе: λ_C = 1/m.