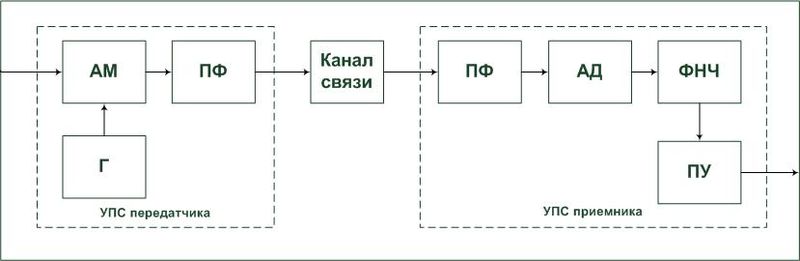
Фазовая модуляция: теория, временная и частотная области
Содержание:
3.3. Сигналы при дискретной модуляции
При дискретной модуляции закодированное сообщение u(t), представляющее собой последовательность кодовых символов {}, преобразовывается в последовательность элементов сигнала {}. Последние отличаются от кодовых символов лишь электрическим представлением. В частном случае дискретная модуляция состоит в воздействии кодовых символов {аi} на переносчик f(t). Такая дискретная модуляция аналогична непрерывной.
Посредством модуляции один из параметров переносчика изменяется по закону, определяемому кодом. При непосредственной передаче переносчиком может быть постоянный ток, изменяющимися параметрами которого являются величина и направление. Обычно же в качестве переносчика, как и при непрерывной модуляции, используется переменный ток (гармоническое колебание). В этом случае можно получить амплитудную (AM), частотную (ЧМ) и фазовую (ФМ) модуляции. Дискретную модуляцию часто называют манипуляцией, а устройство, осуществляющее дискретную модуляцию (дискретный модулятор), называют манипулятором или генератором сигналов.
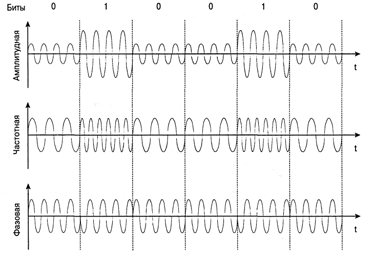
На рис. 3.4 приведены графики сигналов при различных видах манипуляции. При AM символу 1 соответствует передача несущего колебания в течение времени (посылка), символу 0 — отсутствие колебания (пауза). При ЧМ передача несущего колебания с частотой соответствует символу 1, а передача колебания соответствует 0. При ФМ меняется фаза несущей на 180° при каждом переходе от 1 к 0 и от 0 к 1.
Рис. 3.4. Сигналы при различных видах дискретной модуляции
Наконец, в настоящее время применяется относительная фазовая модуляция (ОФМ). В отличие от ФМ, в системе ОФМ фаза несущего колебания изменяется на 180° при передаче символов 1 и остается неизменной при передаче символов 0.
При ОФМ манипуляция каждой данной посылки осуществляется относительно предыдущей. Очевидно, таким способом можно манипулировать (изменять) любой параметр несущего колебания: при изменении частоты получим относительную частотную манипуляцию (ОЧМ), при изменении амплитуды относительную амплитудную манипуляцию (ОАМ). Дельта-модуляция, о которой мы упоминали в § 1.6, также является одним из видов относительной манипуляции.
Рассмотрим спектры сигналов при некоторых видах дискретной модуляции. Будем полагать, что модуляция производится двоичным сообщением u(t), представляющим собой периодическую последовательность прямоугольных импульсов с периодом .
Амплитудная манипуляция. Сигнал AM можно записать в виде
(3.32)
где периодическая функция u(t) на интервале равна:
(3.33)
Представим u(t) рядом Фурье
(3.34)
Тогда сигнал AM запишется в виде
(3.35)
Рис. 3.5. Спектр сигнала при амплитудной манипуляции
Спектр сигнала AM, построенный по ф-лам (3.35), показан на рис. 3.5. Он состоит из несущего колебания с амплитудой и двух боковых полос, спектральные составляющие которых имеют амплитуды
(3.36)
Огибающая спектра дискретного сигнала AM выражается формулой
(3.37)
т. е. представляет собой смещенный на частоту спектр одиночного импульсного сигнала u(t).
Фазовая манипуляция. Сигнал ФМ можно записать в виде
(3.38)
Периодическая функция, определяющая закон изменения фазы на интервале , выражается формулой
(3.39)
Подстановка (3.39) в выражение (3.38) дает
Представим u(t) рядом Фурье
Тогда сигнал ФМ запишется в виде
(3.40)
Рис. 3.6. Спектры сигналов при фазовой манипуляции
Спектр сигнала ФМ для различных значений девиаций фазы , построенной на основании ф-лы (3.40), показан на рис. 3.6. Он состоит из несущего колебания и двух боковых полос. Амплитуда несущего колебания зависит от : и при =— обращается в 0. Амплитуды спектральных составляющих в боковых полосах также зависят от . При увеличении от 0 до , как видно из рис. 3.6, амплитуда несущего колебания убывает до нуля, а амплитуды боковых частот увеличиваются.
Когда =— вся энергия сигнала ФМ содержится только в боковых полосах. Так же, как и при AM, огибающая дискретного спектра боковых частот представляет собой смещенный на частоту спектр одиночного импульсного сигнала u(t), умноженный нa sin:
(3.41)
Аналогично определяется спектр сигнала при частотной манипуляция.
Резюме
- Квадратурная демодуляция может извлекать информацию угла, которая имеет отношение как к частотной модуляции, так и к фазовой модуляции.
- Радиосистемы могут использовать цифровые сигнальные процессоры (в сочетании с аналого-цифровым преобразователем) для применения математического анализа к I/Q сигналам.
- Низкочастотная фаза может быть получена путем вычисления арктангенса отношения Q к I; функция «» необходима, если система должна иметь возможность воспроизведения полных 360° фазы.
- Низкочастотную частоту можно получить, взяв производную от арктангенса отношения Q к I.
Частота против фазы
Частотная и фазовая модуляции тесно связаны; тем не менее, есть ситуации, когда одна из них лучше другой. Различия между ними более выражены при цифровой модуляции.
Аналоговые частотная и фазовая модуляции
Как мы видели в статье про фазовую модуляцию, когда низкочастотный модулирующий сигнал является синусоидой, PM сигнал представляет собой просто сдвинутую версию соответствующего FM сигнала. Поэтому неудивительно, что ни у FM, ни у PM нет никаких серьезных плюсов или минусов, связанных со спектральными характеристиками или восприимчивостью к помехам.
Однако аналоговая частотная модуляция гораздо более распространена, чем аналоговая фазовая модуляция, и причина в том, что схемотехника FM модуляции и демодуляции более проста. Например, частотная модуляция может быть реализована чем-то простым, таким как генератор, построенный с использованием катушки индуктивности и конденсатора, управляемого напряжением (т.е. конденсатора, который изменяет свою емкость в зависимости от напряжения низкочастотного модулирующего сигнала).
Цифровые частотная и фазовая модуляции
Различия между PM и FM становятся весьма значительными, когда мы входим в область цифровой модуляции. При первом рассмотрении – это частота битовых ошибок. Очевидно, что частота битовых ошибок любой системы будет зависеть от разных факторов, но если мы математически сравниваем двоичную PSK систему с эквивалентной двоичной FSK системой, мы обнаружим, что для двоичной FSK требуется передавать значительно больше энергии для достижения той же частоты битовых ошибок. Это является преимуществом цифровой фазовой модуляции.
Но обычная цифровая фазовая модуляция также имеет два существенных недостатка:
- Как обсуждалось в статье про цифровую фазовую модуляцию, обычная (то есть недифференциальная) PSK несовместима с некогерентными приемниками. FSK, напротив, не требует когерентного детектирования.
- Обычные схемы PSK, особенно QPSK, включают в себя резкие изменения фазы, которые приводят к резким изменениям амплитуды модулированного сигнала, а участки с высоким наклоном формы сигнала уменьшаются по амплитуде, когда сигнал обрабатывается фильтром нижних частот. Эти изменения амплитуды в сочетании с нелинейным усилением приводят к проблеме, называемой внеполосным излучением. Чтобы уменьшить внеполосное излучение, мы можем использовать более линейный (и, следовательно, менее эффективный) усилитель мощности или реализовать специализированную версию PSK. Или мы можем перейти на FSK, которая не требует резких изменений фазы.
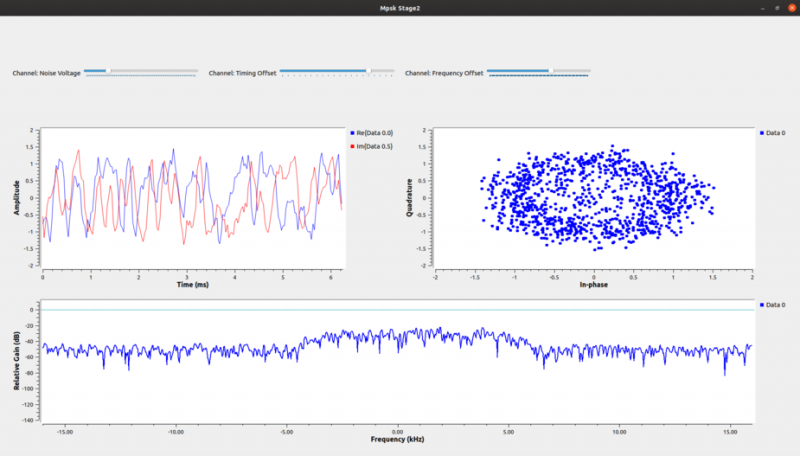
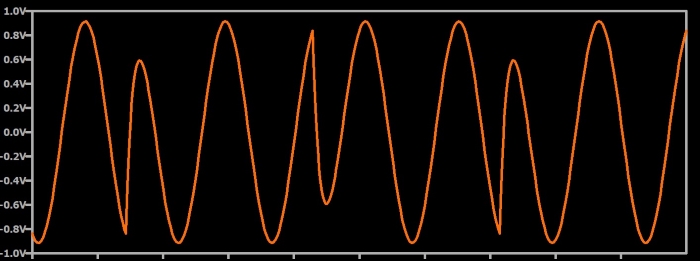Здесь вы можете видеть изменения амплитуды, вызванные фильтрацией нижних частот сигала PSK
Временна́я область
Мы будем использовать те же сигналы, которые использовали при обсуждении FM, то есть несущую 10 МГц и низкочастотный модулирующий сигнал синусоиды 1 МГц:
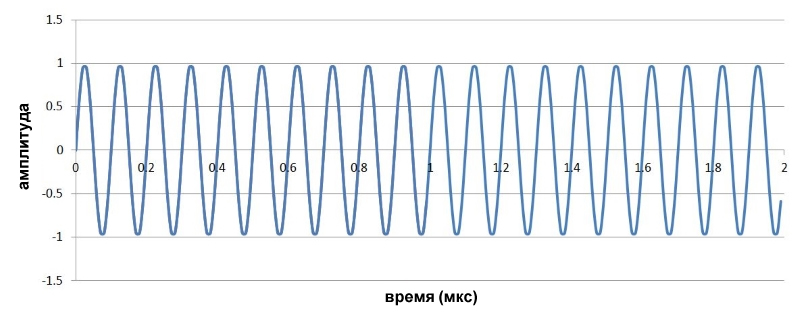Несущая частота
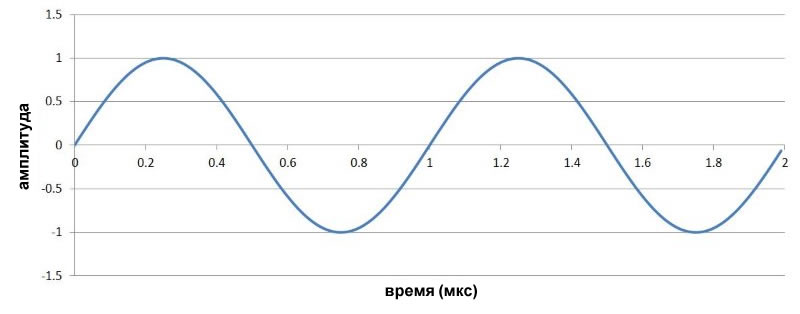Низкочастотный сигнал
Ниже показан частотно-модулированный сигнал (с m=4), который мы видели в предыдущей статье:
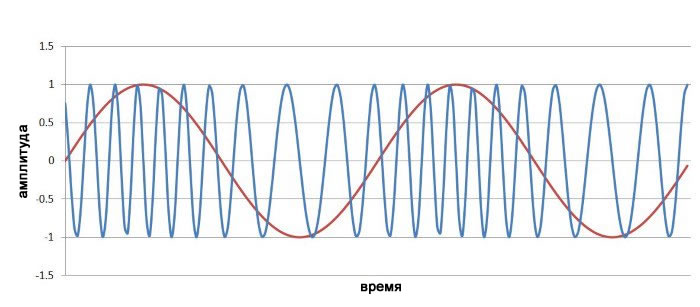Частотная модуляция (m=4)
Мы можем рассчитать форму волны фазомодулированного сигнала, используя следующую формулу, где сигнал, добавленный к аргументу волны сигнала несущей, использует положительный синус (т.е. исходный сигнал) вместо отрицательного косинуса (т.е. интеграла исходного сигнала).
\
Ниже показан график сигнала с фазовой модуляцией:
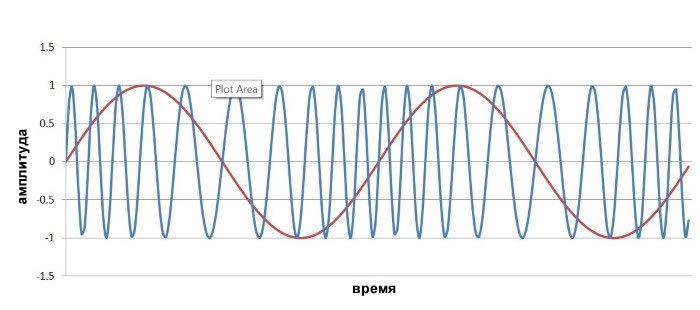Фазовая модуляция (m=4)
Прежде чем обсудить его, давайте посмотрим на диаграмму, которая одновременно показывает формы частотно-модулированного сигнала и фазомодулированного сигнала:
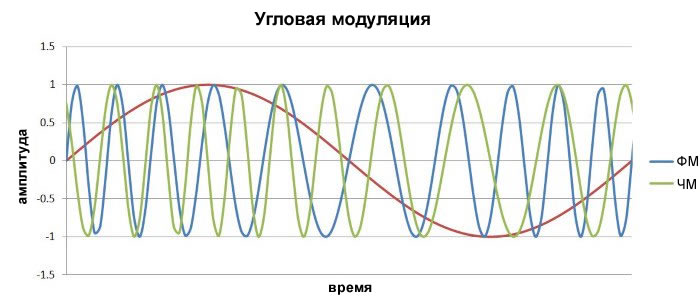Сравнение сигналов с частотной и фазовой модуляциями
Первое, что здесь приходит в голову, это то, что с визуальной точки зрения частотная модуляция более интуитивно понятна по сравнению с фазовой модуляцией; существует четкая визуальная связь между участками с более высокой и низкой частотой и более высокими и более низкими уровнями низкочастотного модулирующего сигнала. В фазовой модуляции связь между низкочастотным модулирующим сигналом и поведением несущей, возможно, не сразу очевидна. Однако после небольшого осмотра мы видим, что частота несущей в фазовой модуляции соответствует наклону формы волны модулирующего сигнала, наиболее высокочастотные участки соответствуют времени самого крутого положительного наклона xнч, а наиболее низкочастотные участки соответствуют времени самого крутого отрицательного наклона.
Это имеет смысл. Напомним, что частота (как функция времени) является производно фазы (как функции времени). При фазовой модуляции наклон формы низкочастотного модулирующего сигнала определяет, как быстро изменяется фаза, и скорость изменения фазы эквивалентна частоте. Поэтому в фазомодулированном сигнале высокий наклон модулирующего сигнала соответствует высокой частоте, а низкий наклон модулирующего сигнала соответствует низкой частоте. В частотной модуляции мы используем интеграл от xнч, который приводит к сдвигу высокочастотных (или низкочастотных) участков несущей к значениям модулирующего сигнала, следующих после высоких (или низких) наклонных участков формы низкочастотного модулирующего сигнала.
Цифровая частотная модуляция
Этот тип модуляции называется частотной манипуляцией (FSK, frequency shift keying). Для наших целей нет необходимости рассматривать математическое выражение частотной манипуляции; скорее мы просто можем указать, что будем иметь частоту f1, когда модулирующие данные равны логическому 0, и частоту f2, когда модулирующие данные равны логической 1.
Временная область
Одним из способов генерации готового для передачи FSK сигнала является сначала создание аналогового низкочастотного сигнала, который переключается между f1 и f2 в соответствии с цифровыми данными. Ниже приведен пример низкочастотного FSK сигнала с f1 = 1 кГц и f2 = 3 кГц. Чтобы гарантировать, что символ имеет одинаковую продолжительность и для логического 0, и для логической 1, мы используем один период для 1 кГц и три периода для 3 кГц.
Аналоговый низкочастотный FSK сигнал
Затем низкочастотный сигнал сдвигается (используя смеситель) до несущей частоты и передается. Этот подход особенно удобен в программных радиосистемах: аналоговый модулирующий сигнал является низкочастотным, и поэтому он может быть сгенерирован математически, а затем введен в аналоговую область с помощью ЦАП. Использование ЦАП для высокочастотного передаваемого сигнала было бы намного сложнее.
Более простой способ реализации FSK состоит в том, чтобы просто иметь два сигнала несущей с разными частотами (f1 и f2); и тот или иной сигнал подается на выход в зависимости от логического уровня двоичных данных. Это приводит к конечному передаваемому сигналу, который резко переключается между двумя частотами, так же, как низкочастотный FSK сигнал, за исключением того, что разница между двумя частотами здесь намного меньше по сравнению со средней частотой. Другими словами, если бы вы смотрели на график во временной области, было бы сложно визуально различить участки с f1 от участков с f2, потому что разница между f1 и f2 является лишь крошечной долей f1 (или f2).
Частотная область
Давайте посмотрим на результат частотной манипуляции в частотной области. В этом случае мы будем использовать ту же несущую частоту 10 МГц (или, в этом случае, среднюю частоту), и будем использовать ±1 МГц в качестве отклонения (это не реальный пример, но удобный для наших целей). Таким образом, передаваемый сигнал будет 9 МГц для логического 0 и 11 МГц для логической 1. Ниже показан спектр полученного сигнала:
Спектр сигнала с частотной манипуляцией
Обратите внимание, что на «несущей частоте» нет энергии. Это неудивительно, учитывая, что модулированный сигнал никогда не находится на частоте 10 МГц
Он всегда находится на частоте 10 МГц минус 1 МГц или 10 МГц плюс 1 МГц, и именно там мы видим два доминирующих всплеска: 9 МГц и 11 МГц.
Но что насчет других частот, присутствующих в этом спектре? Ну, спектральный анализ FSK не особенно прост. Мы знаем, что будет добавлена дополнительная энергия Фурье, связанная с резкими переходами между частотами. Оказывается, что FSK приводит к sinc-функциональному типу спектра для каждой частоты, то есть один центрирован на f1, а другой центрирован на f2. Они учитывают дополнительные частотные всплески по обе стороны от двух доминирующих пиков.
Цифровая модуляция (манипуляция)[править]
Тот самый вид модуляции, который используется для передачи данных в компьютерных сетях.
| Определение: |
| Цифровой модуляцией называется процесс преобразования битов в соответствующие аналоговые сигналы. |
Цифровую модуляцию принято называть манипуляцией, поэтому часто может встречаться именно этот термин.
Носителем так же, как и в случае аналоговой модуляции является колебание.
Основные методы цифровой модуляцииправить
- Амплитудная
- Частотная
- Фазовая
- Квадратурная амплитудная (амплитудно-фазовая)
| Амплитудная (ASK — Amplitude Shift Keying) | Частотная (FSK — Frequency Shift Keying) | Фазовая (PSK — Phase Shift Keying) | Квадратурная амплитудная (QAM — Quadrature Amplitude Modulation) |
|---|---|---|---|
| Меняется амплитуда импульсов | Меняется частота импульсов | Меняется фаза колебания | Меняется одновременно и амплитуда, и фаза |
| Для передачи 1 используется большая амплитуда, для передачи 0 — малая, иногда нулю соответствует отсутствие колебания. | Для передачи 1 используется высокая частота колебаний, для передачи 0 — низкая. | Для передачи 1 используется сдвиг фазы на . | Для передачи 1 используется большая амплитуда и сдвиг фазы на . |
Многопозиционные методыправить
Для разных видов манипуляции существуют методы, позволяющие передавать не только 0 и 1 в рамках одного сигнала, такие методы получили название многопозиционные.
Суть этих методов в том, что один элемент линейного сигнала несет информацию о большем числе битов, чем в обычных двухпозиционных методах.
Работает это очень просто. Например, в многопозиционной амплитудной манипуляции зададим не 2 амплитуды, которые будут кодировать 0 или 1, а 4, которые будут соответствовать 00, 01, 10, 11 по мере увеличения амплитуды. Для многопозиционной частотной манипуляции используется больше частот, а для многопозиционной фазовой манипуляции, соответственно, больше сдвигов.
Да, это действительно позволяет повысить удельную скорость передачи информации, но при этом начинают возникать ошибки, связанные с погрешностью передачи.
Рассмотрим самые распространенные методы:
BPSK, QPSK, 8-PSKправить
| BPSK | QPSK | 8-PSK |
|---|---|---|
| Binary Phase Shift Keying является обычной бинарной фазовой манипуляцией, которую мы рассматривали выше в рамках основных методов, позволяет закодировать 1 бит информации за сигнал. Не является многопозиционным методом. | Quadrature Phase Shift Keying переводится как квадратурная фазовая манипуляция и представляет собой разделение на 4 фазы, которые позволяют закодировать 2 бита за сигнал. | 8 Phase Shift Keying представляет собой разделение на 8 фаз, которые позволяют закодировать 3 бита за сигнал. |
QAM-16, QAM-64править
С простой квадратурной амплитудной манипуляцией мы уже знакомы, теперь посмотрим на 2 многопозиционные вариации. Напомню, что это комбинация амплитудной и фазовой манипуляций.
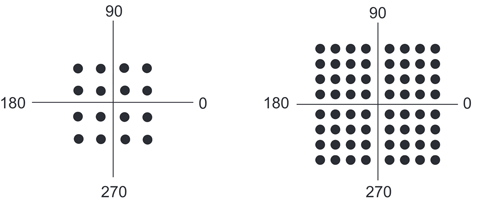
QAM-16 использует 16 комбинаций амплитудных и фазовых сдвигов, которые позволяют передавать 4 бита информации за 1 сигнал, а с помощью QAM-64, который использует 64 комбинации, можно передать целых 6 бит за сигнал.
Каждая комбинация задается углом, который соответствует фазе и расстоянием от начала координат, которое показывает величину амплитуды.
Ниже показана симуляция принципа работы квадратурной амплитудной манипуляции на примере QAM-16 и расположение точек для QAM-16 и QAM-64 соответственно.
Свойства
Свойства аналоговых сигналов в значительной мере являются противоположностью свойств квантованных или цифровых сигналов.
Отсутствие чётко отличимых друг от друга дискретных уровней сигнала приводит к невозможности применить для его описания понятие информации в том виде, как она понимается в цифровых технологиях. Содержащееся в одном отсчёте «количество информации» будет ограничено лишь динамическим диапазоном средства измерения.
Отсутствие избыточности. Из непрерывности пространства значений следует, что любая помеха, внесённая в сигнал, неотличима от самого сигнала и, следовательно, исходная амплитуда не может быть восстановлена. В действительности фильтрация возможна, например, частотными методами, если известна какая-либо дополнительная информация о свойствах этого сигнала (в частности, полоса частот).
Импульсные методы модуляции
Импульсная модуляция — изменение параметров импульсных сигналов во времени или в пространстве. Обычно импульсная модуляция представляет собой разновидность модулированных колебаний, где в качестве «переносчика» информации используется последовательность импульсов. Вид импульсной модуляции определяется законом изменения параметров (амплитуды, длительности, фазы, частоты следования) импульсных сигналов.
Сущность импульсных методов модуляции
Переносчиком информации является периодическая последовательность импульсов. Она характеризуется такими параметрами, как амплитуда, длительность (ширина) импульса, частота следования импульсов, положение (фаза) каждого импульса на оси времени по отношению к так называемым тактовым точкам. Соответственно различают амплитудно-импульсную (АИМ), широтно-импульсную (ШИМ), частотно-импульсную (ЧИМ) и фазово-импульсную (ФИМ) модуляцию. В ряде случаев непрерывные сигналы квантуются по времени и уровню. Полученные при этом дискретные значения преобразуют в кодовые комбинации, состоящие из импульсов равной амплитуды и длительности, (по существу, в цифровую форму), обеспечивая кодово-импульсную модуляцию (КИМ или ИКМ). Видеоимпульсами КИМ может осуществляться амплитудная, частотная, фазовая и другая модуляция несущего колебания.
Различные виды импульсной модуляции: а — немодулированная последовательность импульсов; б — модулирующий (информационный) сигнал; в — амплитудно-импульсная модуляция; г — широтно-импульсная модуляция; д — частотно-импульсная модуляция; г — фазово-импульсная модуляция.
В системах оптической и высокочастотной радиолокации и связи импульсную модуляцию применяют для модуляции гармонических сигналов (см. АМ (Амплитудная модуляция) ). В этом случае возможна реализация сложных видов импульсных модуляций, когда наряду с изменением параметров огибающей (последовательности импульсов) используется модуляция высокочастотного заполнения импульсов. Примером такой импульсной модуляции может служить линейно-частотная модуляция, реализующая изменение частоты заполнения по линейному закону.
Линейно-частотная модуляция: а-форма сигнала; б -закон изменения частоты заполнения (w0 — несущая частота; wд- девиация частоты).
В радиолокации импульсная модуляция позволяет не только сформировать мощные кратковременные излучения для обнаружения и определения параметров движения целей, но и получить конкретные оценки их размеров, конфигурации, скорости вращения вокруг центра тяжести. Импульсную модуляцию используют также для идентификации физических параметров (температуры, плотности, степени ионизации и т. д.) различных объектов и сред.
Демодуляция модулированных импульсных сигналов
Это процесс выделения полезной составляющей из спектра принимаемых сигналов.
При АИМ она может быть выделена фильтром нижних частот (ФНЧ). Полоса пропускания ФНЧ рассчитывается на неискаженное выделение сигнала с максимальной шириной спектра 2Fmax{\displaystyle F_{n}>2F_{max}\,\!}
При большой скважности импульсов, когда амплитуда напряжения модулирующих частот становится мала, перед фильтром ставят пиковый детектор, напряжение на выходе которого приближается к огибающей модулированных импульсов.
При ШИМ основным методом выделения полезной составляющей является демодуляция с помощью фильтра низких частот. Поскольку тактовые частоты окружены бесконечным количеством пар боковых частот, в полосу пропускания фильтра попадают частотные составляющие mFu−nF(m,n=,1,2,…){\displaystyle mF_{u}-nF(m,n=0,1,2,…)\,\!}, вызывающие искажения передаваемого сигнала. Считают, что неискаженный прием обеспечивается, если FuFmax>3…6{\displaystyle F_{u}/F_{max}>3…6\,\!}.
При ФИМ амплитуда полезной составляющей мала и зависит от частоты. Перед модуляцией ФИМ преобразуют поэтому в ШИМ или в АИМ.
При использовании КИМ в телефонии преобразователи цифра—аналог преобразуют КИМ последовательно в АИМ и в непрерывный сигнал.
Математика
В первой статье данной главы мы обсудили парадоксальную величину, называемую мгновенной частотой. Если вы считаете этот термин незнакомым или запутанным, вернитесь на эту страницу и прочитайте раздел «Частотная модуляция (ЧМ, англ. FM) и фазовая модуляция (ФМ, англ. PM)». Тем не менее, вы всё еще можете быть немного запутаны, и это понятно: идея мгновенной частоты нарушает основной принцип, согласно которому «частота» указывает, как часто сигнал завершает полный цикл: десять раз в секунду, миллион раз в секунду или сколько бы то ни было раз.
Мы не будем пытаться заниматься каким-либо тщательным или всесторонним рассмотрением мгновенной частоты в качестве математической концепции
(Если вы намерены подробно изучить эту проблему, вот академический документ, который должен помочь.) В контексте FM важно понять, что мгновенная частота естественно вытекает из того, что частота сигнала несущей изменяется непрерывно в ответ на модулирующую волну (т.е. низкочастотный сигнал)
Мгновенное значение модулирующего сигнала влияет на частоту в определенный момент, а не на частоту одного или нескольких полных циклов.
На самом деле это верно только для аналоговой частотной модуляции; в цифровой ЧМ один бит соответствует дискретному числу циклов. Это приводит к интересной ситуации, когда более старая технология (аналоговая ЧМ) менее интуитивно понятна, чем более новая технология (цифровая частотная модуляция, также называемая частотной манипуляцией или FSK (Frequency Shift Keying)).
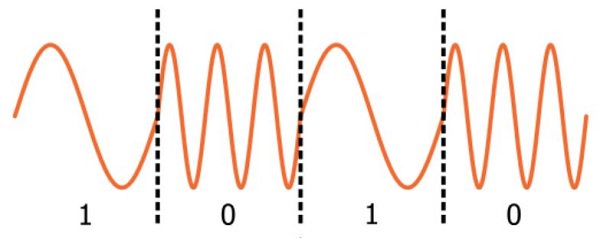Вам не нужно размышлять над мгновенной частотой, чтобы понимать цифровую частотную модуляцию
Как и в предыдущей статье мы будем обозначать несущую как sin(ωнесt). У нее уже есть частота (а именно, ωнес), поэтому мы должны использовать термин «дополнительное отклонение частоты» для обозначения частотной составляющей, внесенной процедурой модуляции. Этот термин несколько вводит в заблуждение, поскольку «дополнительное» подразумевает более высокую частоту, тогда как модуляция может приводить к несущей частоте, которая выше или ниже номинальной несущей частоты. Фактически поэтому частотная модуляция (в отличие от амплитудной модуляции) не требует смещенного низкочастотного сигнала: положительные значения низкочастотного сигнала увеличивают частоту несущей, а отрицательные значения низкочастотного сигнала уменьшают частоту несущей. В этих условиях демодуляция не является проблемой, поскольку все значения низкочастотного сигнала соответствуют уникальным частотам.
В любом случае, вернемся к нашему сигналу несущей: sin(ωнесt). Если мы добавим низкочастотный сигнал (xнч) к величине внутри круглых скобок, мы получим отклонение фазы, линейно пропорциональное низкочастотному сигналу. Но нам нужна частотная модуляция, а не фазовая, поэтому мы хотим, чтобы линейно пропорционально низкочастотному сигналу было отклонение частоты. Из первой статьи данной главы мы знаем, что мы можем получить частоту, взяв производную фазы по времени. Таким образом, если мы хотим, чтобы частота была пропорциональна xнч, мы должны добавить не сам низкочастотный сигнал, а скорее интеграл от низкочастотного сигнала (поскольку взятие производной отменяет интеграл, у нас остается xнч как отклонение частоты).
\
Единственное, что нам нужно здесь добавить, это индекс модуляции m. В предыдущей статье мы увидели, что индекс модуляции можно использовать для того, чтобы изменения амплитуды несущей были более или менее чувствительны к изменениям амплитуды низкочастотного сигнала. Его функция в FM аналогична: индекс модуляции позволяет нам точно настраивать интенсивность изменения частоты, которое возникает при изменении амплитуды низкочастотного сигнала.
\
Амплитудная модуляция
Амплитудная модуляция проста в плане реализации и анализа. Кроме того, AM сигналы довольно легко демодулировать. В целом, тогда AM можно рассматривать как простую, недорогую схему модуляции. Однако, как обычно, простота и низкая стоимость сопровождаются компромиссами в производительности – мы никогда не ожидаем, что более простое и дешевое решение будет самым лучшим.
Возможно, я буду неточным, если опишу AM системы как «редкие», поскольку AM приемники присутствуют на бесчисленных транспортных средствах. Однако применения аналоговой амплитудной модуляции в настоящее время весьма ограничены, поскольку AM имеет два существенных недостатка.
Помимо AM радиовещания, аналоговая амплитудная модуляция используется в гражданской авиации
Амплитудный шум
Шум – это постоянная проблема в беспроводных системах связи. В определенном смысле качество радиочастотного проекта можно суммировать по отношению сигнал/шум демодулированного сигнала: меньше шума в принятом сигнале означает более высокое качество (для аналоговых систем) или меньшее количество битовых ошибок (для цифровых систем). Шум присутствует всегда, и мы всегда должны признавать в нем основную угрозу для производительности системы.
Шум – случайный электрический шум, помехи, электрические и механические переходные процессы – воздействует на уровень сигнала. Другими словами, шум может создавать амплитудную модуляцию. И это является проблемой, поскольку случайную амплитудную модуляцию, возникающую из-за шума, нельзя отличить от преднамеренной амплитудной модуляции, выполняемой передатчиком. Шум является проблемой для любого радиосигнала, но AM системы особенно восприимчивы.
Линейность усилителя
Одной из основных проблем в разработке радиочастотных усилителей мощности является линейность (более конкретно, трудно добиться и высокой эффективности, и высокой линейности одновременно). Линейный усилитель применяет к входному сигналу определенный фиксированный коэффициент усиления; графически это выглядит так: передаточная функция линейного усилителя представляет собой просто прямую линию с наклоном, соответствующим коэффициенту усиления.
Прямая линия представляет собой отклик идеального линейного усилителя: выходное напряжение всегда равно входному напряжению, умноженному на фиксированный коэффициент усиления
У реальных усилителей всегда есть некоторая степень нелинейности, что означает, что на усиление, применяемое к входному сигналу, влияют характеристики входного сигнала. Результатом нелинейного усиления являются искажения, т.е. создание энергии на частотах гармоник.
Можно также сказать, что нелинейное усиление является формой амплитудной модуляции. Если коэффициент усиления усилителя изменяется в зависимости от частоты входного сигнала или в соответствии с внешними факторами, такими как температура или состояние источника питания, передаваемый сигнал будет испытывать непреднамеренную (и нежелательную) амплитудную модуляцию. Это является проблемой в AM системах, поскольку паразитная амплитудная модуляция мешает преднамеренной амплитудной модуляции.
Любая схема модуляции, которая включает в себя изменения амплитуды, более восприимчива к влиянию нелинейности. Это включает в себя как обычную аналоговую амплитудную модуляцию, так и широко используемые цифровые схемы, известные в совокупности как квадратурная амплитудная модуляция (QAM).
4.2. Сигналы с непрерывной амплитудной модуляцией
Рассмотрение модулированных сигналов начнем с сигналов, у которых в качестве изменяемого параметра выступает амплитуда несущего колебания. Модулированный сигнал в этом случае является амплитудно-модулированным или сигналом с амплитудной модуляцией (АМ-сигналом).
Как уже было отмечено выше, основное внимание будет уделено сигналам, несущее колебание которых представляет собой гармоническое колебание вида
,
где – амплитуда несущего колебания,
– частота несущего колебания.
Здесь и далее полагается, что начальные фазы гармонических колебаний равны нулю.
В качестве модулирующих сигналов сначала рассмотрим непрерывные сигналы . Тогда модулированные сигналы будут являться сигналами с непрерывной амплитудной модуляцией. Такой сигнал описывается выражением
, (4.2)
где – огибающая АМ-сигнала,
– коэффициент амплитудной модуляции.
Из выражения (4.2) следует, что АМ-сигнал представляет собой произведение огибающей на гармоническую функцию . Коэффициент амплитудной модуляции характеризует глубину модуляции и в общем случае описывается выражением
. (4.3)
Очевидно, при сигнал представляет собой просто несущее колебание.
Для более детального анализа характеристик АМ-сигналов рассмотрим простейший АМ-сигнал, в котором в качестве модулирующего сигнала выступает гармоническое колебание
, (4.4)
где , – соответственно амплитуда и частота модулирующего (управляющего) сигнала, причем . В этом случае сигнал описывается выражением
, (4.5)
и называется сигналом однотональной амплитудной модуляции.
На рис. 4.2 изображены модулирующий сигнал , колебание несущей частоты и сигнал .
Для такого сигнала коэффициент глубины амплитудной модуляции равен
.
Воспользовавшись известным тригонометрическим соотношением
после несложных преобразований получим
(4.6)
Выражение (4.6) устанавливает спектральный состав однотонального АМ-сигнала. Первое слагаемое представляет собой немодулированное колебание (несущее колебание). Второе и третье слагаемые соответствуют новым гармоническим составляющим, появившимся в результате модуляции амплитуды несущего колебания; частоты этих колебаний и называются нижней и верхней боковыми частотами, а сами составляющие – нижней и верхней боковыми составляющими.
Амплитуды этих двух колебаний одинаковы и составляют величину
, ( 4.7)
На рис. 4.3 изображен амплитудный спектр однотонального АМ-сигнала. Из этого рисунка следует, что амплитуды боковых составляющих располагаются симметрично относительно амплитуды и начальной фазы несущего колебания. Очевидно, ширина спектра однотонального АМ-сигнала равна удвоенной частоте управляющего сигнала
.
В общем случае, когда управляющий сигнал характеризуется произвольным спектром, сосредоточенным в полосе частот от до , спектральный характер АМ-сигнала принципиально не отличается от однотонального.
На рис. 4.4 изображены спектры управляющего сигнала и сигнала с амплитудной модуляцией. В отличие от однотонального АМ-сигнала в спектре произвольного АМ-сигнала фигурируют нижняя и верхняя боковые полосы. При этом верхняя боковая полоса является копией спектра управляющего сигнала, сдвинутой по оси частот на
величину , а нижняя боковая полоса представляет собой зекальное отображение верхней. Очевидно, ширина спектра произвольного АМ-сигнала
, (4.8)
т.е. равна удвоенной верхней граничной частоте управляющего сигнала.
Возвратимся к сигналу однотональной амплитудной модуляции и найдем его энергетические характеристики. Средняя мощность АМ-сигнала за период управляющего сигнала определяется по формуле:
. (4.9)
Так как , а , положим , где . Подставляя выражение (4.6) в (4.9), после несложных, но достаточно громоздких преобразований с учетом того, что и с использованием тригонометрических соотношений
и ,
получим
. (4.10)
Здесь первое слагаемое характеризует среднюю мощность несущего колебания, а второе – суммарную среднюю мощность боковых составляющих, т.е.
.
Так как суммарная средняя мощность боковых составляющих делится поровну между нижней и верхней, что вытекает из (4.7), то отсюда следует
. (4.11)
Таким образом, на передачу несущего колебания в АМ-сигнале тратится более половины мощности (с учетом того, что ), чем на передачу боковых составляющих. Так как информация заложена именно в боковых составляющих, передача составляющей несущего колебания нецелесообразна с энергетической точки зрения. Поиск более эффективных методов использования принципа амплитудной модуляции приводит к сигналам балансной и однополосной амплитудной модуляции.
