Дифференцирующая rc-цепь и ее характеристики
Содержание:
- Процесс заряда конденсатора
- Интегрирующая цепь RC
- 2.1. Квазистационарные процессы. RC- и RL-цепи
- Коррекция коэффициента мощности
- Навигация¶
- Фазовая цепь RC
- Порядок выполнение работы
- Навигация¶
- Особые режимы работы цепи
- Теоретическое обоснование¶
- Экспериментальное измерение импеданса
- Дифференцирующая RC-цепь.
- Дифференцирующая RC-цепь
Процесс заряда конденсатора
На схеме представлена RC – цепь (интегрирующая), запитанная от постоянного источника питания. При замыкании ключа в положение 1 происходит заряд конденсатора. Ток проходит по цепи: “плюс
” источника – резистор – конденсатор — “минус” источника.
Напряжение на обкладках конденсатора изменяется по экспоненциальному закону. Ток, протекающий через конденсатор, также изменяется по экспоненте. Причем эти изменения взаимообратны, чем больше напряжение, тем меньше ток, протекающий через конденсатор. Когда напряжение на конденсаторе сравняется с напряжением источника, процесс заряда прекратится, и ток в цепи перестанет течь.
Теперь, если мы переключим ключ в положение 2, то ток потечет в обратную сторону, а именно по цепи: конденсатор – резистор – “минус” источника. Таким образом, конденсатор разрядится. Процесс будет носить также экспоненциальный характер.
Важной характеристикой данной цепи является произведение RC
, которую еще называют постоянной времени
τ. За время τ конденсатор заряжается или разряжается на 63%
За 5 τ конденсатор отдает или принимает заряд полностью.
От теории перейдем к практике. Возьмем конденсатор на 0,47 мкФ и резистор номиналом 10 КОм.
Рассчитаем примерное время, за которое должен зарядиться конденсатор.
Теперь соберем данную схему в multisim и попробуем промоделировать
Собранная схема, запитана от батареи 12 В. Меняя положение переключателя S1, мы сначала заряжаем, а затем разряжаем конденсатор через сопротивление R = 10 КОм. Для того чтобы увидеть наглядно работу схемы посмотрите видео ниже.
Конденсатор – элемент, способный накапливать электрическую энергию.
Название происходит от латинского слова «condensare» — «сгущать», «уплотнять».
Первый конденсатор был создан в 1745 году Питером ванн Мушенбруком. В честь города Лейдена, в котором его создали, изобретение впоследствии назвали «Лейденской банкой».
Конденсатор состоит из металлических электродов – обкладок, между которыми находится диэлектрик. По сравнению с обкладками, диэлектрик имеет небольшую толщину. Это и определяет свойство конденсатора накапливать заряд: положительные и отрицательные заряды на его обкладках удерживают друг друга, взаимодействуя через тонкий непроводящий слой.
Емкость конденсатора
зависит от:
- площади обкладок (S);
- расстояния между ними (d);
- диэлектрической проницаемости материала диэлектрика между обкладками (ԑ).
Связаны они между собой формулой (формула емкости конденсатора):
Для увеличения площади обкладок пластины некоторых конденсаторов изготавливают из полосок фольги, разделенных полоской диэлектрика и скрученных в рулон. Увеличить емкость также можно уменьшением толщины диэлектрика между обкладками и применением материалов с большей диэлектрической проницаемостью. Между обкладками конденсаторов располагают твердые, жидкие вещества и газы, в том числе и воздух.
Конденсаторы небольшой емкости получают на печатных платах, располагая две дорожки напротив друг друга.
Каким бы качественным не был диэлектрик в конденсаторе, он все равно имеет сопротивление. Его величина велика, но в заряженном состоянии конденсатора ток между обкладками все равно есть. Это приводит к явлению «саморазряда
»: заряженный конденсатор со временем теряет свой заряд.
Интегрирующая цепь RC
Рассмотрим электрическую цепь из резистора сопротивлением R и конденсатора ёмкостью C,
представленную на рисунке.
Элементы R и C соединены последовательно,
значит, ток в их цепи можно выразить, исходя из производной напряжения заряда конденсатора dQ/dt = C(dU/dt) и закона Ома U/R.
Напряжение на выводах резистора обозначим UR.
Тогда будет иметь место равенство:
Проинтегрируем последнее выражение . Интеграл левой части уравнения будет равен Uout + Const .
Перенесём постоянную составляющую Const в правую часть с тем же знаком. В правой части постоянную времени RC
вынесем за знак интеграла:
В итоге получилось, что выходное напряжение Uout прямо-пропорционально интегралу напряжения на выводах резистора,
следовательно, и входному току Iin.
Постоянная составляющая Const не зависит от номиналов элементов цепи.
Чтобы обеспечить прямую пропорциональную зависимость выходного напряжения Uout от интеграла входного Uin,
необходима пропорциональность входного напряжения от входного тока.
Нелинейное соотношение Uin/Iin во входной цепи вызвано тем,
что заряд и разряд конденсатора происходит по экспоненте e-t/τ, которая наиболее нелинейна при t/τ ≥ 1,
то есть, когда значение t соизмеримо или больше τ.
Здесь t — время заряда или разряда конденсатора в пределах периода.τ = RC — постоянная времени — произведение величин R и C.
Если взять номиналы RC цепи, когда τ будет значительно больше t,
тогда начальный участок экспоненты для короткого периода (относительно τ) может быть достаточно линейным,
что обеспечит необходимую пропорциональность между входным напряжением и током.
Для простой цепи RC постоянную времени обычно берут на 1-2 порядка больше периода переменного входного сигнала,
тогда основная и значительная часть входного напряжения будет падать на выводах резистора, обеспечивая в достаточной степени линейную зависимость
Uin/Iin ≈ R.
В таком случае выходное напряжение Uout будет с допустимой погрешностью пропорционально интегралу входного Uin.
Чем больше величины номиналов RC, тем меньше переменная составляющая на выходе, тем более точной будет кривая функции.
В большинстве случаев, переменная составляющая интеграла не требуется при использовании таких цепей, нужна только постоянная Const,
тогда номиналы RC можно выбирать по возможности большими, но с учётом входного сопротивления следующего каскада.
В качестве примера, сигнал с генератора — положительный меандр 1V периодом 2 mS подадим на вход простой интегрирующей цепи RC с номиналами:R = 10 kOhm, С = 1 uF. Тогда τ = RC = 10 mS.
В данном случае постоянная времени лишь в пять раз больше времени периода, но визуально интегрирование прослеживается в достаточной степени точно.
График показывает, что выходное напряжение на уровне постоянной составляющей 0.5в будет треугольной формы, потому как участки,
не меняющиеся во времени, для интеграла будут константой (обозначим её a), а интеграл константы будет линейной функцией.
∫adx = ax + Const. Величина константы a определит тангенса угла наклона линейной функции.
Проинтегрируем синусоиду, получим косинус с обратным знаком ∫sinxdx = -cosx + Const.
В данном случае постоянная составляющая Const = 0.
Если подать на вход сигнал треугольной формы, на выходе будет синусоидальное напряжение.
Интеграл линейного участка функции — парабола. В простейшем варианте ∫xdx = x2/2 + Const.
Знак множителя определит направление параболы.
Недостаток простейшей цепочки в том, что переменная составляющая на выходе получается очень маленькой относительно входного напряжения.
Рассмотрим в качестве интегратора Операционный Усилитель (ОУ) по схеме, показанной на рисунке.
С учётом бесконечно большого сопротивления ОУ и правила Кирхгофа здесь будет справедливо равенство:
Iin = IR = Uin/R = — IC.
Напряжение на входах идеального ОУ здесь равно нулю, тогда на выводах конденсатора
UC = Uout = — Uin .
Следовательно, Uout определится, исходя из тока общей цепи.
При номиналах элементов RC, когда τ = 1 Sec,
выходное переменное напряжение будет равно по значению интегралу входного. Но, противоположно по знаку.
Идеальный интегратор-инвертор при идеальных элементах схемы.
2.1. Квазистационарные процессы. RC- и RL-цепи
В цепях постоянного тока распределение электрических зарядов на проводниках и токов на участках цепи стационарно, то есть неизменно во времени. Электромагнитное поле в таких цепях состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Эти поля существуют независимо друг от друга.
Если на каком-то участке цепи происходят изменения силы тока или напряжения, то другие участки цепи могут «почувствовать» эти изменения только через некоторое время, которое по порядку величины равно времени τ распространения электромагнитного возмущения от одной точки цепи к другой. Так как электромагнитные возмущения распространяются с конечной скоростью, равной скорости света c , то где l – расстояние между наиболее удаленными точками цепи. Если это время τ много меньше длительности процессов, происходящих в цепи, то можно считать, что в каждый момент времени сила тока одинакова во всех последовательно соединенных участках цепи. Процессы такого рода в электрических цепях а также сами цепи, называются квазистационарными.
Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи.
Из-за огромного значения скорости света время установления в цепи электрического равновесия оказывается весьма малым. Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные.
Простыми примерами квазистационарных процессов могут служить процессы, происходящие в RC- и RL-цепях при подключении и отключении источника постоянного тока.
На рис. 2.1.1 изображена электрическая цепь, состоящая из конденсатора с емкостью C, резистора с сопротивлением R и источника тока с ЭДС, равной .
| Рисунок 2.1.1.Цепи зарядки и разрядки конденсатора через резистор |
Если замкнуть ключ K в положение 1, то начинается процесс зарядки конденсатора через резистор. Для квазистационарной цепи по закону Ома можно записать:
JUJqUq / C
Мы получили дифференциальное уравнение, описывающее процесс зарядки конденсатора. Если конденсатор вначале не был заряжен, то решение этого уравнения имеет вид
τ = RCпостоянная времениt → ∞U (t) →
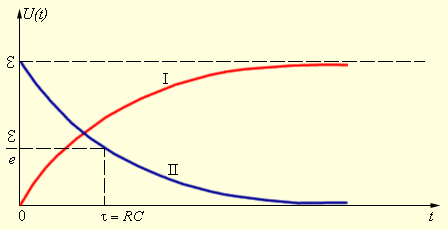 |
| Рисунок 2.1.2.Зарядка (I) и разрядка (II) конденсатора через резистор |
Если после того, как конденсатор полностью зарядился до напряжения , ключ K перебросить в положение 2, то начнется процесс разрядки. Внешний источник тока в цепи разрядки отсутствует ( = 0). Процесс разрядки описывается выражением
Зависимость U (t) в процессе разрядки изображена на рис. 2.1.2 (II). При t = τ напряжение на конденсаторе уменьшается в e ≈ 2,7 раз.
Аналогично протекают процессы в цепи, содержащей катушку с индуктивностью L и резистор с сопротивлением R (рис. 2.1.3).
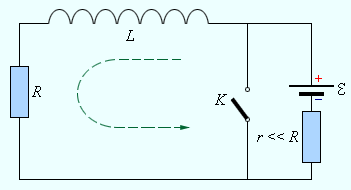 |
| Рисунок 2.1.3.Цепь, содержащая катушку с индуктивностью L, резистор с сопротивлением R и источник тока с ЭДС, равной |
Если в цепи, изображенной на рис. 2.1.3, ключ K сначала был замкнут, а затем внезапно разомкнут, то начнется процесс установления тока
Следует обратить внимание на то, что в схему последовательно с источником тока включен резистор r с малым сопротивлением, чтобы при замкнутом ключе K батарея не оказалась закороченной. Поскольку r
Этот процесс описывается уравнением
Это уравнение по виду совпадает с уравнением, описывающим зарядку конденсатора, только теперь переменной величиной является сила тока J. Решение этого уравнения имеет вид
τ = L / RRLK
Следует отметить, что процессы в RC- и RL-цепях аналогичны механическим процессам при движении тела в вязкой жидкости.
 |
|
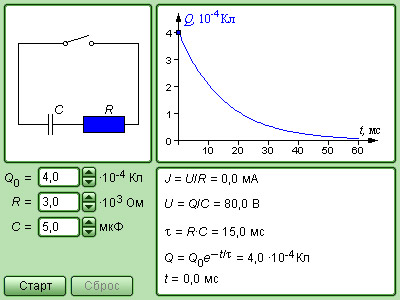
Модель. RC-контур |
 |
|
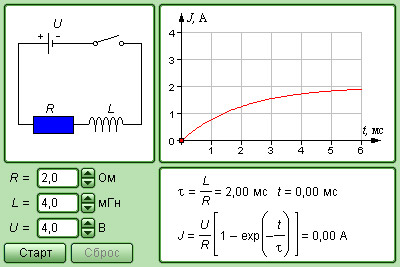
Модель. RL-контур |
Коррекция коэффициента мощности
Коррекция коэффициента мощности при помощи конденсаторов
Коррекция коэффициента мощности (англ. power factor correction (PFC)) — процесс приведения потребления конечного устройства, обладающего низким коэффициентом мощности при питании от силовой сети переменного тока, к состоянию, при котором коэффициент мощности соответствует принятым стандартам.
К ухудшению коэффициента мощности (изменению потребляемого тока непропорционально приложенному напряжению) приводят нерезистивные нагрузки: реактивная и нелинейная. Реактивные нагрузки корректируются внешними реактивностями, именно для них определена величина cosφ{\displaystyle \cos \varphi }. Коррекция нелинейной нагрузки технически реализуется в виде той или иной дополнительной схемы на входе устройства.
Данная процедура необходима для равномерного использования мощности фазы и исключения перегрузки нейтрального провода трёхфазной сети. Так, она обязательна для импульсных источников питания мощностью в 100 и более ватт[источник не указан 3367 дней]. Компенсация обеспечивает отсутствие всплесков тока потребления на вершине синусоиды питающего напряжения и равномерную нагрузку на силовую линию.
Разновидности коррекции коэффициента мощности
- Коррекция реактивной составляющей полной мощности потребления устройства. Выполняется путём включения в цепь реактивного элемента, производящего обратное действие. Например, для компенсации действия электродвигателя переменного тока, обладающего высокой индуктивной реактивной составляющей полной мощности, параллельно цепи питания включается конденсатор. В масштабах предприятия для компенсации реактивной мощности применяются батареи конденсаторов и других компенсирующих устройств.
- Коррекция нелинейности потребления тока в течение периода колебаний питающего напряжения. Если нагрузка потребляет ток непропорционально приложенному напряжению, для повышения коэффициента мощности требуется схема пассивного (PPFC) или активного корректора коэффициента мощности (APFC). Простейшим пассивным корректором коэффициента мощности является дроссель с большой индуктивностью, включённый последовательно с питаемой нагрузкой. Дроссель выполняет сглаживание импульсного потребления нагрузки и выделение низшей, то есть основной, гармоники потребления тока, что и требуется (правда, это достигается в ущерб форме напряжения, поступающего на вход устройства). Активная коррекция коэффициента мощности ценой некоторого усложнения схемы устройства способна обеспечивать наилучшее качество коррекции, приближая коэффициент мощности к 1.
Навигация¶
-
2020/08/04 12:53 Obsidian обновил страницу Напорные пожарные рукава. 2020/04/17 12:44 Obsidian обновил страницу АИГС ГраФиС. 2020/01/19 16:59 Obsidian обновил страницу Коэффициент сжимаемости воздуха. 2019/08/17 15:24 Obsidian обновил страницу Ствол А. 2019/08/17 15:24 Obsidian обновил страницу Ствол Б. 2019/07/18 10:44 Aleksey обновил страницу Линейная скорость распространения горения. 2019/04/10 14:10 Obsidian обновил страницу Сибирская Пожарно-спасательная академия (Сибирская Пожарно-спасательная академия). 2019/01/23 15:56 Obsidian обновил страницу Онлайн калькулятор ГДЗС. 2019/01/23 09:32 Obsidian обновил страницу АИГС ГраФиС. 2018/12/04 11:01 Obsidian обновил страницу Приборы подачи огнетушащих веществ. 2018/11/11 16:12 Obsidian обновил страницу Путь пройденный огнем. 2018/11/11 16:08 Obsidian обновил страницу Онлайн калькулятор ГДЗС. 2018/11/04 20:15 Obsidian обновил страницу Онлайн калькулятор ГДЗС. 2018/09/03 11:21 Obsidian обновил страницу Насосно-рукавные системы. 2018/08/27 09:34 Obsidian обновил страницу Тушение пожаров в зданиях с навесными вентилируемыми фасадами. 2018/07/31 16:54 Obsidian обновил страницу Расчеты параметров работы в СИЗОД. 2018/07/31 15:00 Obsidian обновил страницу Расчеты параметров работы в СИЗОД. 2018/07/24 09:26 Obsidian обновил страницу Расчеты параметров работы в СИЗОД. 2018/07/17 14:46 Obsidian обновил страницу Расчеты параметров работы в СИЗОД. 2018/06/19 20:56 Tor обновил страницу Совмещенный график тушения пожара изменения площади пожара, требуемого и фактического расхода огнетушащих веществ во времени. - Случайная страница
- Новая страница
- Все страницы
- Категории
- Файлы
-
- АА-12,0-60 (63501)
- АА-13/60 (6560)
- АА 8,5-70(43118) — Пожавто
- АБР-5(4308)
- АМО-Ф-15
- АЦ 1,6-40(33081)ПМ-623
- АЦ 2,5-40(433440)
- АЦ 3,0-40(433362)ПМ-574
- АЦ 5,0-40(5557)
- АЦ-1,0-40/4(C41R13)27845F–«Тайга»
- АЦ 2,3-4(33086)
- АЦ-3,0-40(43502)НЕФАЗ
- АЦ-5,0-50/7 (AD190T33) модель 003Б-ЧС
- АЦ-8-40(53215)
- АЦ-2,0-40(4308)004-МС
- АЦ-2,2-40(33081)
- АЦ-2,5-40(433362)ПМ-540
- АЦ 2,5-40(433442)ПМ-548В
- АЦ-3,0-40(4326)ПМ-536
- АЦ-3,2-40/4 CAFS(43253)007-МС
- АЦ-4,0-40(433112)ПМ-599
- Водяные пожарные стволы
- Глубина тушения
- Дехтерев Владимир Владимирович
- Звено ГДЗС
- Испытание противопожарного водопровода на водоотдачу
- ИТС-50-8
- ИТС-70-15
- Заровный Владимир
- 23.02.1991 Пожар в гостинице «Ленинград»
- КУРС-8
- Лестница штурмовая
- Ликвидация горения
- Новости
- Новости-2016
- Нормативы по ГДЗС
- НЦПН-70/100М
- Определение предельного расстояния подачи ОТВ
- Определение расхода воды из пожарных стволов
- ОРТ-50
- Площадь тушения
- Пожарные автомобили порошкового тушения
- Приборы подачи огнетушащих веществ
- Расчет требуемого количества автоцистерн для организации подвоза воды к месту пожара
- РС-50
- РС-70
- РСК-50
- РСКЗ-70
- РСКУ-50А
- РСКУ-50А-АП «ПРОРЫВ»
- РСП-50
- РСП-70
- Рукав А
- Рукав Б
- Статистика пожаров РФ 2013
- Ствол А
- Ствол Б
- Степень тяжести выполняемых в СИЗОД работ
- Условный проход пожарных стволов
- Фактический расход огнетушащих веществ
- ШТОРМ РСП-50А-16н
- ШТОРМ РСП-50А-20
- ШТОРМ РСП-50А-6н
- ШТОРМ РСП-50А-8
- ШТОРМ РСП-50АД-20
- ШТОРМ-РСП-50В
- ШТОРМ РСП-50В-12
- ШТОРМ РСП-50В-12н
- ШТОРМ РСП-50В-2,5
- ШТОРМ РСП-50В-8
- ШТОРМ РСП-50В-8н
- ШТОРМ РСП-80А-16н
- ШТОРМ РСП-80А-20
- ШТОРМ РСП-80В-16
Страницы на которых имеются ссылки на данную статью
-
- Вода — огнетушащее вещество
- АИГС ГраФиС
- ИТС-50-8
- ИТС-70-15
- Классификация пожарной техники
- КУРС-8
- Огнетушащие вещества
- ОРТ-50
- Пена
- Пожарные автомобили
- Пожарные рукава
- Приборы подачи огнетушащих веществ
- РС-50
- РС-70
- РСК-50
- РСКЗ-70
- РСКУ-50А
- РСКУ-50А-АП «ПРОРЫВ»
- РСП-50
- РСП-70
- Рукавные линии
- Стволы воздушно-пенные
- Условный проход пожарных стволов
- ШТОРМ РСП-50А-16н
- ШТОРМ РСП-50А-20
- ШТОРМ РСП-50А-6н
- ШТОРМ РСП-50А-8
- ШТОРМ РСП-50АД-20
- ШТОРМ РСП-50В-12
- ШТОРМ РСП-50В-12н
- ШТОРМ РСП-50В-2,5
- ШТОРМ РСП-50В-8
- ШТОРМ РСП-50В-8н
- ШТОРМ РСП-80А-16н
- ШТОРМ РСП-80А-20
- ШТОРМ РСП-80В-16
Страницы на которые ссылается данная статья
Поиск по сайту
Фазовая цепь RC
Схема слева показывает одну сеть резистор-конденсатор, выходное напряжение которой «опережает» входное напряжение на угол менее 90 o . Идеальная однополюсная RC-цепь будет производить фазовый сдвиг точно на 90 o , а поскольку для колебаний требуется 180 o фазового сдвига, в конструкции RC-генератора необходимо использовать как минимум два однополюсных.
Однако в действительности трудно получить ровно 90 o фазового сдвига, поэтому используется больше стадий. Величина фактического фазового сдвига в цепи зависит от значений резистора и конденсатора, а выбранная частота колебаний с фазовым углом ( Φ ) задается как:
Где: X C — емкостное сопротивление конденсатора, R — сопротивление резистора, а ƒ — частота.
В нашем простом примере выше значения R и C были выбраны таким образом, чтобы на требуемой частоте выходное напряжение опережало входное напряжение под углом около 60 o . Затем фазовый угол между каждым последующим участком RC увеличивается еще на 60 o,, давая разность фаз между входом и выходом 180 o (3 x 60 o ), как показано на следующей векторной диаграмме.
Векторная диаграмма
Затем, соединяя вместе три такие RC-сети последовательно, мы можем произвести полный фазовый сдвиг в цепи 180 o на выбранной частоте, и это образует основы «генератора фазового сдвига», иначе называемого RC-генератором .
Мы знаем, что в схеме усилителя, использующей биполярный транзистор или операционный усилитель, он будет производить сдвиг фазы на 180 o между своим входом и выходом. Если трехступенчатая RC-сеть с фазовым сдвигом подключена между этим входом и выходом усилителя, общий фазовый сдвиг, необходимый для регенеративной обратной связи, составит 3 x 60 o + 180 o = 360 o, как показано ниже.
Три каскада RC каскадно соединены, чтобы получить необходимый наклон для стабильной частоты колебаний. Сдвиг фазы контура обратной связи составляет -180 o, когда фазовый сдвиг каждой ступени составляет -60 o . Это происходит, когда ω = 2πƒ = 1.732 / RC ( tan 60 o = 1.732 ). Затем для достижения требуемого фазового сдвига в цепи генератора RC необходимо использовать несколько RC-фазосдвигающих сетей, таких как схема ниже.
Порядок выполнение работы
1. Определить период прямоугольных импульсов генератора.
С выхода генератора 3Гподать сигнал на вход “Y” осциллографа (рис.18).
При минимальной синхронизации получить на экране 1-2 периода в режиме непрерывной развертки
Определить период сигнала T
, длительность импульса tu
, скважность Q
=
T
t
u
,
используя калибровку развертки осциллографа. Результат записать в таблицу 1
Т а б л и ц а 1
|
tu |
|||
Повторить определение параметров прямоугольного импульса для трех значений tu
.
Результаты занести в таблицу 1.
2. Изучение процесса заряда катушки индуктивности через сопротивление.
Собрать электрическую схему (рис.19) с катушкой индуктивности L
.
Сопротивление цепи R
подобрать так, чтобы на экране осциллографа наблюдалась картина изменения напряжения UL
.
Изменяя сопротивление R
(установить R
1
,
R
2
,
R
3
), зарисовать полученные осциллограммы. Сравнить величины t
z
(рассчитанные по формуле 17
) и экспериментальные данные и записать в таблицу 2.
Таблица 2
|
t |
t |
||
|
R |
|||
|
R |
|||
|
R |
3. Изучение процесса заряда конденсатора через сопротивление.
Собрать электрическую цепь по схеме рис. 20 с конденсатором C
= 6800 пФ.
Сопротивление цепи R
подобрать так, чтобы t
с
T
/ 2,
гдеT
—
периодсигнала.
t
с
=
RC
= (0,1
¸
0,2)
×
T
/ 2
Определить R
по этой формуле. Получить на экране осциллографа в режиме непрерывной развертки картину изменения напряжения при заряде конденсатора. Зарисовать картину в тетради.
Оценить по рисунку t
с
цепи, используя выражения
U
с
(t
с
)
0,63
U
(заряд)
U
с
(t
с
)
0,37
U
(разряд)
Результаты занестив таблицу 3.
Таблица 3
|
t |
t |
||
Аналогичные расчеты провести с конденсаторами С2
и С3.
Сравнить полученные картины. Изменяя R
(в сторону увеличения) зарисовать полученные осциллограммы, отмечая t
с
.
4. Изучение работы интегрирующей цепи.
Интегрирующая цепь удовлетворительна, если постоянная t
с
=
RC
приблизительно равна или больше периода сигналаT
,
т. е. t
с
=
RC
=
T
.
Собрать схему по рис. 20 с элементами C
= 0,01 мкФ,
R
подобрать, исходя из соотношения R
=
T
C
.
Зарисовать полученную на экране осциллографа картину. Зарисовать зависимостьU
вх
(t
)
; ò
U
вх
(t
)
dt
.
5. Изучение работы дифференцирующей цепи.
Собрать электрическую цепь по схеме (рис.21) с конденсатором С1 = 0,1 мкФ.
Сопротивление R
определяем из условия t
с
=
RC
= (0,1
¸
0,2)
T
/2.
Зарисовать кривую тока заряда конденсатора и оценитьt
с
.
Занести результаты в таблицу 4.
Таблица 4
|
t |
||
|
С1 = 0,1 мкФ |
||
|
С2 = 6800 пФ |
Для дифференцирования сигнала в виде прямоугольного импульса необходимо выполнение условия t
ф
>>
RC
=
t
с
,
гдеt
ф
—
фрект импульса.
Обычно ограничиваются условием t
с
=
RC
= (0,01
¸
0,02)
T
.
Собрать схему по рис. 21 с конденсатором С = 0,01 мкФ,
подобрать сопротивление R
, получить на экране осциллографа картину и зарисовать ее.
Внести сопротивление R
1
(увеличивая его) и зарисовать графики U
вх
(t
)
и dU
вх
(t
) /
dt
.
Навигация¶
-
2020/08/04 12:53 Obsidian обновил страницу Напорные пожарные рукава. 2020/04/17 12:44 Obsidian обновил страницу АИГС ГраФиС. 2020/01/19 16:59 Obsidian обновил страницу Коэффициент сжимаемости воздуха. 2019/08/17 15:24 Obsidian обновил страницу Ствол А. 2019/08/17 15:24 Obsidian обновил страницу Ствол Б. 2019/07/18 10:44 Aleksey обновил страницу Линейная скорость распространения горения. 2019/04/10 14:10 Obsidian обновил страницу Сибирская Пожарно-спасательная академия (Сибирская Пожарно-спасательная академия). 2019/01/23 15:56 Obsidian обновил страницу Онлайн калькулятор ГДЗС. 2019/01/23 09:32 Obsidian обновил страницу АИГС ГраФиС. 2018/12/04 11:01 Obsidian обновил страницу Приборы подачи огнетушащих веществ. 2018/11/11 16:12 Obsidian обновил страницу Путь пройденный огнем. 2018/11/11 16:08 Obsidian обновил страницу Онлайн калькулятор ГДЗС. 2018/11/04 20:15 Obsidian обновил страницу Онлайн калькулятор ГДЗС. 2018/09/03 11:21 Obsidian обновил страницу Насосно-рукавные системы. 2018/08/27 09:34 Obsidian обновил страницу Тушение пожаров в зданиях с навесными вентилируемыми фасадами. 2018/07/31 16:54 Obsidian обновил страницу Расчеты параметров работы в СИЗОД. 2018/07/31 15:00 Obsidian обновил страницу Расчеты параметров работы в СИЗОД. 2018/07/24 09:26 Obsidian обновил страницу Расчеты параметров работы в СИЗОД. 2018/07/17 14:46 Obsidian обновил страницу Расчеты параметров работы в СИЗОД. 2018/06/19 20:56 Tor обновил страницу Совмещенный график тушения пожара изменения площади пожара, требуемого и фактического расхода огнетушащих веществ во времени. - Случайная страница
- Новая страница
- Все страницы
- Категории
- Файлы
-
- Глубина тушения
- Ликвидация горения
- Огнетушители
- Определение предельного расстояния подачи ОТВ
- Определение расхода воды из пожарных стволов
- Площадь пожара
- Пожар
- Путь пройденный огнем
- Расчет фактической скорости распространения горения
- Расчет формы пожара
- Совмещенный график тушения пожара изменения площади пожара, требуемого и фактического расхода огнетушащих веществ во времени
- Требуемый расход огнетушащих веществ
Страницы на которых имеются ссылки на данную статью
-
- Глубина тушения
- Интенсивность подачи огнетушащих веществ
- Линейная скорость распространения горения
- Локализация пожара (действия)
- Огнетушащие вещества
- Площадь пожара
- Приборы подачи огнетушащих веществ
- Путь пройденный огнем
- Решающее направление
- Ручные пожарные стволы
- Тушение пожара
Страницы на которые ссылается данная статья
Поиск по сайту
Особые режимы работы цепи
Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:
Примечания
- Нулевая частота в объяснениях поведения этой цепи означает постоянный ток. Если f = 0, предполагается, что цепь подключена к идеальному источнику напряжения.
- При нулевой частоте реактивное сопротивление идеальной катушки индуктивности считается бесконечно большим, если ее индуктивность бесконечно большая. Если же индуктивность катушки конечная или нулевая, ее реактивное сопротивление при нулевой частоте равно нулю и для источника постоянного напряжения она представляет собой короткое замыкание.
Теоретическое обоснование¶
QКачалов А.А. и др. Противопожарное водоснабжение: Учеб. Для пожарно-техн. Училищ / А.А. Качалов, Ю.В. Воротынцев, А.В. Власов. – М.: Стройиздат, 1985-286 с., ил.Тарасов-Агалаков Н.А., Практическая гидравлика в пожарном деле. / Н.А. Тарасов-Агалаков – М.:Издательство Министерства коммунального хозяйства РСФСР, 1959.-263с.Ходаков В.Ф. Гидравлика в пожарном деле. / В.Ф. Ходаков – М.:Высшая школа МООП РСФСР, 1965.-204с.
| (1) |
ω – площадь живого сечения насадка, м2;
g – ускорение свободного падения м/с2;
H – давление перед насадком, МПа.
| (2) |
Горбань Ю.И. Пожарные роботы и ствольная техника в пожарной автоматике и пожарной охране. – М.: Пожнаука, 2013. – 352с.
| (3) |
формуле 3
| (4) |
Q23
| (5) |
r – радиус сердечника, м;
k – конструктивный коэффициент насадка.
5Rrk
| (6) |
формула 3
Экспериментальное измерение импеданса
Прямое измерение импеданса требует измерения амплитуд синусоидальных напряжения и тока изучаемого двухполюсника, и одновременного измерения сдвига фазы между ними.
Импеданс также часто измеряют компенсационными методами с помощью мостов переменного тока, подобными мосту Уитстона для постоянного тока, при таких измерениях мост балансируют изменением эталонных реактивного и активного элементов, по величине реактивного и активного сопротивления эталонных элементов, требуемого для балансировки моста, определяется измеряемый импеданс.
В силовых устройствах измерение импеданса может потребовать одновременного измерения и подачи питания на работающее устройство.
Измерение импеданса устройств и линий передач является практической задачей в радиотехнике и других областях.
Измерения импеданса обычно проводятся на одной частоте, но если требуется определить зависимость импеданса от частоты, то измерения проводят на нескольких частотах в нужном диапазоне частот.
Активная и реактивная составляющие импеданса обычно выражают в омах, но могут использоваться связанные с импедансом величины, например, в радиотехнике, линиях передачи, коэффициент стоячей волны или коэффициент отражения имеют бо́льшее удобство.
Сопротивление устройства можно рассчитать путем деления комплексных напряжения и тока. Полное сопротивление устройства рассчитывается путем подачи синусоидального напряжения на устройство последовательно с эталонным резистором и измерения напряжений на резисторе и на самом устройстве. Выполнение этого измерения на нескольких частотах тестирующего сигнала обеспечивает определение фазового сдвига и величины импеданса.
Измерение отклика исследуемой цепи на импульсный тестирующий сигнал можно использовать в сочетании с быстрым преобразованием Фурье для измерения импеданса различных электрических устройств.
LCR-измеритель (индуктивность L, емкость C и сопротивление R) или измеритель иммитанса — это устройство, обычно используемое для измерения индуктивности, сопротивления и ёмкости компонента. Из этих значений можно рассчитать полное сопротивление на любой частоте.
Дифференцирующая RC-цепь.
Из названия цепи, в принципе, уже понятно, что за элементы входят в ее состав – это конденсатор и резистор И выглядит она следующим образом:
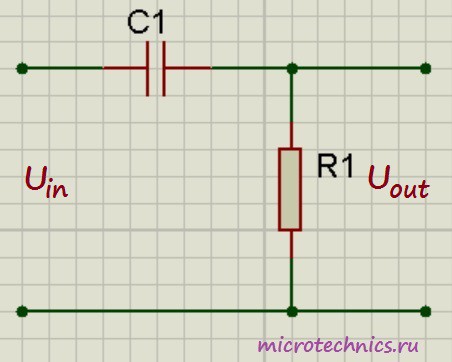
Работа данной схемы основана на том, что ток, протекающий через конденсатор, прямо пропорционален скорости изменения напряжения, приложенного к нему:
i = C\medspace\frac{dU_c}{dt}
Напряжения в цепи связаны следующим образом (по закону Кирхгофа):
u_{out} = u_{in}\medspace-\medspace u_c
В то же время, по закону Ома мы можем записать:
u_{out} = i R = C R\medspace\frac{dU_c}{dt}
Выразим u_c из первого выражения и подставим во второе:
u_{out} = C R\medspace\frac{dU_c}{dt} = C R\medspace(\frac{dU_{in}}{dt}\medspace-\medspace \frac{dU_{out}}{dt}\medspace)
u_{out} = C R\medspace\frac{dU_{in}}{dt}\medspace-\medspace C R\medspace\frac{dU_{out}}{dt}
При условии, что C R\medspace\frac{dU_{out}}{dt} << u_{out} (то есть скорость изменения напряжения низкая) мы получаем приближенную зависимость для напряжения на выходе:
u_{out} \approx C R\medspace\frac{dU_{in}}{dt}
Таким образом, цепь полностью оправдывает свое название, ведь напряжение на выходе представляет из себя дифференциал входного сигнала. Но возможен еще и другой случай, когда C R\medspace\frac{dU_{out}}{dt} >> u_{out} (быстрое изменение напряжения). При выполнении этого равенства мы получаем такую ситуацию:
C R\medspace\frac{dU_{in}}{dt} = C R\medspace\frac{dU_{out}}{dt}
То есть: U_{out} \approx U_{in}.
Можно заметить, что условие C R\medspace\frac{dU_{out}}{dt} << u_{out} будет лучше выполняться при небольших значениях произведения C R, которое называют постоянной времени цепи:
\tau = R C
Давайте разберемся, какой смысл несет в себе эта характеристика цепи Заряд и разряд конденсатора происходит по экспоненциальному закону:
u = U_0\medspace e^{-t/\tau}
Здесь U_0 – напряжение на заряженном конденсаторе в начальный момент времени. Теперь посмотрим, каким будет значение напряжения по истечении времени \tau:
U_{\tau} = U_0\medspace e^{-\tau/\tau} = U_0\medspace e^{-1} \approx 0.37\medspace U_0
Напряжение на конденсаторе уменьшится до 37% от первоначального. Таким образом, \tau – это время, за которое конденсатор:
- при заряде – зарядится до 63%
- при разряде – разрядится на 63% (разрядится до 37%)
С постоянной времени цепи мы разобрались, давайте вернемся к дифференцирующей RC-цепи. Теоретические аспекты функционирования мы разобрали, так что давайте посмотрим, как она работает на практике. А для этого попробуем подавать на вход какой-нибудь сигнал и посмотрим, что получится на выходе. В качестве примера, подадим на вход последовательность прямоугольных импульсов:
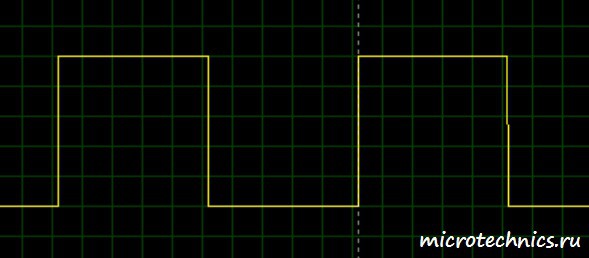
А вот как выглядит осциллограмма выходного сигнала (второй канал – синий цвет):
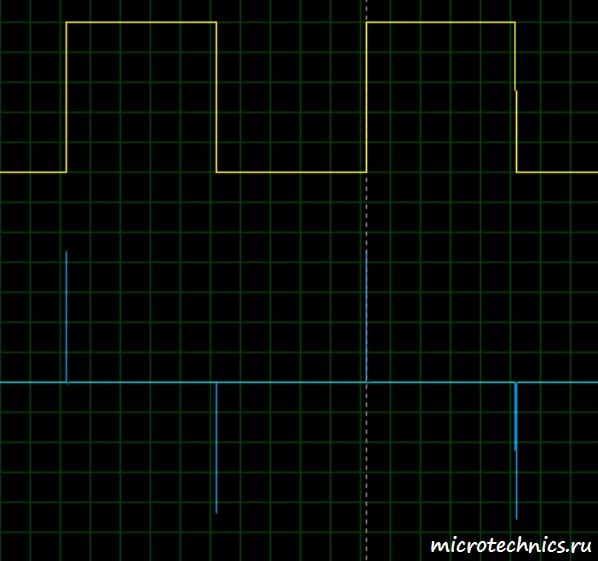
Что же мы тут видим?
Большую часть времени напряжение на входе неизменно, а значит его дифференциал равен 0 (производная константы = 0). Именно это мы и видим на графике, значит RC-цепь выполняет свою дифференцирующую функцию. А с чем же связаны всплески на выходной осциллограмме? Все просто – при “включении” входного сигнала происходит процесс зарядки конденсатора, то есть по цепи проходит ток зарядки и напряжение на выходе максимально. А затем по мере протекания процесса зарядки ток уменьшается по экспоненциальному закону до нулевого значения, а вместе с ним уменьшается напряжение на выходе, ведь оно равно U_{out} = i R. Давайте увеличим масштаб осциллограммы и тогда мы получим наглядную иллюстрацию процесса зарядки:
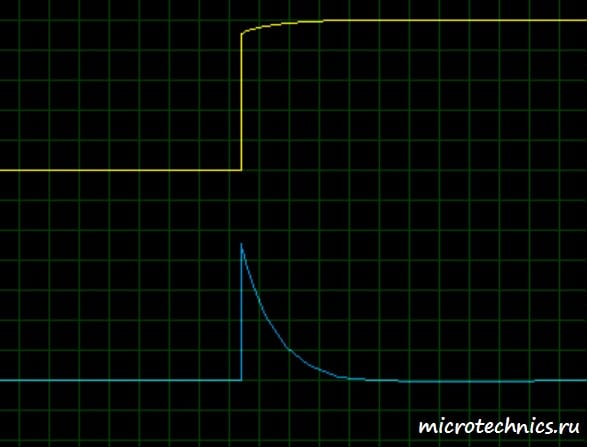
При “отключении” сигнала на входе дифференцирующей цепи происходит аналогичный переходный процесс, но только вызван он не зарядкой, а разрядкой конденсатора.
В данном случае постоянная времени цепи у нас имеет небольшую величину, поэтому цепь хорошо дифференцирует входной сигнал. По нашим теоретическим расчетам, чем больше мы будем увеличивать постоянную времени, тем больше выходной сигнал будет похож на входной. Давай проверим это на практике! Будем увеличивать сопротивление резистора, что и приведет к росту \tau:

Тут даже не надо ничего комментировать – результат налицо Мы подтвердили теоретические выкладки, проведя практические эксперименты, так что давайте переходить к следующему вопросу – к интергрирующим RC-цепям.
Дифференцирующая RC-цепь
Дифференцирующая RC-цепь получается, если поменять местами резистор R и конденсатор С в интегрирующей цепи. При этом входной сигнал идёт на конденсатор, а выходной снимается с резистора. Для постоянного напряжения конденсатор представляет собой разрыв цепи, то есть постоянная составляющая сигнала в цепи дифференцирующего типа будет отсечена. Такие цепи являются фильтрами верхних частот. И частота среза в них определяется всё той же постоянной времени τ{\displaystyle \tau }. Чем больше τ{\displaystyle \tau }, тем ниже частота, которая может быть без изменений пропущена через цепь.
Дифференцирующие цепи имеют ещё одну особенность. На выходе такой цепи один сигнал преобразуется в два последовательных скачка напряжения вверх и вниз относительно базы с амплитудой, равной входному напряжению. Базой является либо положительный вывод источника, либо «земля», в зависимости от того, куда подключён резистор. Когда резистор подключён к источнику, амплитуда положительного выходного импульса будет в два раза выше напряжения питания. Этим пользуются для умножения напряжения, а также, в случае подключения резистора к «земле», для формирования двуполярного напряжения из имеющегося однополярного.