Магнитная цепь

Напряжение — магнитное поле

Напряжение магнитного поля, или магнитное напряжение, в поле между двумя точками определяется работой сил магнитного поля при перемещении единичного ( пробного) магнитного потока между этими точками.
 

Изменяя напряжение магнитного поля, заставляют разделенный поток ионов проходить мимо щели, через которую ионы попадают в камеру, соединенную с регистрирующим устройством.
 

Рассмотрим теперь напряжение магнитного поля в этом случае.
 

Так как напряжение магнитного поля Н перпендикулярно к п и к D, то каждая из осей полученного в сечении эллипса дает также направление магнитного напряжения, соответствующее электрической индукции, направление которой совпадает с другой осью. В то же время направление напряжения электрического поля Е согласно ( 260) задается нормалью к эллипсоиду в конце той оси, которая определяет электрическую индукцию.
 

Таким образом, напряжение магнитного поля ( и индукция) также перпендикулярно к направлению перемещения и находится в плоскости фронта волны.
 

Я, v напряжения магнитного поля представляют собой косинусы трех взаимно перпендикулярных направлений.
 

Так как вектор напряжения магнитного поля перпендикулярен как к лучу, так и к нормали к волне, и этот вектор определяет направление поляризации, то следовательно направления поляризации являются линиями, перпендикулярными к плоскостям, заключающим нормаль к волне и лучи.
 

Так как вектор напряжения магнитного поля здесь перпендикулярен к лучу, он имеет две составляющие: одну перпендикулярную к плоскости падения и одну в плоскости падения. Мы можем рассмотреть отдельно волны, соответствующие этим двум составляющим.
 

Коллектор ионов.

В нервом случае постепенно изменяют напряжение магнитного поля, вследствие чего на коллектор последовательно попадают пучки ионов изучаемых участков спектра. Кривая величины тока, идущего из коллектора, записывается электронным потенциометром.
 

Динамические петли гистерезиса пластин молибденового пермаллоя толщиной 50 мкм при частотах 5 ( 1, 25 ( 2 и 100 ( 3 кГц.

Синхронность в изменении намагниченности и напряжения магнитного поля может иметь место только при очень медленном ( квазистатическом) изменении магнитного поля. В случае переменных магнитных полей указанная синхронность отсутствует и форма динамической петли гистерезиса зависит от формы образца и от частоты переменного поля. Опыт показывает, что магнитная проницаемость существенно зависит от частоты переменного поля даже в том случае, когда исключено влияние токов Фуко.
 

Мы видим, что направление напряжения магнитного поля играет особую роль. Это объясняется тем, что направление его совпадает с направлением магнитной индукции, в то время как направление напряжения электрического поля, вообще говоря, не совпадает с направлением электрической индукции.
 

Итак, напряжение электрического поля и напряжение магнитного поля являются взаимно перпендикулярными. Любое из них может быть принято за световой вектор.
 

Например, течение реакций зависит также от напряжения окружающего магнитного поля, меняющегося в зависимости от времени в соответствии с характером движения Земли в космическом пространстве.
 

Процесс сборки

Сборка предполагает использование макетной платы размером не менее 15 x 24 отверстия, и особое внимание обращается на расположение элементов на ней. На фотографиях показано рекомендуемое расположение каждого из радиоэлементов и какие связи между ними выполнить

Перемычки на печатной плате можно выполнить из фрагментов кабеля или отрезанных ножек от других элементов (резисторы, конденсаторы), которые остались после их монтажа.

Сначала надо впаять катушки L1 и L2. Хорошо отодвинуть их друг от друга, что даст нам пространство и увеличит эффект стерео. Эти катушки являются ключевым элементом схемы — они ведут себя как антенны, которые собирают электромагнитное излучение из окружающей среды.

После впайки катушек можно установить конденсаторы C1 и C2. Их емкость составляет 2,2 мкФ и определяет нижнюю частоту среза звуков, которые будут услышаны в наушниках. Чем выше значение ёмкости, тем ниже звуки воспроизводящиеся в системе. Большая часть мощного электромагнитного шума лежит на частоте 50 Гц, так что есть смысл его отфильтровать.

Далее припаиваем резисторы по 1 кОм — R1 и R2. Резисторы эти, вместе с R3 и R4 (390 кОм) определяют усиление операционного усилителя в схеме. Инвертирование напряжения не имеет в нашей системе особого значения.

Виртуальная масса — резисторы R5 и R5 с сопротивлением 100 кОм. Они являются простым делителем напряжения, который в данном случае будет делить напряжение 9 V на половину, так что с точки зрения схемы питается м/с напряжением -4,5 V и +4,5 V по отношению к виртуальной массе.

Можно поставить в панельку операционный усилитель любой со стандартными выводами, например OPA2134, NE5532, TL072 и другие.

Подключаем аккумулятор и наушники — теперь мы можем использовать этот акустический монитор для прослушки электромагнитных полей. Батарею можно приклеить к плате скотчем.

Соленоид

Соленоид отличается от обычной катушки по двум признакам:

• Длина обмотки превышает диаметр в несколько раз;
• Толщина обмотки меньше диаметра катушки также в несколько раз.

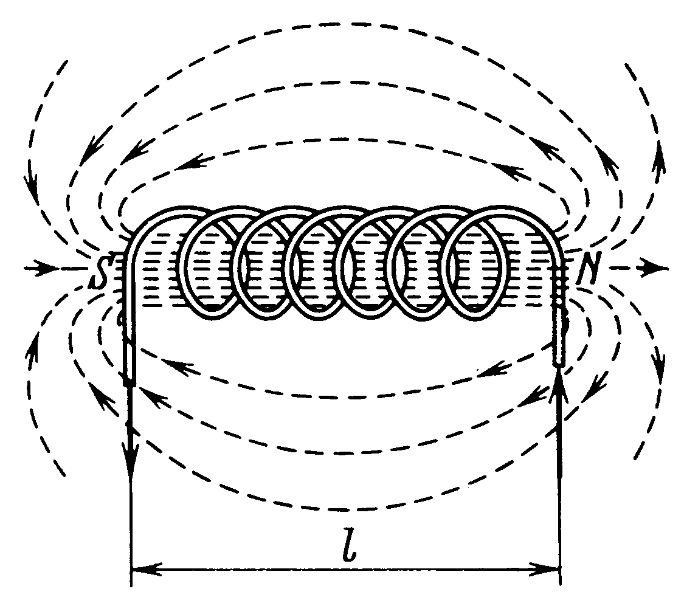
Соленоидальный тип катушки

Параметры соленоида можно узнать из такого выражения:

L=µ0N2S/l,

где:

• µ0 – магнитная постоянная;
• N – количество витков;
• S – площадь поперечного сечения обмотки;
• l – длина обмотки.

Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника

Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.

Колебательный контур

Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.

Последовательный и параллельный колебательные контуры

Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.

Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.

Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.

Q-метр для измерения добротности

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

L=Ф/I.

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

L=L1∙N2.

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

Сила Лоренца

Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.

Формула для нахождения силы Лоренца:

где ​\( q \)​ – заряд частицы, ​\( v \)​ – скорость частицы, ​\( B \)​ – модуль вектора магнитной индукции, ​\( \alpha \)​ – угол между вектором скорости частицы и вектором магнитной индукции.

Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ​\( B_\perp \)​ входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.

Если заряд частицы отрицательный, то направление силы изменяется на противоположное.

Важно! Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно. В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы

В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы.

Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен:

где ​\( m \)​ – масса частицы, ​\( v \)​ – скорость частицы, ​\( B \)​ – модуль вектора магнитной индукции, ​\( q \)​ – заряд частицы.

В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы:

Угловая скорость движения заряженной частицы:

Важно! Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы

Если вектор скорости направлен под углом ​\( \alpha \)​ (0° < \( \alpha \) < 90°) к вектору магнитной индукции, то частица движется по винтовой линии.

В этом случае вектор скорости частицы можно представить как сумму двух векторов скорости, один из которых, ​\( \vec{v}_2 \)​, параллелен вектору \( \vec{B} \), а другой, \( \vec{v}_1 \), – перпендикулярен ему. Вектор \( \vec{v}_1 \) не меняется ни по модулю, ни по направлению. Вектор \( \vec{v}_2 \) меняется по направлению. Сила Лоренца будет сообщать движущейся частице ускорение, перпендикулярное вектору скорости \( \vec{v}_1 \). Частица будет двигаться по окружности. Период обращения частицы по окружности – ​\( T \)​.

Таким образом, на равномерное движение вдоль линии индукции будет накладываться движение по окружности в плоскости, перпендикулярной вектору \( \vec{B} \). Частица движется по винтовой линии с шагом ​\( h=v_2T \)​.

Важно! Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна:

Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак».

Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы:

• сделать чертеж, указать на нем силовые линии магнитного (и электрического) поля, нарисовать вектор начальной скорости частицы и отметить знак ее заряда;
• изобразить силы, действующие на заряженную частицу;
• определить вид траектории частицы;
• разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному;
• составить основное уравнение динамики материальной точки по каждому из направлений разложения сил;
• выразить силы через величины, от которых они зависят;
• решить полученную систему уравнений относительно неизвестной величины;
• решение проверить.

«Действие магнитного поля на проводник с током»

Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.

Сила Ампера зависит от длины проводника с током, силы тока в проводнике, модуля магнитной индукции и расположения проводника относительно линий магнитной индукции: F_A = BIlsinа.

Для определения направления силы Ампера применяют правило левой руки. Если левую руку расположить в магнитном поле так, чтобы силовые линии входили в ладонь, а четыре пальца были направлены по току, то отогнутый большой палец укажет направление силы, действующей на проводник.

Магнитное взаимодействие можно наблюдать между двумя параллельными токами (опыт Ампера): два параллельных проводника с током отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают.

Экспериментальное исследование показывает, что сила Ампера прямо пропорциональна длине проводника l и силе тока I в проводнике. Коэффициентом пропорциональности в этом равенстве является модуль вектора магнитной индукции В. Соответственно, F = BIl. В таком виде зависимость силы, действующей на проводник с током в магнитном поле, записывается в том случае, если линии магнитной индукции перпендикулярны проводнику с током. Из приведённой формулы понятно, что магнитная индукция является силовой характеристикой магнитного поля.

Единица магнитной индукции =  1Н / 1А • 1м = 1 Тл. За единицу магнитной индукции принимают магнитную индукцию такого поля, в котором на проводник длиной 1 м действует сила 1Н при силе тока в проводнике 1 А.

Магнитное поле действует также на движущиеся заряженные частицы. При этом сила (сила Лоренца) зависит от модуля магнитной индукции, заряда частицы, а также от модуля и направления её скорости.

Электрический двигатель

Движение проводника с током в магнитном поле лежит в основе работы электрического двигателя. Если поместить прямоугольную рамку в магнитное поле и пропустить по ней электрический ток, то рамка повернётся, потому, что на стороны рамки действует сила Ампера. При этом сила, действующая на сторону рамки ab, противоположна силе, действующей на сторону cd.

Для того чтобы рамка не остановилась в тот момент, когда её плоскость перпендикулярна линиям магнитной индукции, и продолжала вращаться, изменяют направление тока в проводнике. Для этого к концам рамки припаяны полукольца, по которым скользят контакты, соединённые с источником тока. При повороте рамки на 180° меняются контактные пластины, которых касаются полукольца и, соответственно, направление тока в рамке.

В электрическом двигателе энергия электрического и магнитного полей превращается в механическую энергию.

Действие магнитного поля на проводник с током

Конспект урока по физике в 8 классе «Действие магнитного поля на проводник с током».

Следующая тема: «Электромагнитная индукция. Опыты Фарадея».

Закон электромагнитной индукции Фарадея

Формула магнитного потока

Отрицательное значение ЭДС – это обозначение противоположного знака по отношению к изменению Ф. Если скажут «запишите формулу закона электромагнитной индукции», следует не забывать о динамической природе рассматриваемого явления. Ниже приведены примеры для вычисления основных электрических параметров:

• ЭДС одиночного контура E1 = – (ΔФ/Δt), где Δt – временной интервал;
• при создании конструкции из N витков EN = – N*(ΔФ/Δt);
• ток в проводнике (замкнутый контур с электрическим сопротивлением R) I = E/R;
• движущийся со скоростью v проводник длиной D создает ЭДС E = В * D * v * sin α.

Устройство электромагнитов

Несмотря на обширное, судя по описанной выше классификации, количество разнообразных вариантов электромагнитов, существуют определенные однотипные узлы, которые встречаются у всех ЭМ.

• Катушка с расположенной на ней намагничивающей обмоткой
• Подвижная часть электромагнита — якорь
• Неподвижная часть — ярмо и сердечник

Между якорем и неподвижными частями существуют воздушные промежутки. Так вот, воздушные промежутки бывают полезными и паразитными. Полезные промежутки располагаются по возможному пути движения якоря. Паразитные промежутки лежат за пределами движения якоря.

Также существует понятие полюса. Полюсами называют поверхности магнитопровода, которые ограничивают полезный воздушный промежуток.

Конструктивные формы электромагнитов переменного тока не имеют множества вариантов, за счет того, что сердечник набирается из листов электротехнической стали. Это необходимо для борьбы с вихревыми токами.

Основные формулы раздела «Электромагнитная индукция»

Для упрощения расчетов ниже приведены алгоритмы тематических вычислений:

• закон магнитной индукции – E = – (ΔФ/Δt);
• магнитный поток – Ф = В * S * cos α;
• закон ЭДС для движущегося проводника – Ev = В * D * v * sin α;
• электродвижущая сила самоиндукции катушки – Ec = -L*(ΔI/Δt);
• магнитный поток (индуктивность) – Ф = L*I (L= Ф/I);
• энергия, которую в соответствии с законом индукции накапливает катушка, – W = (L * I2)/2.

Как использовать приведенные формулы на практике, рассказано выше. В расчетах следует учитывать определенное значение электрических параметров, скорость перемещения и геометрию проводника.

Магнитное поле одиночного витка с током

$inline$B_z(z)$inline$Иллюстрация к закону Био-Савара-Лапласа$inline$O$inline$$inline$C$inline$$inline$a$inline$$inline$I$inline$$inline$\vec{r}$inline$$inline$\vec{r}_0$inline$$inline$\varphi$inline$$inline$\vec{r}$inline$$inline$OX$inline$$inline$\rho$inline$$inline$\mathrm{d}\vec{r}$inline$$inline$\vec{r}$inline$$inline$\mathrm{d}\vec{r}$inline$

$$display$$\mathrm{d}\vec{B}(\vec{r}_0)=\frac{\mu_0 I}{4\pi} \cdot \frac{}{|\vec{r}_0-\vec{r}|^3}$$display$$

$$display$$\vec{r}_0 = (\rho\cos{\varphi}, \rho\sin{\varphi}, z) \overset{\varphi = 0}{\rightarrow} (\rho, 0, z)$$display$$

$$display$$\vec{r} = (a\cos{\varphi}, a\sin{\varphi}, 0)$$display$$

$$display$$\mathrm{d}\vec{r} = (-a\sin{\varphi}, a\cos{\varphi}, 0)\,\mathrm{d}\varphi$$display$$

$$display$$\vec{r}_0-\vec{r} = (\rho -a\cos{\varphi}, -a\sin{\varphi}, z)$$display$$

$$display$$ = \begin{vmatrix} \vec{e}_x& \vec{e}_y& \vec{e}_z\\ -a\sin{\varphi}\,\mathrm{d}\varphi& a\cos{\varphi}\,\mathrm{d}\varphi& 0\\ \rho -a\cos{\varphi}& -a\sin{\varphi}& z \end{vmatrix} = (az\cos{\varphi}, az\sin{\varphi}, a^2 -a\rho\cos{\varphi})\,\mathrm{d}\varphi$$display$$

$$display$$|\vec{r}_0-\vec{r}|^3 = \left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}$$display$$

$$display$$\vec{B}(\vec{r}_0) = \int_C{\,\mathrm{d}\vec{B}(\vec{r}_0)}$$display$$

$$display$$B_z(\rho, z) = \frac{\mu_0 I}{4\pi} \int_0^{2\pi}{\frac{\left( a^2 -\rho a\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}$$display$$

$$display$$B_r(\rho, z) = \frac{\mu_0 I}{4\pi} \int_0^{2\pi}{\frac{a\,z\,\cos{\varphi}\,\mathrm{d}\varphi} {\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}$$display$$

$inline$B = \sqrt{B_r^2 + B_z^2}$inline$$inline$a = 0.1$inline$$inline$I=1$inline$Амплитуда аксиальной компоненты магнитного поляАмплитуда радиальной компоненты магнитного поляАбсолютная амплитуда магнитного поля$inline$z\gg a$inline$
Подсказка…Для подобных вычислений и построения графиков удобно использовать MathCad 15

Самоиндукция. Энергия магнитного поля

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.

Собственный Φ, пронизывающий контур или катушку с током, пропорционален силе тока I

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукциииндуктивностью катушки. Единица индуктивности в СИ называется генри (Гн). Индуктивность контура или катушки равна или 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб

В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой (см. § 1.17)

где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида.

Магнитный поток, пронизывающий все N витков соленоида, равен

Следовательно, индуктивность соленоида равна

где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз (см. § 1.17); поэтому индуктивность катушки с сердечником также увеличивается в μ раз:

ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы (рис. 1.21.1). Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Рисунок 1.21.1. Магнитная энергия катушки. При размыкании ключа K лампа ярко вспыхивает.

Из закона сохранения энергии следует, что вся энергия, запасенная в катушке, выделится в виде джоулева тепла. Если обозначить через R полное сопротивление цепи, то за время Δt выделится количество теплоты ΔQ = I2RΔt.

Ток в цепи равен

Выражение для ΔQ можно записать в виде

В этом выражении ΔI < 0; ток в цепи постепенно убывает от первоначального значения I до нуля. Полное количество теплоты, выделившейся в цепи, можно получить, выполнив операцию интегрирования в пределах от I до 0. Это дает

Эту формулу можно получить графическим методом, изобразив на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, равное первоначальному запасу энергии магнитного поля, определяется площадью изображенного на рис. 1.21.2 треугольника.

Рисунок 1.21.2. Вычисление энергии магнитного поля.

Таким образом, энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна

Применим полученное выражение для энергии катушки к длинному соленоиду с магнитным сердечником. Используя приведенные выше формулы для коэффициента самоиндукции L_μ соленоида и для магнитного поля B, создаваемого током I, можно получить:

где V – объем соленоида. Это выражение показывает, что магнитная энергия локализована не в витках катушки, по которым протекает ток, а рассредоточена по всему объему, в котором создано магнитное поле. Физическая величина

равная энергии магнитного поля в единице объема, называется объемной плотностью магнитной энергии. Дж. Максвелл показал, что выражение для объемной плотности магнитной энергии, выведенное здесь для случая длинного соленоида, справедливо для любых магнитных полей.

Как связана индукция и напряженность магнитного поля?

Магнетиком называется вещество, которое под действием магнитного поля способно намагничиваться (или как говорят физики приобретать магнитный момент). Магнетиками являются практически все вещества. Намагничивание веществ объясняется тем, что в веществах присутствуют свои собственные микроскопические магнитные поля, которые создаются вращением электронов по своим орбитам. Когда внешнее магнитное поле отсутствует, то микроскопические поля расположены произвольным образом, а под воздействием внешнего магнитного поля соответствующим образом ориентируются.

Для характеристики намагничивания различных веществ используют так называемый вектор намагничивания J.

Таким образом, под действием внешнего магнитного поля с магнитной индукцией В, магнетик намагничивается и создает свое магнитное поле с магнитной индукцией В’. В итоге общая индукция В будет состоять из двух слагаемых

Тут возникает проблема вычисления магнитной индукции намагниченного вещества В’, для решения которой необходимо считать электронные микротоки всего вещества, что практически нереально.

Альтернативой данного решения есть ввод вспомогательных параметров, а именно напряженность магнитного поля Н и магнитная восприимчивость χ. Напряженность связывает магнитную индукцию В и намагничивание вещества J следующим выражением

где В – магнитная индукция,

μ – магнитная постоянная, μ = 4π*10-7 Гн/м.

В то же время вектор намагничивания J связан с напряженность магнитного поля В параметром, характеризующим магнитные свойства вещества и называемым магнитной восприимчивостью χ

где J – вектор намагничивания вещества,

μ_r – относительная магнитная проницаемость вещества.

Однако наиболее часто для характеристики магнитных свойств веществ используют относительную магнитную проницаемость μ_r.

Таким образом, связь между напряженностью и магнитной индукцией будет иметь следующий вид

где μ – магнитная постоянная, μ = 4π*10-7 Гн/м,

μ_r – относительная магнитная проницаемость вещества.

Так как намагничивание вакуума равна нулю (J = 0), то напряженность магнитного поля в вакууме будет равна

Отсюда можно вывести выражения напряженности для магнитного поля, создаваемого прямым проводом с током:

где I – ток протекающий по проводнику,

b – расстояние от центра провода до точки, в которой считается напряженность магнитного поля.

Как видно из данного выражения единицей измерения напряженности является ампер на метр (А/м) или эрстед (Э)

Таким образом, магнитная индукция В и напряженность Н являются основными характеристиками магнитного поля, а магнитная проницаемость μ_r – магнитной характеристикой вещества.

Электронное учебное пособие по разделам курса физики Электростатика. Электродинамика. Электромагнетизм. Электромагнитные колебания и волны

47. Магнитное поле электрического тока. Магнитное взаимодействие токов

В древности
магнитами называли куски специальной руды – магнитного железняка, способного
притягивать предметы, изготовленные из железа. В настоящее время используются
магниты различной формы, искусственно изготовленные из различных магнитных
материалов.  Концы магнитов называют полюсами магнита – северный и южный.
Известно, что одноименные полюса магнитов отталкиваются, разноименные – 
притягиваются. Наибольшим магнитом на Земле является сама Земля, тоже имеющая два
полюса. Намагниченный стержень  – стрелка компаса – на Земле располагается так,
что его концы ориентированы к  полюсам Земли.

В 1820 году
датский ученый Эрстед (1777 – 1851) открыл магнитное поле электрического тока.
Это открытие позволило установить связь между электрическими и магнитными
явлениями и построить единую теорию электромагнитного поля.

Электрическое поле
действует как на неподвижные, так и подвижные заряды. В отличие от
электрического поля магнитное поле действует только на движущиеся заряды, т.е.
токи. Действие магнитного поля на проводник с током зависит не только от
величины самого магнитного поля и величины тока, но и от формы проводника и от
расположения его в магнитном поле. Механическое действие, которое магнитное
поле оказывает на разные объекты с током, можно характеризовать вектором силы,
а само магнитное поле – векторной физической величиной, называемой вектором
магнитной индукции. В простейшем случае для изучения
магнитного поля пользуются магнитной стрелкой, северный полюс которой указывает
направление вектора индукции магнитного поля в различных  точках пространства.
Для количественной характеристики магнитного поля пользуются небольшой рамкой с
током, на которую магнитное поле оказывает ориентирующее действие. Вращающий
момент сил, действующих на рамку с током в магнитном поле, пропорционально
вектору индукции магнитного поля. Распределение  вектора магнитной индукции
изучается,  устанавливая рамку в различных точках поля.

На практике
направление вектора индукции магнитного поля, создаваемого проводником с током,
определяется по правилу правого буравчика: если направление поступательного
движения буравчика совпадает с направлением тока в проводнике, то направление
магнитного поля в данной точке совпадает с направлением движения конца рукоятки
буравчика (рис.52).

Рис.52

Единица измерения
индукции магнитного поля в системе «СИ» называется Тесла (Тл).

Вместе с вектором
магнитной индукции магнитное поле характеризуется вектором напряженности
магнитного поля , который связан с вектором магнитной
индукции соотношением

,                                        
(1)

где μ – относительная магнитная
проницаемость среды (величина безразмерная), μ
магнитная постоянная, равная 4π·107 В·с/А·м. Вектор магнитной индукции в
вакууме  связан с вектором магнитной напряженности
соотношением 

.                                              
(2)

.                                          

Из формул (1) и (2) следует, что магнитная
проницаемость среды

                                               
(3)

показывает, во сколько
раз индукция магнитного поля в среде больше,  чем в вакууме. В системе «СИ» за
единицу измерения вектора магнитной напряженности магнитного поля, называемую
«Ампер на метр» (А/м), принимается напряженность такого магнитного поля,
магнитная индукция которого в вакууме равна 4π·10-7 Тл. В системе
СГСМ напряженность магнитного поля измеряется в Эрстедах (Э)

1Э = (103/4π) А/м = 79,6 А/м ≈
80 А/м.

Медицина и вопросы безопасности

Из-за того, что человеческие ткани имеют очень низкий уровень восприимчивости к статическому магнитному полю, не существует научных доказательств его эффективности для использования в лечении любых заболеваний. По той же причине отсутствуют научные свидетельства опасности для здоровья человека, связанной с воздействием этого поля. Однако если ферромагнитное инородное тело находится в человеческих тканях, магнитное поле будет взаимодействовать с ним, что может представлять собой серьёзную опасность.

В частности, если кардиостимулятор был встроен в грудную клетку пациента, следует держать его подальше от магнитных полей. Именно по этой причине больные с установленным кардиостимулятором не могут быть протестированы с использованием МРТ, которое представляет собой магнитное устройство визуализации внутренних органов и тканей.

Дети иногда могут глотать небольшие магниты из игрушек. Это может быть опасно, если ребёнок проглотил два или более магнита, так как магниты могут повредить внутренние ткани; был зафиксирован как минимум один смертельный случай.

Дополнительные возможности

Что можно добавить, чтобы увеличить функциональность? Регулятор громкости — два потенциометра между выходом из схемы и гнездом для наушников. Выключатель питания — сейчас схема включена все время, пока не отсоединится батарейка.

При испытаниях оказалось, что устройство очень чувствительно на источника поля. Вы можете услышать, например, как обновляется экран в мобильном телефоне, или как красиво поет кабель USB во время передачи данных. Приложенный к включенному громкоговорителю работает как обычный и вполне точный микрофон, который собирает эл-магнитное поле катушки работающего динамика.

Хорошо ищет кабеля в стене, на манер трассоискателя. Только надо поднять НЧ, увеличив все 4 ёмкости до 10 мкФ. Недостатком является довольно большой шум и ещё сигнал слишком слабый — нужен какой-то дополнительный усилитель мощности, например на PAM-8403.

Катушка индуктивности. Магнитно-связанные катушки

$inline$n$inline$$inline$OZ$inline$$inline$\delta$inline$$inline$\delta=0,1$inline$Индуктивно связанные катушки$inline$a_1$inline$$inline$n_1$inline$$inline$a_2$inline$$inline$n_2$inline$

$$display$$\Phi = \iint_S{\vec{B}\cdot\vec{\,\mathrm{d}S}} = \int_0^{2\pi}{\int_0^{a-\delta}{B_z(\rho,z)\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi}} = 2\pi\int_0^{a-\delta}{B_z(\rho,z)\rho\,\mathrm{d}\rho}$$display$$

$$display$$\Psi = \frac{1}{2}n^2\mu_0 I \int_0^{a-\delta}{\int_0^{2\pi}{\frac{\left( a^2 — \rho a\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

$inline$L$inline$$inline$\Psi = LI$inline$

$$display$$L_1 = \frac{1}{2}n_1^2\mu_0 \int_0^{a_1-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

$$display$$L_2 = \frac{1}{2}n_2^2\mu_0 \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_2^2 — \rho a_2\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_2^2 -2\rho a_2\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

$inline$d$inline$

$$display$$\Psi_{12} = \frac{1}{2}n_1 n_2\mu_0 I \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 + z^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

$$display$$M_{12} = \frac{1}{2}n_1 n_2\mu_0 \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 + d^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

$inline$\Psi_{12} = \Psi_{21}$inline$$inline$M_{12} = M_{21} = M$inline$

$$display$$k = \frac{M}{\sqrt{L_1L_2}}$$display$$

$inline$a_1 = a_2 = 0.1$inline$$inline$n_1 = n_2 = 100$inline$$inline$L_1 = L_2 = 8.775$inline$Коэффициент связи катушек от расстояния между ними