Круговая поляризация

Содержание:

Особенности диаграммы направленности антенной решётки
Какой тип антенн использовать для квадрокоптера?
Применение антенны поляризации
Поляризация частиц
Практическое значение
История[править]
Плоская спутниковая антенна
Виды поляризации
Параметры Стокса[править]
Практическое значение
Поляризация частиц
Векторы и матрицы Джонса[править | править код]
Линейная поляризация

Особенности диаграммы направленности антенной решётки

ДН$inline$\phi$inline$$inline$w_n=1, n = 1 … N$inline$

$$display$$F(\phi)=|y|^2=\frac{\sin^2(\pi \frac{Nd}{\lambda}\sin\phi)}{\sin^2(\pi \frac{d}{\lambda}\sin\phi)} $$display$$

Периодичность диаграммы направленности

d/λНенормированная диаграмма направленности антенной решётки для N = 5Нормированная диаграмма направленности антенной решётки для N = 5 в полярной системе координатs$inline$e^{i\Psi n}$inline$$inline$\Psi = 2\pi \frac{d}{\lambda}\sin\phi$inline$$inline$\Psi_1 = \Psi_2 + 2\pi m$inline$

Физически: плоские волновые фронты, приходящие с этих направлений, индуцируют на элементах антенной решётки идентичные амплитудно-фазовые распределения электромагнитных колебаний.
Геометрически: для этих двух направлений совпадают.

Связанные подобным образом направления прихода волны являются с точки зрения антенной решётки эквивалентными и не различимы между собой.ДН$inline$-\pi$inline$$inline$\pi$inline$

$$display$$-\pi<2\pi\frac{d}{\lambda}\sin\phi<\pi$$display$$

$$display$$|\sin\phi|<\frac{\lambda}{2d}$$display$$

d/λdλd λОбычно, дифракционные лепестки стремятся подавить с помощью направленных антенных элементов. В этом случае полная диаграмма направленности антенной решётки является произведением ДН одного элемента и решётки изотропных элементов. Параметры ДН одного элемента обычно выбирают исходя из условия на область однозначности антенной решётки.

Ширина главного лепестка

$inline$\Delta \phi ≈ \frac{\lambda}{D}$inline$ДН$inline$F(\phi)$inline$$inline$\sin\phi=m\frac{\lambda}{dN}$inline$Полагая$inline$\frac{\lambda}{dN}<<1$inline$$inline$\Delta \phi = 2\frac{\lambda}{dN}$inline$ДНАР

$$display$$\Delta \phi≈0.88\frac{\lambda}{dN}$$display$$

Равномерное распределение амплитуды (weights 1): $inline$w_n=1$inline$.
Спадающее к краям решётки значения амплитуды (weights 2): $inline$w_n=0.5+0.3\cos(2\pi\frac{n-1}{N}-\pi\frac{N-1}{N})$inline$
Увеличивающиеся к краям решётки значения амплитуды(weights 3): $inline$w_n=0.5-0.3\cos(2\pi\frac{n-1}{N}-\pi\frac{N-1}{N})$inline$

Из рисунка можно проследить следующие тенденции: спадающее к краям решётки распределение амплитуд весовых коэффициентов приводит к уширению главного лепестка ДН, но уменьшению уровня боковых лепестков. Увеличивающиеся к краям антенной решётки значения амплитуд, напротив, приводят к сужению главного лепестка и увеличению уровня боковиков.

Амплитуды весовых коэффициентов всех элементов, кроме крайних, равны нулю. Веса для крайних элементов равны единице. В этом случае решётка становится эквивалентна двухэлементной АР с периодом D = (N-1)d. Не трудно прикинуть по представленной выше формуле ширину главного лепестка. При этом боковики превратятся в дифракционные максимумы и выровнятся по уровню с главным максимумом.
Вес центрального элемента равен единице, а всех остальных – нулю. В этом случае мы получили по сути одну антенну с изотропной диаграммой направленности.

Направление главного максимума

ДН АР$inline$\phi_0$inline$$inline$\textbf{s}(\phi_0)$inline$Nwколлинеарны$inline$\textbf{w}=\beta \textbf{s}(\phi_0)$inline$β
$inline$\textbf{w}=\textbf{s}(10°)$inline$

$$display$$w_n=\exp\{i2\pi\frac{d}{\lambda}(n-1)\sin(10\pi/180)\}$$display$$

ДНОписанную особенность формирования ДН на приём и передачу следует всегда иметь в виду при работе с антенными решётками.

Какой тип антенн использовать для квадрокоптера?

Формулы площади геометрических фигур

Почему не рекомендуется использовать на квадрокоптерах антенны с линейной поляризацией? Все дело в физике. Как уже говорилось выше, линейная поляризация работает в одной плоскости, и чтобы сигнал всегда был сильным, приемник (квадрокоптер) и передатчик (пульт) всегда должны быть параллельны. Но это невозможно из-за специфики полетов дрона. Например, сигнал будет очень плохим, если антенны приемника и передатчика будут под углом 90° друг к другу.

Другое дело с круговой поляризацией, у нее охват гораздо шире, уровень сигнала всегда будет на приемлемом уровне, поэтому все пилоты всегда меняют стандартные антенны на «клевер». На большие дроны-долголеты, которым нужна частота 1.2Ггц, ставят большие клеверы:

Клевер 1.2Ггц

Антенны типа «клевер» бывают с 3 лепестками и 4 лепестками:

Антенна клевер: 3 лепестка и 4 лепестка

Антенна с 4 лепестками обычно используется в качестве принимающей, а 3-лепестковая является универсальной и используется в обоих случаях (прием и отправка).

Общий вид на 3 типа поляризации:

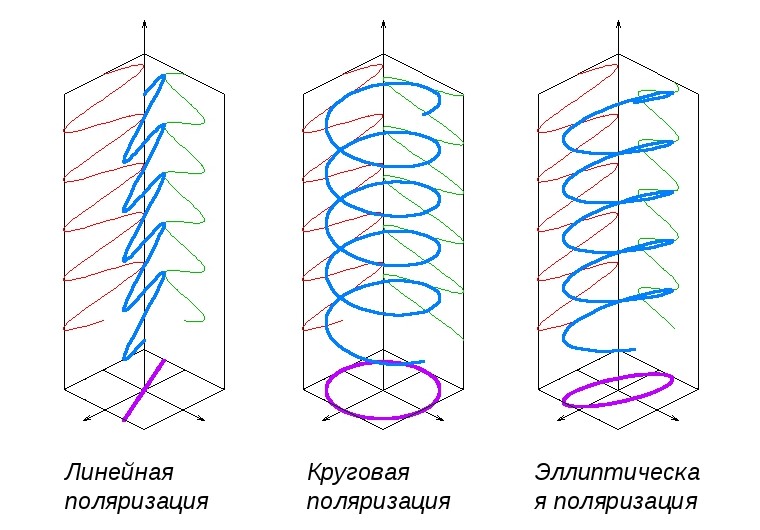
Применение антенны поляризации

Колебательный контур

Различные типы поляризации используются в различных приложениях, с тем чтобы их преимущества, которые будут использоваться. Линейная поляризация на сегодняшний день является наиболее широко используемым для большинства применений радиосвязи. Вертикальная поляризация часто используется для мобильной радиосвязи. Это происходит потому, что многие вертикально поляризованные конструкции антенны имеют всенаправленный диаграмму направленности, и это означает, что антенны не должны быть переориентирован как позиции, как это всегда бывает для мобильной радиосвязи, как передвигается транспортное средство. Для других применений радиосвязи поляризация часто определяется соображениями РЧ антенн. Некоторые большие массивы антенных многоэлементные могут быть установлены в горизонтальной плоскости, более легко, чем в вертикальной плоскости. Это обусловлено тем, что РЧ антенна элементы находятся под прямым углом к вертикальной башне полюса, на котором они установлены, и, следовательно, используя антенну с горизонтальными элементами есть меньше физических и электрических помех между ними. Это определяет стандартную поляризацию во многих случаях.

В некоторых приложениях существует разница в производительности между горизонтальной и вертикальной поляризацией. Например средние волны вещательные станции обычно используют вертикальную поляризацию, поскольку распространение поверхностной волны над землей значительно лучше, используя вертикальную поляризацию, в то время как горизонтальная поляризация показывает незначительное улучшение для длинных сообщений расстояния, используя ионосферу. Круговая поляризация иногда используется для спутниковой радиосвязи, поскольку есть некоторые преимущества с точки зрения распространения и в преодолении замирание вызвало, если спутник меняет свою ориентацию.

Предыдущая:Что такое IPTV технологии?

Далее:Как создать свой собственный радиопередатчик

Поляризация частиц

So 8

Аналогичный эффект наблюдается при квантовомеханическом рассмотрении пучка частиц, обладающих спином. Состояние отдельной частицы в этом случае, вообще говоря, не является чистым и должно описываться соответствующей матрицей плотности. Для частицы со спином ½ (скажем, электрона) это эрмитова матрица 2×2 ρba{\displaystyle \rho _{b}^{a}} со следом 1:

ρab=ρab†=ρ¯ba{\displaystyle \rho _{ab}=\rho _{ab}^{\dagger }={\bar {\rho }}_{ba}}

trρba=1{\displaystyle \mathrm {tr} \,\rho _{b}^{a}=1}

В общем случае она имеет вид

ρba=12(δba+2σ^bas¯){\displaystyle \rho _{b}^{a}={1 \over 2}(\delta _{b}^{a}+2{\hat {\sigma }}_{b}^{a}{\bar {s}})}

Здесь σ^=(σx,σy,σz){\displaystyle {\hat {\sigma }}=(\sigma _{x},\sigma _{y},\sigma _{z})} — вектор, составленный из матриц Паули, а s¯{\displaystyle {\bar {s}}} — вектор среднего спина частицы. Величина

ρ=2|s¯|=2sx2+sy2+sz2{\displaystyle \rho =2|{\bar {s}}|=2{\sqrt {s_{x}^{2}+s_{y}^{2}+s_{z}^{2}}}}

называется степенью поляризации частицы. Это вещественное число <ρ<1.{\displaystyle 0<\rho <1.} Значение ρ=1{\displaystyle \rho =1} соответствует полностью поляризованному пучку частиц, при этом

ρba=ψa⊗ψb†{\displaystyle \rho _{b}^{a}=\psi ^{a}\otimes \psi _{b}^{\dagger }}

где ψ{\displaystyle \psi } — вектор состояния частицы. Фактически, полностью поляризованные частицы можно полностью описать вектором состояния.

Практическое значение

Левое изображение снято без фильтра, правое — через поляризационный фильтр

Скорость распространения волны может зависеть от её поляризации.

Две волны, линейно поляризованные под прямым углом друг к другу, не интерферируют.

Чаще всего это явление используется для создания различных оптических эффектов, а также в 3D-кинематографе (технология IMAX), где поляризация используется для разделения изображений, предназначенных правому и левому глазу.

Круговая поляризация применяется в антеннах космических линий связи, так как для приёма сигнала не важно положение плоскости поляризации передающей и приёмной антенн. То есть вращение космического аппарата не повлияет на возможность связи с ним

Направление вращения круговой поляризации космической приемо-передающей антенны должно совпадать с направлением вращения наземной приемо-передающей антенны, работающей с космической. То-же самое с антеннами линейной поляризации. В космической связи используется поляризационная развязка, то есть на одной частоте работают антенны противоположных направлений вращения поляризации или ортогональные с линейной поляризацией.

Антенну круговой поляризации выполнить сложнее, чем антенну линейной поляризации, для этого нужен поляризатор. Антенну с поляризацией правого направления вращения легко переделать в левого направления вращения. Для это надо всего-навсего повернуть на 90 градусов относительно оси вращения её поляризатор. Вообще, круговая поляризация — вещь теоретическая. На практике говорят об антеннах эллиптической поляризации — с левым или правым направлением вращения.

Круговая поляризация света используется также в технологиях стереокинематографа RealD и MasterImage. Эти технологии подобны IMAX с той разницей, что круговая поляризация вместо линейной позволяет сохранять стереоэффект и избегать двоения изображения при небольших боковых наклонах головы.

Поляризация волн находит применение в поляризационной голографии

История[править]

В 1669 г. датский учёный Эразм Бартолин сообщил о своих опытах с кристаллами известкового шпата (CaCO₃), чаще всего имеющими форму правильного ромбоэдра, которые привозили возвращающиеся из Исландии моряки. Он обнаружил, что луч света при прохождении сквозь кристалл расщепляется на два луча (называемых теперь обыкновенным и необыкновенным). Бартолин провёл тщательные исследования обнаруженного им явления двойного лучепреломления, однако объяснения ему дать не смог.

Спустя двадцать лет после опытов Э

Бартолина, его открытие привлекло внимание нидерландского учёного Христиана Гюйгенса, который начал исследовать свойства кристаллов исландского шпата и дал объяснение явлению двойного лучепреломления на основе своей волновой теории света

При этом он ввёл важное понятие оптической оси кристалла, при вращении вокруг которой отсутствует анизотропия свойств кристалла, то есть их зависимость от направления (такой осью обладают не все кристаллы).
В своих опытах Гюйгенс в развитие открыий Бартолина, он пропускал оба луча, вышедшие из кристалла исландского шпата, сквозь второй такой же кристалл. Оказалось, что если оптические оси обоих кристаллов параллельны, то дальнейшего разложения этих лучей уже не происходит

Если же второй ромбоэдр повернуть на 180 градусов вокруг направления распространения обыкновенного луча, то при прохождении через второй кристалл необыкновенный луч претерпевает сдвиг в направлении, противоположном сдвигу в первом кристалле, и из такой системы оба луча выйдут соединёнными в один пучок. Выяснилось также, что в зависимости от величины угла между оптическими осями кристаллов изменяется интенсивность обыкновенного и необыкновенного лучей.

Оказалось, что если оптические оси обоих кристаллов параллельны, то дальнейшего разложения этих лучей уже не происходит. Если же второй ромбоэдр повернуть на 180 градусов вокруг направления распространения обыкновенного луча, то при прохождении через второй кристалл необыкновенный луч претерпевает сдвиг в направлении, противоположном сдвигу в первом кристалле, и из такой системы оба луча выйдут соединёнными в один пучок. Выяснилось также, что в зависимости от величины угла между оптическими осями кристаллов изменяется интенсивность обыкновенного и необыкновенного лучей.

Эти исследования вплотную подвели Гюйгенса к открытию явления поляризации света, однако решающего шага он сделать не смог, поскольку световые волны в его теории предполагались продольными. Для объяснения опытов Х. Гюйгенса И. Ньютон, придерживавшийся корпускулярной теории света, выдвинул идею об отсутствии осевой симметрии светового луча и этим сделал важный шаг к пониманию поляризации света.

В 1808 г. французский физик Этьен Луи Малюс, глядя сквозь кусок исландского шпата на блестевшие в лучах заходящего солнца окна Люксембургского дворца в Париже, к своему удивлению заметил, что при определённом положении кристалла было видно только одно изображение. На основании этого и других опытов и опираясь на корпускулярную теорию света Ньютона, он предположил, что корпускулы в солнечном свете ориентированы беспорядочно, но после отражения от какой-либо поверхности или прохождения сквозь анизотропный кристалл они приобретают определённую ориентацию. Такой «упорядоченный» свет он назвал поляризованным.

Плоская спутниковая антенна

Голландский учёный Марселем Бургвал
(Marcel van de Burgwal) разработал микрочип, функционирующий
как фазирующее устройство для антенных
решеток.

Принцип работы антенны основан
на использовании программного обеспечения
для фазирования сигнала в
антенне. Современные технологии позволяют
установить её вместо параболических
антенн.

В качестве плоских спуниковых атенн
используют антенную решетку, позволяющую
электронным способом отслеживать
положение спутника на орбите.

ЗАКЛЮЧЕНИЕ

Антенна
является одним из важнейших элементов
любой радиотехнической системы, связанной
с излучением или приемом радиоволн.
К таким системам относят: системы радиосвязи,
радиовещания, телевидения, радиоуправления,
радиорелейной связи, радиолокации, радиоастрономии,
радионавигации и др. Конструктивно антенны
в процессе развития существенно видоизменялись.
Наряду с проволочными вибраторными антеннами,
созданными на первых этапах развития,
широко распространены антенны апертурные,
бегущей волны, фазированные антенные
решетки, антенны с обработкой сигнала
и др. Разработаны щелевые, импедансные,
диэлектрические, ферритовые, печатные
и другие типы конструктивного исполнения
антенн.

Кроме излучения
и приема электромагнитных волн для
передачи информации на расстояние антенная
система стала выполнять дополнительные
функции: определение угловых координат
источников излучения (с возможно большей
точностью и разрешающей способностью);
усиление сигналов, пространственную,
временную, пространственно-временную
обработку принятых сигналов, адаптацию,
самонастройку для обеспечения
помехозащищенности и электромагнитной
совместимости. В ряде случаев антенна
должна решать задачи получения внекоординатной
информации об отражающем объекте, распознавания
образа или осуществления радиовидения
путем поляризационной обработки
и голографических методов преобразования
приходящих электромагнитных полей
радиодиапазона. В некоторых антенных
задачах возникает необходимость
получения пространственно-временной
фильтрации «полей источников, расположенных
в зоне Френеля. Прорабатывается
ряд новых областей использования
антенной техники. Например, для решения
энергетических проблем предлагаются
антенные систем передачи мощности
на сверхдальние расстояния и орбитальные
солнечные станции с активными
антенными решетками для. канализации
энергии на землю. Огромную роль играет
антенная техника в решении проблем космического
оружия.

Таким образом,
наряду с антеннами, представляющими
простые взаимные устройства, применяются
активные электрически управляемые
антенные системы с присущими
им характеристиками управления, динамического
диапазона, нелинейностью, быстродействием,
гиротропией и т. д. Расчет и проектирование
таких современных антенн базируется
не только на прикладной электродинамике,
но и на теории радиотехнических систем
и сигналов, электронных цепей, технической
кибернетики и т. д. Реализуемость
требуемых антенных характеристик
во многом определяется существующей
технологической и элементной базой,
материалами, активными приборами,
фазовращателями и микропроцессорной
техникой.

СПИСОК ИСПОЛЬЗУЕМОЙ
ЛИТЕРАТУРЫ

1. Айзенберг,
Г.З. Антенны УКВ / Г.З. Айзенберг, В.Г. Ямпольский,
О.Н. Терёшин; под ред.Г.З. Айзенберга. В
2 ч. Ч.1. − М.: Связь, 2004. − 382 с.

2. Айзенберг,
Г.З. Антенны УКВ / Г.З. Айзенберг, В.Г. Ямпольский,
О.Н. Терёшин; под. ред. Г З. Айзенберга.
В 2 ч. Ч2. − М.: Связь, 2004. – 388 с.

3. Богомолов
А. Ф., Попереченко Б. А., Соколов А. Г. Следящий
параболический радиотелескоп ТНА-1500
диаметром 64 м: Антенны/Под ред. А. А. Пистолькорса.
-2002. — № 30.- 13 с.

4. Геруни П. М.
Вопросы расчета сферических двухзеркальных
антенн//Ра-диотехника и электроника. —
2004. —Т. IX, № 1, 12 с.

5. Соколов
А. Г. Металлические конструкции антенных
устройств. — М.: Стройиздат. 2008.- 240 с.

Виды поляризации

Отличие волн с круговой и плоской поляризацией

Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору с точностью до движения пространства. Волновой вектор показывает направление распространения волны, а вектор амплитуды показывает, в какую сторону происходят колебания. В трёхмерном пространстве имеется ещё одна степень свободы — возможность вращения вектора амплитуды вокруг волнового вектора. Тройка векторов, сопоставленная каждой точке бирегулярной кривой образует репер Френе.

Причиной возникновения поляризации волн может быть:

несимметричная генерация волн в источнике возмущения;
анизотропность среды распространения волн;
преломление и отражение на границе двух сред.

Поляризация описывается фигурами Лиссажу, и соответствует сложению поперечных колебаний равной частоты (с различным сдвигом фаз). При равенстве частоты колебаний фигуры Лиссажу представляют собой эллипс, двумя крайними формами которого являются круг и отрезок прямой.

В общем случае для гармонических волн конец вектора колеблющейся величины описывает в плоскости, поперечной направлению распространения волны, эллипс: это . Важными частными случаями являются линейная поляризация, при которой колебания возмущения происходят в какой-то одной плоскости, в таком случае говорят о «плоско-поляризованной волне», и круговая поляризация или циркулярная поляризация, при которой конец вектора амплитуды описывает окружность в плоскости колебаний; круговая поляризация (как и эллиптическая) в зависимости от направления вращения вектора может быть положительной или правой и отрицательной или левой.

Зависимость мгновенных потенциалов при круговой поляризации

Параметры Стокса[править]

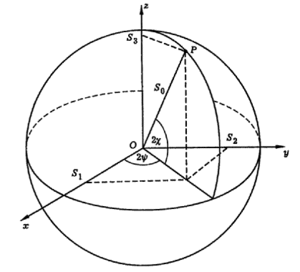
Изображение поляризации языком параметров Стокса на сфере Пуанкаре

В общем случае плоская монохроматическая волна имеет правую или левую эллиптическую поляризацию. Полная характеристика эллипса даётся тремя параметрами, например, полудлинами сторон прямоугольника, в который вписан эллипс поляризации $A_1$, $A_2$ и разностью фаз $\phi$, либо полуосями эллипса $a$, $b$ и углом $\psi$ между осью $x$ и большой осью эллипса. Удобно описывать эллиптически поляризованную волну на основе параметров Стокса:
$$S_0=A^2_1+A^2_2,$$ $S_1=A^2_1-A^2_2$,
$$~S_2=2A_1 A_2 \cos \phi,$$ $~S_2=2A_1 A_2 \sin \phi$.

Независимыми являются только три из них, ибо справедливо тождество:
$$S^2_0=S^2_1+S^2_2+S^2_3.$$

Если ввести вспомогательный угол $\chi$ , определяемый выражением $\chi=\pm a/b$ (знак $~+$ соответствует правой, а $~-$ — левой поляризации), то можно получить следующие выражения для параметров Стокса:
$$~S_1=S_0 \cos (2\chi) \cos (2\psi),$$
$$~S_2=S_0 \cos (2\chi) \sin (2\psi),$$
$$~S_3=S_0 \sin (2\chi).$$

На основе этих формул можно характеризовать поляризацию световой волны наглядным геометрическим способом. При этом параметры Стокса $~S_1$, $~S_2$, $~S_3$ интерпретируются, как декартовы координаты точки, лежащей на поверхности сферы радиуса $~S_0$. Углы $~2\chi$ и $~2\psi$ имеют смысл сферических угловых координат этой точки. Такое геометрическое представление предложил Пуанкаре, поэтому эта сфера называется сферой Пуанкаре.

Наряду с $~S_1$, $~S_2$, $~S_3$ используют также нормированные параметры Стокса $~s_1=S_1/S_0$, $~s_2=S_2/S_0$, $~s_3=S_3/S_0$. Для поляризованного света $~s^2_1+s^2_2+s^2_3=1$.

Практическое значение

Левое изображение снято без фильтра, правое — через поляризационный фильтр

Скорость распространения волны может зависеть от её поляризации.

Две волны, линейно поляризованные под прямым углом друг к другу, не интерферируют.

Поляризация волн находит применение в поляризационной голографии

Поляризация частиц

ρab=ρab†=ρ¯ba{\displaystyle \rho _{ab}=\rho _{ab}^{\dagger }={\bar {\rho }}_{ba}}

trρba=1{\displaystyle \mathrm {tr} \,\rho _{b}^{a}=1}

В общем случае она имеет вид

ρba=12(δba+2σ^bas¯){\displaystyle \rho _{b}^{a}={1 \over 2}(\delta _{b}^{a}+2{\hat {\sigma }}_{b}^{a}{\bar {s}})}

ρ=2|s¯|=2sx2+sy2+sz2{\displaystyle \rho =2|{\bar {s}}|=2{\sqrt {s_{x}^{2}+s_{y}^{2}+s_{z}^{2}}}}

ρba=ψa⊗ψb†{\displaystyle \rho _{b}^{a}=\psi ^{a}\otimes \psi _{b}^{\dagger }}

Векторы и матрицы Джонса[править | править код]

В зависимости от направления поляризации света векторы Джонса могут принимать разный вид. В частности, выделяются следующие векторы Джонса для линейной поляризации:

J→=(1){\displaystyle {\vec {J}}={\begin{pmatrix}1\\0\end{pmatrix}}} при горизонтальной поляризации;
J→=(1){\displaystyle {\vec {J}}={\begin{pmatrix}0\\1\end{pmatrix}}} при вертикальной поляризации;
J→=12(1){\displaystyle {\vec {J}}={1 \over {\sqrt {2}}}{\begin{pmatrix}1\\0\end{pmatrix}}} при поляризации под углом +45°;
J→=12(1){\displaystyle {\vec {J}}={1 \over {\sqrt {2}}}{\begin{pmatrix}0\\1\end{pmatrix}}} при поляризации под углом -45°.

Разным оптическим элементам соответствуют следующие матрицы Джонса:

(1){\displaystyle {\begin{pmatrix}1&0\\0&0\end{pmatrix}}} для горизонтального линейного поляризатора;
(1){\displaystyle {\begin{pmatrix}0&0\\0&1\end{pmatrix}}} для вертикального линейного поляризатора;
12(1111){\displaystyle {1 \over 2}{\begin{pmatrix}1&1\\1&1\end{pmatrix}}} для линейного поляризатора под углом +45°;
12(1−1−11){\displaystyle {1 \over 2}{\begin{pmatrix}1&-1\\-1&1\end{pmatrix}}} для линейного поляризатора под углом -45°.

Линейная поляризация

Линейная поляризация обусловливает существование таких известных оптических явлений, как отражение и преломление света.

Отражение волны в случае произвольной поляризации.

Линейная поляризация отраженной волны получается также при угле падения, равном углу полного преломления. В этом случае в отраженной волне вертикальная составляющая напряженности поля отсутствует и волна поляризована всегда горизонтально.

Линейную поляризацию часто называют плоской, подчеркивая этим, что колебания вектора Е осуществляются в заданной плоскости, проходящей через направление распространения волны.

Линейную поляризацию электромагнитных волн легко продемонстрировать простыми опытами в микроволновом диапазоне. Источник ( клистронный генератор) через волновод прямоугольного сечения с присоединенным к нему пирамидальным рупором ( рис. 1.3) излучает электромагнитную волну линейной поляризации.

V линейные поляризации совпадающих или взаимно перпендикулярных направлении, круговые поляризации одинакового или разных знаков. В первых двух случаях ех и е2 вещественны, причем exe2l или е О.

При линейной поляризации плоскость, содержащая луч и вектор Е, называется плоскостью колебаний, или плоскостью поляризации волны.

Кроме линейной поляризации имеются круговая и эллиптическая. При круговой поляризации конец вектора напряженности с началом на луче при перемещении по лучу в фиксированный момент времени описывает винтовую линию на круглом цилиндре, осью которого является луч, а при эллиптической — винтовую линию на эллиптическом цилиндре, причем луч проходит через центры эллиптических сечений цилиндра ( не через фокусы эллипсов в сечении. В фиксированной точке пространства на луче при линейной поляризации конец вектора & колеблется по гармоническому закону по линии колебаний, при круговой и эллиптической поляризации конец вектора & описывает соответственно окружность и эллипс с центром на луче в плоскости, перпендикулярной лучу. Круговая и эллиптическая поляризация бывают правой и левой в зависимости от направления движения конца вектора вокруг луча. С помощью принципа суперпозиции для напряженности электрического поля волну с круговой или эллиптической поляризацией можно представить в виде суперпозиции двух линейно поляризованных волн с взаимно перпендикулярными направлениями поляризациия. Поэтому при анализе поляризации электромагнитных волн достаточно ограничиться линейной поляризацией.

При линейной поляризации вектор электрического поля сохраняет свое направление вдоль определенной прямой.

Исследования линейной поляризации распределенного космического радиоизлучения в настоящее время весьма интенсивно ведутся в СССР, Нидерландах, Австралии, Великобритании и США, главным образом с целью изучения структуры галактического магнитного поля и распределения ионизированного межзвездного газа.

В случае линейной поляризации это означает перпендикулярность их направлений, а в случае круговых поляризаций — противоположность направлений вращения.

В случае линейной поляризации это означает параллельность их направлений, а в случае круговых поляризаций — снова противоположность направлений вращения.

При использовании линейной поляризации в некоторых диапазонах волн имеет место эффект Фарадея ( вращение плоскости поляризации) при прохождении волны через ионосферу. Пос-скольку величина угла поворота плоскости поляризации непостоянна и не может быть заранее определена, линейно поляризованная волна, вернувшаяся после отражения от цели к радиолокационной антенне, может иметь поляризацию, перпендикулярную излученной, в результате оказывается невозможным обнаружение цели. Волны с круговой поляризацией, несмотря на разную величину поворота компонент поля вследствие эффекта Фарадея, сохраняют поляризацию, близкую к круговой, обеспечивая уверенное слежение за целью.

В случае линейной поляризации различают поляризацию горизонтальную и вертикальную в зависимости от ориентации электрического вектора относительно поверхности земли.

Волны обеих возможных линейных поляризаций проходят через поляризатор лишь частично, с различным ослаблением.