Дешифраторы. виды двоичных дешифраторов

Прямой код

Прямой код используется в двух вариантах.В первом (основной) — для записи только неотрицательных чисел:

В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 — от 0 до 255)

Второй вариант — для записи как положительных, так и отрицательных чисел.В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).При этом, если: — знаковый разряд равен 0, то число положительное — знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:

Подводя итоги вопроса, не влезая в его дебри, скажу одно:Прямой код используется главным образом для представления неотрицательных чисел. Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):

История двоичного кода

Современная система двоичного числа, основание для двоичного кода, была обнаружена Готтфридом Лейбницем в 1679 и появляется в его статье Explication de l’Arithmétique Binaire. Полное название переведено на английский язык как «Объяснение двоичной арифметики», которая использует только знаки 1 и 0 с некоторыми замечаниями по ее полноценности, и по свету это бросает на древние китайские фигуры Фу Си». (1703). Система Лейбница использует 0 и 1, как современная система двоичной цифры. Лейбниц столкнулся со мной Чинг через французского Иезуита Джоакима Бувета и отметил с восхищением, как его hexagrams соответствуют двоичным числам от 0 до 111111 и пришли к заключению, что это отображение было доказательствами основных китайских выполнений в виде философской математики, которой он восхитился. Лейбниц рассмотрел hexagrams как подтверждение универсальности его собственных религиозных верований.

Двоичные цифры были главными в богословии Лейбница. Он полагал, что двоичные числа были символическими относительно христианской идеи creatio исключая nihilo или созданием ни из чего. Лейбниц пытался найти систему, которая преобразовывает словесные заявления логики в чистое математическое. После того, как его идеи были проигнорированы, он столкнулся с классическим китайским текстом, названным мной Чинг или ‘Книга Изменений’, которые использовали тип двоичного кода. Книга подтвердила его теорию, что жизнь могла быть упрощена или уменьшена вниз до серии прямых суждений. Он создал систему, состоящую из рядов нолей и. В это время период, Leibiniz еще не нашел использование для этой системы.

Двоичные системы счисления, предшествующие Лейбницу также, существовали в древнем мире. Вышеупомянутое я Чинг, что Лейбниц столкнулся с датами с 9-го века до н.э в Китае. Двоичная система счисления меня Чинг, текст для предсказания, основана на дуальности иня и яна. Барабаны разреза с двойными тонами используются, чтобы закодировать сообщения через Африку и Азию. Индийский ученый Пингала (вокруг 5-го – 2-е века до н.э) развил двоичную систему счисления для описания просодии в его Chandashutram.

До 1450 жители острова Мангарева во Французской Полинезии использовали гибридную двойную десятичную систему счисления. В 11-м веке ученый и философ Шао Ён развили метод для подготовки hexagrams, который переписывается, хотя неумышленно, к последовательности от 0 до 63, столь же представленный в наборе из двух предметов, с инем как 0, ян как 1 и наименее значительный бит на вершине. Заказ — также лексикографический порядок на sextuples элементов, выбранных из набора с двумя элементами.

В 1605 Фрэнсис Бэкон обсудил систему, посредством чего буквы алфавита могли быть уменьшены до последовательностей двоичных цифр, которые могли тогда быть закодированы как едва видимые изменения в шрифте в любом случайном тексте. Значительно для общей теории двойного кодирования, он добавил, что этот метод мог использоваться с любыми объектами вообще: «если те объекты быть способным к двойному различию только; как Колоколами, Трубами, Огнями и Факелами, согласно сообщению о Мушкетах и любым инструментам подобной природы».

Другой математик и философ именем Джорджа Буля опубликовали работу в 1847, названную ‘Математический Анализ Логики’, которая описывает алгебраическую систему логики, теперь известной как Булева алгебра. Система Буля была основана на наборе из двух предметов, да — нет, релейный подход, который состоял три самых основных операции: И, ИЛИ, и НЕТ. Эта система не была помещена в использование, пока аспирант от Массачусетского технологического института именем Клода Шеннона не заметил, что Булева алгебра, которую он изучил, была подобна электрической цепи. Шеннон написал свой тезис в 1937, который осуществил его результаты. Тезис Шеннона стал отправной точкой для использования двоичного кода в практическом применении, таком как компьютеры, электрические цепи, и больше.

Дополнительный код

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).

Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

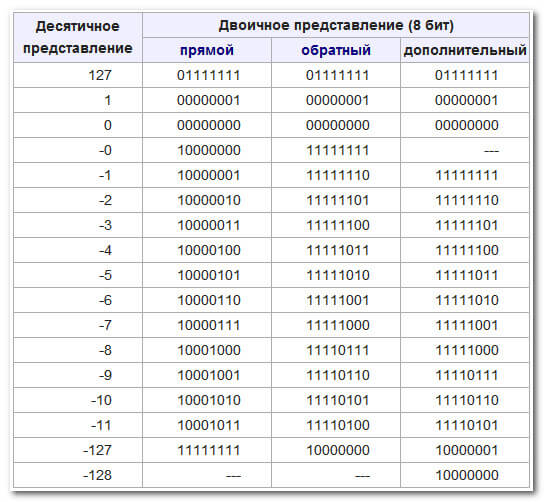
Дополнительный код отрицательного числа можно получить двумя способами1-й способ:
— инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
— к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:1111 0101 + 1 = 1111 0110 — десятичное число -10 в дополнительном коде

2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 =000 1010
Вычитаем из нуля:
0 — 0000 1010 = 1111 0110 — десятичное число -10 в дополнительном коде

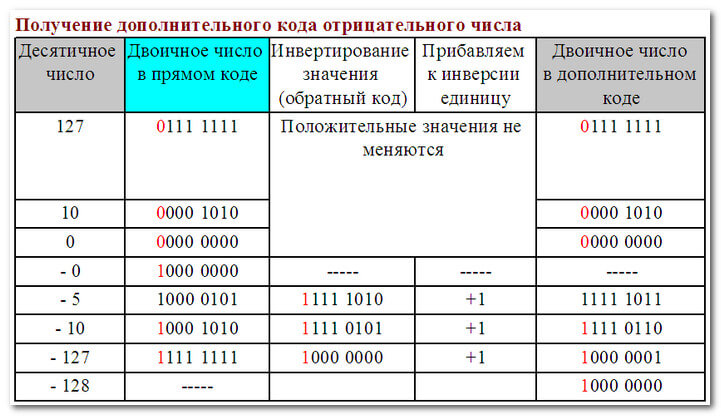
Арифметические операции с отрицательными числами в дополнительном коде

Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде

Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.

Вывод:1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода 2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода

Предыдущие статьи:1. Микроконтроллеры — первый шаг2. Системы счисления: десятичная, двоичная и шестнадцатиричная3. Логические операции, логические выражения, логические элементы4. Битовые операции

Прямой, обратный, дополнительный код двоичного числаPublished by: Мир микроконтроллеров

Date Published: 04/15/2015

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

1024

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два.
Точка, которая стоит после 1, называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, дано двоичное число 110001₂. Для перевода в десятичное запишите его как сумму по разрядам следующим образом:

То же самое чуть иначе:

Можно записать это в виде таблицы следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	1
				+32	+16	+0	+0	+0	+1

Двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.
Таким образом, двоичное число 110001₂ равнозначно десятичному 49₁₀.

Преобразование дробных двоичных чисел в десятичные

Нужно перевести число 1011010,101₂ в десятичную систему. Запишем это число следующим образом:

То же самое чуть иначе:

Или по таблице:

64	32	16	8	4	2	1		0.5	0.25	0.125
1	1	1	1	,	1	1
+64	+0	+16	+8	+0	+2	+0		+0.5	+0	+0.125

Преобразование методом Горнера

Основная статья: Метод Горнера

Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Методом Горнера обычно переводят из двоичной в десятичную систему. Обратная операция затруднительна, так как требует навыков сложения и умножения в двоичной системе счисления.

Например, двоичное число 1011011₂ переводится в десятичную систему так:

То есть в десятичной системе это число будет записано как 91.

Перевод дробной части чисел методом Горнера

Цифры берутся из числа справа налево и делятся на основу системы счисления (2).

Например 0,1101₂

Ответ: 0,1101₂= 0,8125₁₀

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. То есть нижняя цифра (1) будет самой левой и т. д. В результате получаем число 19 в двоичной записи: 10011.

Преобразование дробных десятичных чисел в двоичные

Если в исходном числе есть целая часть, то она преобразуется отдельно от дробной. Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

• Дробь умножается на основание двоичной системы счисления (2);
• В полученном произведении выделяется целая часть, которая принимается в качестве старшего разряда числа в двоичной системе счисления;
• Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются над дробной частью произведения.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам. Дробную часть 0,116 умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

Таким образом 0,116₁₀ ≈ 0,0001110110₂

Получим: 206,116₁₀ ≈ 11001110,0001110110₂

Об этой статье

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 31 человек(а). Количество просмотров этой статьи: 35 133.

Категории: Математика

English:Read Binary

Français:lire en binaire

Español:leer un código binario

Deutsch:Einen Binärcode lesen

Português:Ler Códigos Binários

Italiano:Leggere i Numeri In Sistema Binario

Bahasa Indonesia:Membaca Biner

Nederlands:Binaire getallen lezen

中文:看懂二进制

ไทย:อ่านเลขฐานสอง

العربية:قراءة سلاسل الأرقام الثنائية

한국어:이진수 읽는 법

日本語:2進数を計算する

Tiếng Việt:Giải mã số nhị phân

हिन्दी:बाइनरी नंबर पढ़ें (Read Binary)

Türkçe:İkili Sayılar Nasıl Okunur

Печать

Десятичный дешифратор

Рассмотрим пример разработки схемы дешифратора из двоичного кода в десятичный. Десятичный код обычно отображается одним
битом на одну десятичную цифру. В десятичном коде десять цифр, поэтому для отображения одного десятичного разряда требуется
десять выходов дешифратора. Сигнал с этих выводов можно подать на . В простейшем случае над светодиодом можно просто подписать индицируемую цифру.Таблица истинности
десятичного дешифратора приведена в таблице 1.

Таблица 1. Таблица истинности десятичного дешифратора.

Входы	Выходы
8	4	2	1	1	2	3	4	5	6	7	8	9
1
1	1
1	1
1	1	1
1	1
1	1	1
1	1	1
1	1	1	1
1	1
1	1	1

Для реализации принципиальной схемы дешифратора воспользуемся
методом СДНФ, так как в его таблице истинности на каждом выходе присутствует всего одна логическая единица. В результате
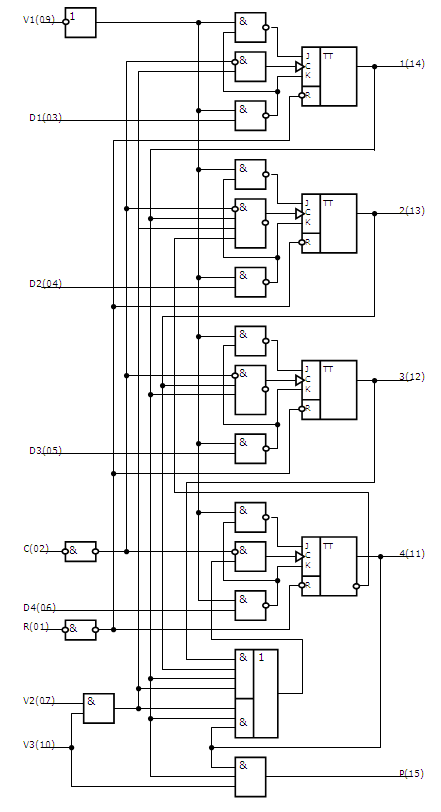
получим схему дешифратора, реализующего таблицу истинности, приведённую в таблице 1. Эта схема приведена на рисунке 1.

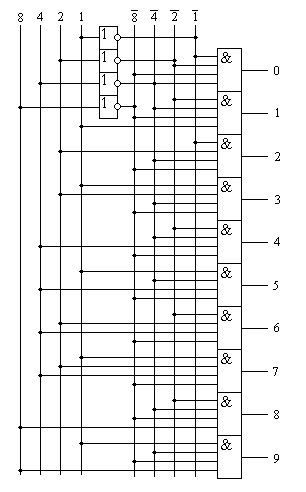
Как видно по принципиальной схеме дешифратора, для реализации каждой строки таблицы истинности потребовался логический
элемент «4И». Логические элементы «ИЛИ» не потребовались, так как в таблице истинности на каждом выходе
присутствует только одна логическая единица.

Дешифраторы выпускаются в виде отдельных микросхем или используются в составе более сложных микросхем. В настоящее
время десятичные или восьмеричные дешифраторы используются в основном как составная часть других микросхем, таких как
мультиплексоры, демультиплексоры,
ПЗУ или ОЗУ.

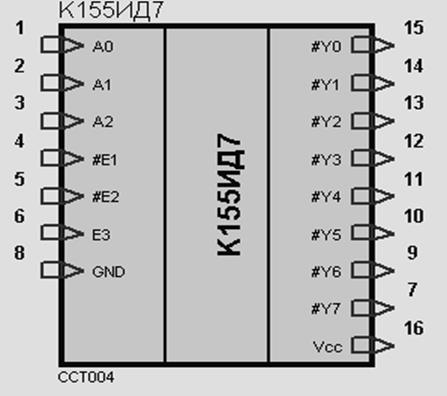
Условно-графическое обозначение микросхемы дешифратора на принципиальных
схемах приведено на рисунке 2. На этом рисунке приведено обозначение двоично-десятичного дешифратора, полная внутренняя
принципиальная схема которого изображена на рисунке 1.

Точно таким же образом можно получить принципиальную схему и для любого другого декодера (дешифратора). Наиболее
распространены схемы восьмеричных и шестнадцатеричных дешифраторов. Для индикации такие дешифраторы в настоящее
время практически не используются. В основном такие дешифраторы используются как составная часть более сложных цифровых
модулей.

Это интересно

Считается, что двоичное исчисление было изобретено в начале 18-го века математиком из Германии Готфридом Лейбницем. Однако, как недавно открыли ученые, задолго до этого аборигены полинезийского острова Мангареву использовали данный вид арифметики. Несмотря на то что колонизация практически полностью уничтожила оригинальные системы исчисления, ученые восстановили сложные двоичные и десятичные виды счета. Кроме того, ученый Когнитивист Нуньес утверждает, что кодирование двоичным кодом применялось в древнем Китае еще в 9-м веке до н. э. Другие древние цивилизации, например, индейцы майя, также использовали сложные комбинации десятичных и бинарных систем для отслеживания временных интервалов и астрономических явлений.

Бинарная кодировка в действии

Для стандартизации записи информации для компьютеров было разработано несколько кодировочных систем, одна из которых ASCII, базирующаяся на 8-и битной записи, получила широкое распространение. Значения в ней распределены особым образом:

• первый 31 символ – управляющие (с        00000000 по 00011111). Служат для служебных команд, вывода на принтер или экран, звуковых сигналов, форматирования текста;
• следующие с 32 по 127       (00100000 – 01111111) латинский алфавит и вспомогательные символы и знаки препинания;
• остальные, до 255-го           (10000000 – 11111111) –     альтернативная, часть таблицы для специальных задач и отображения национальных алфавитов;

Расшифровка значений в ней показано в таблице.

Если вы считаете, что «0» и «1» расположены в хаотичном порядке, то глубоко ошибаетесь. На примере любого числа я вам покажу закономерность и научу читать цифры, записанные двоичным кодом. Но для этого примем некоторые условности:

• Байт из 8 знаков будем читать справа налево;
• Если в обычных числах у нас используются разряды единиц, десятков, сотен, то здесь (читая в обратном порядке) для каждого бита представлены различные степени «двойки»: 256-124-64-32-16-8- 4-2-1;
• Теперь смотрим на двоичный код числа, например 00011011. Там, где в соответствующей позиции есть сигнал «1» – берем значения этого разряда и суммируем их привычным способом. Соответственно: 0+0+0+32+16+0+2+1 = 51. В правильности данного метода вы можете убедиться, взглянув на таблицу кодов.

Теперь, мои любознательные друзья, вы не только знаете что такое двоичный код, но и умеете преобразовать зашифрованную им информацию.

Логические функции двоичного дешифратора

Двоичный дешифратор работает по следующему принципу.

Пусть дешифратор имеет n входов. На входы подаётся двоичное слово xn−1xn−2…x{\displaystyle x_{n-1}x_{n-2}…x_{0}}. На выходах формируется код FF1…{\displaystyle F_{0}F_{1}…}, разрядность которого меньше или равна 2n{\displaystyle 2^{n}}. Активным становится разряд, номер которого равен численному представлению входного слова. Под активностью разряда понимается принятие им значения логической единицы, логического нуля или перевод в высокоимпедансное состояние — отключение; конкретное значение зависит от используемой реализации дешифратора. Остальные разряды остаются неактивными. Максимально возможная разрядность выходного слова равна 2n{\displaystyle 2^{n}}.

Дешифратор называется полным, если число выходов равно максимально возможной разрядности выходного слова (2n{\displaystyle 2^{n}}). Дешифратор называется неполным, если часть входных разрядов не используется (то есть число выходов меньше 2n{\displaystyle 2^{n}}).

Например, если для полного двоичного дешифратора (k=2) число входных разрядов n=3, и на вход поступает слово, состоящее из 010₂=2₁₀, на выходе будет доступно 23=8 бит, из которых активным будет только один — 2-й бит. Этот бит будет равен 1 или 0 (зависит от реализации), а остальные биты будут неактивны (либо будут равны 0 или 1, либо будут находиться в высокоимпедансном состоянии).

Функционирование одноединичного дешифратора, активные выходные сигналы которого принимают значение логической единицы, описывается системой конъюнкций:

F =x¯n−1x¯n−2…x¯1x¯{\displaystyle F_{0}\ ={\bar {x}}_{n-1}{\bar {x}}_{n-2}…{\bar {x}}_{1}{\bar {x}}_{0}}

F1 =x¯n−1x¯n−2…x¯1x{\displaystyle F_{1}\ ={\bar {x}}_{n-1}{\bar {x}}_{n-2}…{\bar {x}}_{1}x_{0}}

F2 =x¯n−1x¯n−2…x1x¯{\displaystyle F_{2}\ ={\bar {x}}_{n-1}{\bar {x}}_{n-2}…x_{1}{\bar {x}}_{0}}

…

F2n−2=xn−1xn−2…x1x¯{\displaystyle F_{{2^{n}}-2}=x_{n-1}x_{n-2}…x_{1}{\bar {x}}_{0}}

F2n−1=xn−1xn−2…x1x{\displaystyle F_{{2^{n}}-1}=x_{n-1}x_{n-2}…x_{1}x_{0}}

Часто дешифраторы дополняются входом E (от англ. enable) — «входом разрешения работы» (включения). Если на этот вход поступает активный логический сигнал (единица или ноль), то один из выходов дешифратора переходит в активное состояние, иначе все выходы неактивны вне зависимости от состояния входов.

Функционирование одноединичного дешифратора с дополнительным входом E описывается системой конъюнкций:

F =x¯n−1x¯n−2…x¯1x¯E{\displaystyle F_{0}\ ={\bar {x}}_{n-1}{\bar {x}}_{n-2}…{\bar {x}}_{1}{\bar {x}}_{0}E}

F1 =x¯n−1x¯n−2…x¯1xE{\displaystyle F_{1}\ ={\bar {x}}_{n-1}{\bar {x}}_{n-2}…{\bar {x}}_{1}x_{0}E}

F2 =x¯n−1x¯n−2…x1x¯E{\displaystyle F_{2}\ ={\bar {x}}_{n-1}{\bar {x}}_{n-2}…x_{1}{\bar {x}}_{0}E}

…

F2n−2=xn−1xn−2…x1x¯E{\displaystyle F_{{2^{n}}-2}=x_{n-1}x_{n-2}…x_{1}{\bar {x}}_{0}E}

F2n−1=xn−1xn−2…x1xE{\displaystyle F_{{2^{n}}-1}=x_{n-1}x_{n-2}…x_{1}x_{0}E}

Обычно микросхемы дешифраторов выполняют с инверсными (NOT) выходами (то есть активный выбранный разряд принимает значение логического нуля).

Двоичное слово на входе дешифратора часто называют адресом.

Беззнаковый двоичный код

Давайте разберемся, что же представляет собой такой вид записи. В целых беззнаковых кодах каждый разряд (двоичный) представляет степень цифры два. При этом наименьшее число, которое можно записать в такой форме, равно нулю, а максимальное можно представить следующей формулой: М=2п-1. Эти два числа полностью определяют диапазон ключа, которым можно выразить такой двоичный код. Давайте рассмотрим возможности упомянутой формы записи. При использовании данного вида беззнакового ключа, состоящего из восьми разрядов, диапазон возможных чисел составит от 0 до 255. Шестнадцатиразрядный код будет иметь диапазон от 0 до 65535. В восьмиразрядных процессорах для хранения и записи таких чисел используют два сектора памяти, которые располагаются в соседних адресатах. Работу с такими ключами обеспечивают специальные команды.

Язык, понятный современной технике

Конечно, алгоритм считывания двоичного кода процессорными устройствами намного сложнее. Но зато его помощью можно записать все что угодно:

• Текстовую информацию с параметрами форматирования;
• Числа и любые операции с ними;
• Графические и видео изображения;
• Звуки, в том числе и выходящие и за предел нашей слышимости;

Помимо этого, благодаря простоте «изложения» возможны различные способы записи бинарной информации:

Дырочки на перфоленте и перфокарте, соответствующие «1», были одновременно и одним из языков программирования;

Чередование ровной поверхности и выжженных впадин используется в CD и DVD дисках;

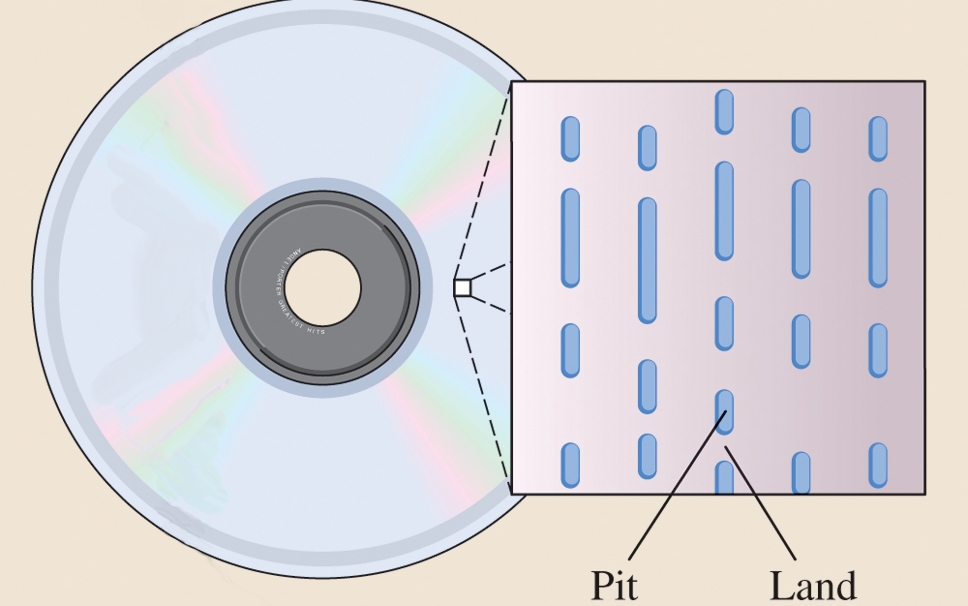
• Состоянием отдельных элементов группы транзисторов в USB накопителях;
• Изменением магнитного поля на HDD дисках;

Дополняет преимущества двоичного кодирования практически неограниченные возможности по передаче информации на любые расстояния. Именно такой способ связи используется с космическими кораблями и искусственными спутниками.

Так что, сегодня двоичная система счисления является языком, понятным большинству используемых нами электронных устройств. И что самое интересное, никакой другой альтернативы для него пока не предвидится.

Думаю, что изложенной мною информации для начала вам будет вполне достаточно. А дальше, если возникнет такая потребность, каждый сможет углубиться в самостоятельное изучение этой темы.

Я же буду прощаться и после небольшого перерыва подготовлю для вас новую статью моего блога, на какую-нибудь интересную тему.

Лучше, если вы сами ее мне подскажите 😉

Описание

Из комбинаторики известно, что, в случае непозиционного кода, количество комбинаций (кодов) n-разрядного кода является числом , равно биномиальному коэффициенту:

(n+k−1k)=(−1)k(−nk)=(n+k−1)!k!(n−1)!{\displaystyle {n+k-1 \choose k}=(-1)^{k}{-n \choose k}={\frac {\left(n+k-1\right)!}{k!\left(n-1\right)!}}}, [возможных состояний (кодов)], где:

n{\displaystyle n} — количество элементов в данном множестве различных элементов (количество возможных состояний, цифр, кодов в разряде),k{\displaystyle k} — количество элементов в наборе (количество разрядов).
В двоичной системе кодирования (n=2) количество возможных состояний (кодов) равно :

(n+k−1)!k!(n−1)!=(2+k−1)!k!(2−1)!=(k+1)!k!1!=k+1{\displaystyle {\frac {\left(n+k-1\right)!}{k!\left(n-1\right)!}}={\frac {\left(2+k-1\right)!}{k!\left(2-1\right)!}}={\frac {\left(k+1\right)!}{k!1!}}=k+1}, [возможных состояний (кодов)], то есть

описывается линейной функцией:

Nkp(k)=k+1{\displaystyle N_{kp}(k)=k+1}, [возможных состояний (кодов)], где

k{\displaystyle k} — количество двоичных разрядов.
Например, в одном 8-ми битном байте (k=8) количество возможных состояний (кодов) равно:

Nkp(k)=k+1=8+1=9{\displaystyle N_{kp}(k)=k+1=8+1=9}, [возможных состояний (кодов)].

В случае позиционного кода, число комбинаций (кодов) k-разрядного двоичного кода равно числу :

Np(k)=A¯(2,k)=A¯2k=2k{\displaystyle N_{p}(k)={\bar {A}}(2,k)={\bar {A}}_{2}^{k}=2^{k}}, где

 k{\displaystyle \ k} — число разрядов двоичного кода.

Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.

Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. Пример: в двоично-десятичном кодировании (BCD) используется двоичный код для кодирования чисел в десятичной системе счисления.
При кодировании алфавитноцифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества .

В системах счисления k-разрядный двоичный код, (k-1)-разрядный двоичный код, (k-2)-разрядный двоичный код и т. д. могут отображать одно и то же число. Например, 0001, 001, 01, 1 — одно и то же число — «1» в двоичных кодах с разным числом разрядов — k.