Разбор 2 задания егэ по информатике
Содержание:
Выполнение умножения
При практическом решении задачи умножения двух чисел необходимо свести её к последовательности более простых операций: «простое умножение», сложение, сравнение и др. Для этого разработаны различные методы умножения, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного умножения. При этом следует рассматривать умножение как процедуру (в отличие от операции).
Примерный алгоритм процедуры поразрядного умножения двух чисел
Процедура достаточно сложная, состоит из относительно большого числа шагов и при умножении больших чисел может занять продолжительное время.
Пример пошагового умножения 3 ∙ 3 = 9 на числовой прямой.
«Простое умножение» в данном контексте обозначает операцию умножения одноразрядных чисел, которая может быть легко сведена к сложению. Является гипероператором сложения:
a⋅b=hyper2(a,b)=hyper(a,2,b)=a(2)b.{\displaystyle a\cdot b=\operatorname {hyper2} (a,b)=\operatorname {hyper} (a,2,b)=a^{(2)}b.}
a(2)b=a⋅b=a+a+⋯+a⏟b.{\displaystyle a{^{(2)}}b=a\cdot b=\underbrace {a+a+\dots +a} _{b}.}
где a+a+⋯+a{\displaystyle a+a+\dots +a} — последовательное сложение b{\displaystyle b} элементов.
Чтобы упростить и ускорить процесс умножения используют табличный метод «простого умножения», для этого заранее вычисляют все комбинации произведений чисел от 0 до 9 и берут готовый результат из этой таблицы:
Таблица для умножения в десятичной системе счисления
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Данная процедура применима к умножению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.
Учим таблицу умножения на 9
Ну вот, большая часть работы сделана. Практически три четверти таблицы умножения выучены. Но, как не парадоксально, продолжать познание основ математики надо с конца, т.е. с умножения на 9.
Тут хитростей, которые облегчат ребёнку поставленную задачу, достаточно много. Самый простой способ подсчётов – на пальцах. Для этого надо поставить ладошки перед собой тыльной стороной вниз и мысленно присвоить каждому пальцу номер от 1 до 9. Чтобы, к примеру, узнать результат умножения 4 на 9 нужно загнуть палец №4 и посчитать количество не загнутых пальцев слева (десятки) и справа (единицы) от него. Получится 3 и 6, то-есть 36.
Чуть более сложный способ основан на другой закономерности. Большинство детей сразу замечают, что сумма цифр всех произведений в этом столбце равна 9, а количество десятков отличается от меняющегося множителя в меньшую сторону на единицу. Получается, что при умножении на 4 на 9 количество десятков будет 4-1=3, а количество единиц – 9-3=6, т.е. 36.
Оба эти способа запоминания одинаково хороши. Правда, ребятишки все разные и кто-то лучше осваивает таблицу умножения на 9 при помощи пальцев, а кому-то легче с математическими примерами.
Посмотрите с сыном или дочкой мультфильм.
Распределительное свойство относительно умножения
Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.
Распределительное свойство умножения относительно сложения
Умножения суммы чисел b и c на число a равносильно сумме произведений чисел a и b и a и c.
Запишем в форме буквенного выражения:
a·b+c=a·b+a·c
a, b, c — любые натуральные числа.
Теперь на наглядном примере покажем, как работает это свойство. Вычислим значение выражения 4·3+2.
4·3+2=4·3+4·2=12+8=20
С другой стороны 4·3+2=4·5=20. Справедливость распределительного свойства умножения относительно сложения показана наглядно.
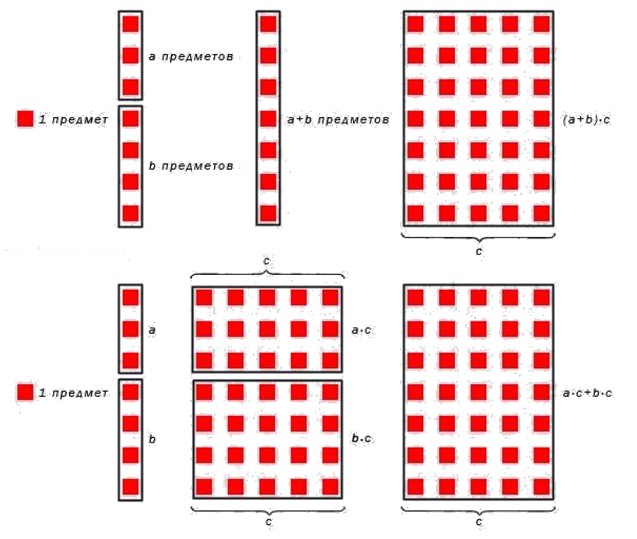
Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.
Играйте
Это будет интересно ученику. Есть ряд игр, помогающих запомнить примеры, отточить свои знания ответов на них.
- Карточки. Изготовьте карточки с примерами, но ответы на них не пишите. Их угадать ребенок должен сам. Если он правильный, карточку из общей стопки откладываем, а если нет – возвращаем. Играть можно ежедневно. За правильные решения ученика можно поощрять призами, а за неправильные – «поощрять» другими заданиями – например, уборкой, декламацией стихов и т. д.
- Игра наоборот. Напишите на карточках числа и предложите игроку самому составить под них примеры. Для некоторых ответов может быть несколько примеров. Для наглядности – для «40» подходит 4х10, 5х8.
- Жизненные примеры. Составляйте их из жизненного опыта ребенка, учитывая его интересы. Можно спросить, сколько всего колес у четырех автомобилей.
играй в таблицу умножения
Сочетательное свойство умножения натуральных чисел
Второе название для сочетательного свойства умножения — ассоциативный закон, или ассоциативное свойство. Вот его формулировка.
Сочетательный закон умножения
Умножение числа a на произведение чисел b и c равносильно умножению произведения чисел a и b на число c.
Приведем формулировку в буквенном виде:
a·b·c=a·b·c
a, b, c — любые натуральные числа. Сочетательный закон работает для трех и более натуральных чисел.
Для наглядности приведем пример. Сначала вычислим значение 4·3·2.
4·3·2=4·6=4+4+4+4+4+4=24
Теперь переставим скобки и вычислим значение 4·3·2.
4·3·2=12·2=12+12=24
4·3·2=4·3·2
Как видим, теория совпадает с практикой, и свойство справедливо.
Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.
Еще несколько вариантов занимательных игр
Можно поиграть в игру «Лото» с теми же самыми карточками-примерами. Подготовьте на бумаге поля, которые заполнены одними ответами. Вытягивая из стопки произвольно по одной карточке с примером, малыш должен положить ее в ячейку с правильным ответом.
Проведите с ребенком устную викторину. К примеру, назовите число 28 и спросите, при умножении каких чисел получается такой результат.
Обучение будет более продуктивным, если примеры из таблицы умножения одновременно использовать и на практике. Мальчику нравятся машинки, предложите ему посчитать, сколько всего колесиков у 6 машин. Каждая машинка имеет по 4 колеса, значит, это число умножаем на количество машинок. В итоге получится 24 колеса. Девочке приведите пример на двух косичках у кукол. На каждую косичку нужно по резинке. Сколько нужно резинок для 7 кукол?
Перенеситесь вместе с ребенком в мир сказок и любимых персонажей. Обыграйте различные ситуации. Представьте Карлсона, который сдувает свечи сразу с трех тортов. Сколько свечей всего на тортах? Или Красная шапочка несет бабушке гостинцы. В каждой руке по одной корзинке с пирожками. Сколько пирожков в двух корзинках?
Масса примеров находятся рядом с вами, нужно только присмотреться вокруг. От вас требуется проявить наблюдательность и фантазию, тогда ваш ребенок сможет выучить таблицу умножения не только с легкостью, но и с большим интересом.

К изучению таблицы умножения подключите для наглядности подручные материалы, например, карандаши или счетные палочки. Поставьте на стол 5 стаканов и поместите в каждый по 3 палочки – всего 15 штук. Объясните маленькому ученику, что общее число карандашей – это число карандашей в каждом стакане, умноженное на количество самих стаканов.
Разложите на столе 4 тарелки, поместите в них по 5 конфет. Предложите ребенку сосчитать общее количество конфеток.
Применение стихотворной формы – действенный метод в изучении таблицы умножения. На слух и в рифму ребенку будет легче запомнить числа. В интернете найдется большое количество стихов, которые помогут малышу выучить таблицу умножения.
Данная методика будет полезна, например, для изучения умножения на 3. С этим числом часто возникают трудности.

Вариант с загадками в стихах не менее увлекателен. Оставьте концовку стиха без ответа, ребенок догадается в рифму о каком числе идет речь.
Семь обезьянок по восемь бананов принялись съесть. Сколько бананов съели всего? 56
Игры с малышом помогут закрепить полученные знания. Если ребенок так и не понял, как устроена таблица умножения, то ожидаемого эффекта вы можете не получить.