Цифровой компаратор
Содержание:
- Компараторы с двумя и более напряжениями сравнения
- Конструкция компаратора
- Логические функции
- Таблицы истинности компаратора
- Принцип построения импульсных генераторов на ОУ
- Логические функции
- Схемотехника компараторов
- Использование[править | править код]
- Сравнение сигналовправить | править код
- Определение заполненности контейнеровправить | править код
- Определение пластинкиправить | править код
- Взаимодействие с командным блокомправить | править код
- Взаимодействие с тортомправить | править код
- Взаимодействие с котломправить | править код
- Взаимодействие с рамкойправить | править код
- Другоеправить | править код
- Особенности цифрового компаратора
Компараторы с двумя и более напряжениями сравнения
Строятся на двух и более обычных компараторах.
Двухпороговый (троичный) компаратор
Двухпороговый (троичный) компаратор имеет два напряжения сравнения и состоит из двух обычных компараторов. Два напряжения сравнения делят весь диапазон входных напряжений на три нечётких поддиапазона в нечёткой (fuzzy) троичной логике, которым присваиваются три чётких значения в чёткой троичной логике. Двухбитный троичный (2B BCT) логический сигнал (трит) на выходе троичного компаратора указывает, в каком из трёх поддиапазонов находится входное напряжение. Логическая часть троичного компаратора выполняет — «повторитель» (F1073 = F810). Двухбитный троичный трит (2B BCT) может быть преобразован в трёхбитный трит (3B BCT) или в трёхуровневый трит (3LCT).[источник не указан 267 дней]
В аналитическом виде двухпороговый (троичный) компаратор задаётся следующими системами неравенств:
- {Uref2>Uref1Uout1={,if Uin<Uref1undefined,if Uin=Uref11,if Uin>Uref1Uout2={,if Uin<Uref2undefined,if Uin=Uref21,if Uin>Uref2{\displaystyle {\begin{cases}U_{ref2}>U_{ref1}\\U_{out1}={\begin{cases}0,&{\mbox{if }}U_{in}<U_{ref1}\\undefined,&{\mbox{if }}U_{in}=U_{ref1}\\1,&{\mbox{if }}U_{in}>U_{ref1}\end{cases}}\\U_{out2}={\begin{cases}0,&{\mbox{if }}U_{in}<U_{ref2}\\undefined,&{\mbox{if }}U_{in}=U_{ref2}\\1,&{\mbox{if }}U_{in}>U_{ref2}\end{cases}}\end{cases}}}
где:
Uref1 и Uref2 — напряжения нижнего и верхнего порогов сравнения,
Uout1 и Uout2 — выходные напряжения компараторов, а
Uin — входное напряжение на компараторах.
Двухпороговый (троичный) компаратор является простейшим одноразрядным троичным АЦП.
Троичный компаратор является переходником из нечёткой (fuzzy) троичной логики в чёткую троичную логику для решения задач нечёткой троичной логики средствами чёткой троичной логики.
Тумблеры и переключатели на 3 положения без фиксации (ON)-OFF-(ON) являются механоэлектрическими троичными (двухпороговыми) компараторами, в которых входной величиной является механическое отклонение рычага от среднего положения.
Двухпороговый (троичный) компаратор выпускается в виде отдельной микросхемы MA711H (К521СА1).
Применяется в популярной микросхемы-таймера NE555.
Троичный компаратор низкого качества с двоичными компараторами на цифровых логических элементах 2И-НЕ применён в троичном индикаторе напряжения источника питания с преобразованием трёх диапазонов входного напряжения в один трёхбитный одноединичный трит (3B BCT). Для построения в этой схеме не хватает двоичного RS-триггера, который можно выполнить на двух дополнительных логических элементах 2И-НЕ (например, использовать два из четырёх логических элементов 2И-НЕ микросхемы К155ЛА3).
Многовходовые компараторы
Входной каскад параллельных АЦП прямого преобразования является многоуровневым компаратором. В нём применяются 2n−1{\displaystyle 2^{n}-1} напряжений сравнения, где n — количество битов выходного кода. Разность соседних уровней сравнения в таких многовходовых компараторах обычно постоянна.
Конструкция компаратора
КН нашли обширную область применения в радиоэлектронике разнообразной направленности. В магазинах радиотоваров можно увидеть огромное количество разнообразных микросхем. Но особенно часто применяемыми микросхемами у пользователей считаются:
- LM No 339;
- LM No 311;
- MAX No 934;
- К554СА3.
Они легкодоступны в торговой сети и имеют довольно бюджетную цену. Такие КН выделяются обширным спектром входных параметров. К выходу КН способна присоединяться разнообразная токовая нагрузка, как правило, не превосходящая 50.0 мА. Это могут быть микрореле, варистор, световой диод, оптрон либо абсолютно разные исполнительные модули, однако с предельными по току компонентами.
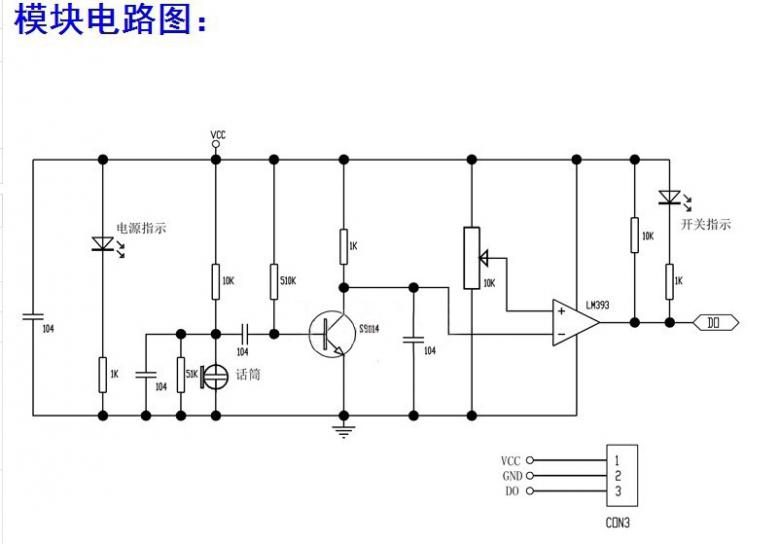
Фотореле контроля
Подобное реле выпускается методом навесного монтажа. Его применяют в охранных контролирующих системах либо для контролирования степени света. Входящее напряжение попадает на делитель R1 и фотодиод VD3. Их объединенная точка сочетания использует ограничивающие диоды VD1/ VD2, подключенные к входам DA1. В итоге входящая разность потенциалов КН будет отсутствовать, а следовательно, и восприимчивость измерителя станет максимальной.
Фотореле
Чтобы выходящий сигнал смог инвертироваться, потребуется обеспечить входную разницу в 1 мВ. По той причине, что к входу подсоединены С1 и сопротивление R1, размер U на нем станет увеличиваться с незначительной задержкой, равноправной периоду заряда С1.
Зарядный блок
Такой блок питания принимается функционировать непосредственно после сборки. Его базовые опции сводятся к установлению рабочего зарядного тока и порогов, по которым срабатывает КН. При подключении прибора зажигается световой диод, позиционирующий подачу напряжения. На протяжении процесса зарядки обязан непрерывно гореть алый световой диод, который погаснет после того, как аккумуляторная батарея будет полностью заряжена
Зарядный блок
Подводимое напряжение от питающего блока настраивается R2, а зарядный ток устанавливается с применением R4. Наладка выполняется с применением сопротивления на 160 Ом, подключающегося в параллель к контактам, которые держат батарейку. Транзистор VT1 размещается на радиаторе, взамен его можно применять КТ814Б. Подобную схему надо будет комплектовать на плате с размером не более 50×50 мм.
Кварцевый генератор
Этот генератор ортогональных импульсов выполняется с использованием российского компаратора K544C3, функционирующего на тактовой гармонике 32.768 Гц. Схема станет рабочей в спектре входящего напряжения 7-11В с частотой установленной кварцем ZQ1. Тем не менее, для эксплуатации такого девайса сверх 50.0 кГц потребуется понизить значение R5-R6.
Генератор
При замыкании другого вывода с 0-проводом КН становится подсоединённым по варианту с незакрытым коллектором, а R7 становится нагрузкой. Подстраивание частотности производится совместно, с применением C1. С применением R4 выполняется автозапуск генератора. Меняя значение R2, изменяется импульсная характеристика.
Дополнительная информация! Выбирая конденсаторы С1 или С2, генератор сможет применяться в виде бесконтактного жидкостного датчика. В роли детектора для этой цели потребуется применять микроконтроллер с ПО. Однако возможно использовать и ещё дополнительно компаратор, который станет фиксировать деформации напряжения.
Отсюда следует, что компаратор способен предназначать действия по уровням значений на собственных вводах. Когда они отличаются, то, исходя от дельты U, выход прибора меняет качественное положение. Именно такие их качества используют создатели, разрабатывая самые разные электроприборы с операционным усилителем.
Логические функции
Для примера рассмотрим два 4-х битных слова A{\displaystyle A} и B{\displaystyle B}, пусть эти слова представляют собой некоторые натуральные числа, представленные в двоичном виде, причем 3-й разряд будет старшим:
- A=A3,A2,A1,A{\displaystyle A=A_{3},A_{2},A_{1},A_{0}},
- B=B3,B2,B1,B{\displaystyle B=B_{3},B_{2},B_{1},B_{0}}
Здесь каждая буква с нижним цифровым индексом представляет один из битов в числах.
- Равенство (эквивалентность)
Двоичные числа A{\displaystyle A} и B{\displaystyle B} будут равны, если все пары соответственных битов обоих чисел равны, то есть:
- A3=B3{\displaystyle A_{3}=B_{3}}, A2=B2{\displaystyle A_{2}=B_{2}}, A1=B1{\displaystyle A_{1}=B_{1}} и A=B{\displaystyle A_{0}=B_{0}}.
В двоичной записи чисел их цифры это или 0, или 1. Булева функция для равенства любых двух цифр Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} (здесь логическая операция «ИЛИ» обозначена символом +{\displaystyle +}, а «И» символом точки) может быть выражена как:
- xi=Ai⋅Bi+A¯i⋅B¯i{\displaystyle x_{i}=A_{i}\cdot B_{i}+{\overline {A}}_{i}\cdot {\overline {B}}_{i}}.
При этом xi{\displaystyle x_{i}} равна 1 только если Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} равны.
Для равенства Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}}, все функции xi{\displaystyle x_{i}} (для i = 0, 1, 2, 3) должны быть равны 1.
Поэтому признак равенства Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} записывается в виде логической функции как
- (A=B)=x3⋅x2⋅x1⋅x{\displaystyle \ (A=B)=x_{3}\cdot x_{2}\cdot x_{1}\cdot x_{0}}.
Двоичная функция (A=B){\displaystyle (A=B)} равна 1 только если все пары цифр двух чисел равны.
- Неравенство (неэквивалентность)
Чтобы определить наибольшее из двух двоичных чисел, мы рассмотрим отношение величин пар значащих цифр, начиная со старших битов к младшим битам до нахождения неравенства в некоторой позиции. Когда неравенство найдено, то, если соответствующий бит A{\displaystyle A} равен 1 и такой же бит B{\displaystyle B} равен 0, то мы считаем, что A>B{\displaystyle A>B}.
Это последовательное сравнение может быть выражено логическими выражениями как:
- (A>B)=A3⋅B¯3+x3⋅A2⋅B¯2+x3⋅x2⋅A1⋅B¯1+x3⋅x2⋅x1⋅A⋅B¯{\displaystyle (A>B)=A_{3}\cdot {\overline {B}}_{3}+x_{3}\cdot A_{2}\cdot {\overline {B}}_{2}+x_{3}\cdot x_{2}\cdot A_{1}\cdot {\overline {B}}_{1}+x_{3}\cdot x_{2}\cdot x_{1}\cdot A_{0}\cdot {\overline {B}}_{0}},
- (A<B)=A¯3⋅B3+x3⋅A¯2⋅B2+x3⋅x2⋅A¯1⋅B1+x3⋅x2⋅x1⋅A¯⋅B{\displaystyle (A<B)={\overline {A}}_{3}\cdot B_{3}+x_{3}\cdot {\overline {A}}_{2}\cdot B_{2}+x_{3}\cdot x_{2}\cdot {\overline {A}}_{1}\cdot B_{1}+x_{3}\cdot x_{2}\cdot x_{1}\cdot {\overline {A}}_{0}\cdot B_{0}}.
(A>B){\displaystyle (A>B)} и (A<B){\displaystyle (A<B)} — выходные двоичные переменные, которые равны 1 когда A>B{\displaystyle A>B} или A<B{\displaystyle A<B} соответственно.
Таблицы истинности компаратора
Для примеров приведены таблицы истинности тривиального однобитового и двухбитового компараторов.
Логическая функция однобитового цифрового компаратора описывается таблицей истинности:
| Входы | Выходы | |||
|---|---|---|---|---|
| A{\displaystyle A} | B{\displaystyle B} | A<B{\displaystyle A<B} | A=B{\displaystyle A=B} | A>B{\displaystyle A>B} |
| 1 | ||||
| 1 | 1 | |||
| 1 | 1 | |||
| 1 | 1 | 1 |
Таблица истинности двухбитового компаратора:
| Входы | Выходы | |||||
|---|---|---|---|---|---|---|
| A1{\displaystyle A_{1}} | A{\displaystyle A_{0}} | B1{\displaystyle B_{1}} | B{\displaystyle B_{0}} | A<B{\displaystyle A<B} | A=B{\displaystyle A=B} | A>B{\displaystyle A>B} |
| 1 | ||||||
| 1 | 1 | |||||
| 1 | 1 | |||||
| 1 | 1 | 1 | ||||
| 1 | 1 | |||||
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | |||
| 1 | 1 | |||||
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | |||
| 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | 1 |
Принцип построения импульсных генераторов на ОУ
В предыдущих статьях я рассказывал об импульсных генераторах с различной формой импульсов, выполненных на транзисторах. Для простых устройств их, возможно, применять, но для создания сложных устройств с регулировкой различных параметров их схемы оказываются неоправданно трудоёмкими в настройке и разработке. Поэтому для упрощения схемотехнической реализации применяют генераторы импульсов в основе, которых лежат операционные усилители.
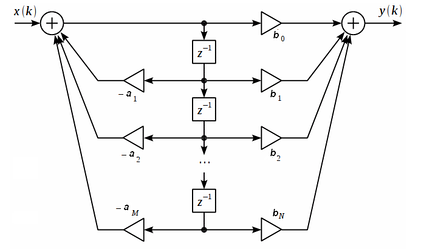
В общем случае для получения импульсов различной формы требуется замкнутая система, которая состоит из трёх основных частей: интегратора, компаратора и логической схемы.
Блок-схема генератора колебаний различной формы.
Хотя схема состоит из трех частей, но довольно часто в простых генераторах применяют один-два операционных усилителя. Для повышения гибкости и универсальности схем генераторов можно добавлять дополнительные ОУ.
Первой рассматриваемым генератором будет мультивибратор, то есть генератор прямоугольных импульсов.
Логические функции
Для примера рассмотрим два 4-х битных слова A{\displaystyle A} и B{\displaystyle B}, пусть эти слова представляют собой некоторые натуральные числа, представленные в двоичном виде, причем 3-й разряд будет старшим:
- A=A3,A2,A1,A{\displaystyle A=A_{3},A_{2},A_{1},A_{0}},
- B=B3,B2,B1,B{\displaystyle B=B_{3},B_{2},B_{1},B_{0}}
Здесь каждая буква с нижним цифровым индексом представляет один из битов в числах.
- Равенство (эквивалентность)
Двоичные числа A{\displaystyle A} и B{\displaystyle B} будут равны, если все пары соответственных битов обоих чисел равны, то есть:
- A3=B3{\displaystyle A_{3}=B_{3}}, A2=B2{\displaystyle A_{2}=B_{2}}, A1=B1{\displaystyle A_{1}=B_{1}} и A=B{\displaystyle A_{0}=B_{0}}.
В двоичной записи чисел их цифры это или 0, или 1. Булева функция для равенства любых двух цифр Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} (здесь логическая операция «ИЛИ» обозначена символом +{\displaystyle +}, а «И» символом точки) может быть выражена как:
- xi=Ai⋅Bi+A¯i⋅B¯i{\displaystyle x_{i}=A_{i}\cdot B_{i}+{\overline {A}}_{i}\cdot {\overline {B}}_{i}}.
При этом xi{\displaystyle x_{i}} равна 1 только если Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} равны.
Для равенства Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}}, все функции xi{\displaystyle x_{i}} (для i = 0, 1, 2, 3) должны быть равны 1.
Поэтому признак равенства Ai{\displaystyle A_{i}} и Bi{\displaystyle B_{i}} записывается в виде логической функции как
- (A=B)=x3⋅x2⋅x1⋅x{\displaystyle \ (A=B)=x_{3}\cdot x_{2}\cdot x_{1}\cdot x_{0}}.
Двоичная функция (A=B){\displaystyle (A=B)} равна 1 только если все пары цифр двух чисел равны.
- Неравенство (неэквивалентность)
Чтобы определить наибольшее из двух двоичных чисел, мы рассмотрим отношение величин пар значащих цифр, начиная со старших битов к младшим битам до нахождения неравенства в некоторой позиции. Когда неравенство найдено, то, если соответствующий бит A{\displaystyle A} равен 1 и такой же бит B{\displaystyle B} равен 0, то мы считаем, что A>B{\displaystyle A>B}.
Это последовательное сравнение может быть выражено логическими выражениями как:
- (A>B)=A3⋅B¯3+x3⋅A2⋅B¯2+x3⋅x2⋅A1⋅B¯1+x3⋅x2⋅x1⋅A⋅B¯{\displaystyle (A>B)=A_{3}\cdot {\overline {B}}_{3}+x_{3}\cdot A_{2}\cdot {\overline {B}}_{2}+x_{3}\cdot x_{2}\cdot A_{1}\cdot {\overline {B}}_{1}+x_{3}\cdot x_{2}\cdot x_{1}\cdot A_{0}\cdot {\overline {B}}_{0}},
- (A<B)=A¯3⋅B3+x3⋅A¯2⋅B2+x3⋅x2⋅A¯1⋅B1+x3⋅x2⋅x1⋅A¯⋅B{\displaystyle (A<B)={\overline {A}}_{3}\cdot B_{3}+x_{3}\cdot {\overline {A}}_{2}\cdot B_{2}+x_{3}\cdot x_{2}\cdot {\overline {A}}_{1}\cdot B_{1}+x_{3}\cdot x_{2}\cdot x_{1}\cdot {\overline {A}}_{0}\cdot B_{0}}.
(A>B){\displaystyle (A>B)} и (A<B){\displaystyle (A<B)} — выходные двоичные переменные, которые равны 1 когда A>B{\displaystyle A>B} или A<B{\displaystyle A<B} соответственно.
Схемотехника компараторов
Схемотехнически простейший компаратор представляет собой дифференциальный усилитель с высоким коэффициентом усиления (в идеале — бесконечным). Обычно в качестве компараторов напряжения в современной электронике применяют микросхемы операционных усилителей (ОУ). Но существуют и выпускаются специализированные для применения в качестве компараторов микросхемы.
Микросхема компаратора отличается от обычного линейного (ОУ) устройством и входного, и выходного каскадов:
Входной каскад компаратора должен выдерживать широкий диапазон дифференциальных входных напряжений (между инвертирующим и неинвертирующим входами), вплоть до значений питающих напряжений, а также полный диапазон синфазных напряжений.
Выходной каскад компаратора обычно конструируют совместимым по логическим уровням и токам с распространённым типом входов логических схем (технологий ТТЛ, ЭСЛ и т. п.). Возможны исполнения выходного каскада компаратора на одиночном транзисторе с , что обеспечивает одновременную совместимость с ТТЛ и КМОП логическими микросхемами.
Микросхемы компараторов не рассчитаны для работы с отрицательной обратной связью как ОУ и при их применении отрицательная обратная связь не используется. И наоборот, для формирования гистерезисной передаточной характеристики компараторы часто охватывают положительной обратной связью
Эта мера позволяет избежать быстрых нежелательных переключений состояния выхода, обусловленном шумами во входном сигнале, при медленно изменяющемся входном сигнале.
При проектировании микросхем компараторов уделяется особое внимание быстрому восстановлению входного каскада после перегрузки и смены знака разности входных напряжений. В быстродействующих компараторах для повышения быстродействия схемотехнически не допускают захода биполярных транзисторов в выходном каскаде в режим насыщения.
Компараторы охваченные положительной обратной связью имеют гистерезис и по сути являются двухпороговыми компараторами, часто такой компаратор называют триггером Шмитта.
При равенстве входных напряжений реальные компараторы и ОУ, включенные по схеме компараторов дают хаотически изменяющийся выходной сигнал из-за собственных шумов и шумов входных сигналов. Обычная мера подавления такого хаотического переключения — введение положительной обратной связи для получения гистерезисной передаточной характеристики.
При программном моделировании компаратора возникает проблема выходного напряжения компаратора при одинаковых напряжениях на обоих входах компаратора. В этой точке компаратор находится в состоянии неустойчивого равновесия. Проблему можно решить множеством разных способов, описанных в подразделе «программный компаратор».
Программное моделирование компаратора
В программах в качестве первого приближения можно использовать простейшую модель асимметричного компаратора, в котором третье значение с равными величинами сравниваемых входных переменных постоянно приписывается к «0» или к «1», в примере, приведенном ниже, третье значение постоянно приписывается к «0»:
DEFINT Y DEFSNG X Xref=2.5 Xin=2.6 IF Xin>Xref THEN Y=1 ELSE Y=0 'Асимметричный компаратор PRINT Y
В более сложных моделях симметричных компараторов третье значение можно, в рамках двоичной логики:
- приписать к «0» или к «1» постоянно,
- приписывать к «0» или к «1» случайным образом динамически,
- учитывать предыдущее значение и считать равенство недостаточным для переключения,
- учитывать первую производную и её равенство нулю считать недостаточным для переключения,
или выйти за рамки двоичной логики и:
- для учёта третьего значения (равенство) применить соответствующую троичную функцию из чёткой троичной логики с чётким третьим значением.
Существующая проблема третьего состояния при программном моделировании, когда два числа, представленные кодовыми словами, могут быть в точности равны, на практике не имеет места: два напряжения не могут в точности совпадать, так как, во-первых, аналоговое напряжение величина неквантуемая, а во-вторых, существует шум, напряжение смещения входов компаратора, и иные возмущения, разрешающие неоднозначность даже в случае равенства входных напряжений аналогового компаратора.
Использование[править | править код]
Сравнение сигналовправить | править код
Компаратор имеет два входа: один сзади (сигнал А) и один сбоку (сигнал Б). Если к обеим боковым сторонам подведен сигнал, сигналом Б считается более сильный из них. Существует два режима вывода, переключаемые щелчком правой кнопки мыши на компараторе.
- В первом режиме (факел спереди не горит, режим по умолчанию) компаратор сравнивает сигнал А с сигналом Б и пропускает сигнал А только если А≥Б. Если А слабее Б, на выходе будет ноль.
- Во втором режиме (факел спереди горит) компаратор «вычитает» сигнал Б из сигнала А, выдавая на выход сигнал с силой, равной разности входов (А−Б).
Определение заполненности контейнеровправить | править код
Компаратор, у задней стороны которого находится контейнер, позволяет снимать с него сигнал, зависящий от заполненности хранилища. Доступные контейнеры включают в себя: обычные и двойные сундуки и сундуки-ловушки, печи, варочные стойки, раздатчики, выбрасыватели, загрузочные воронки и нажимные рельсы с вагонеткой с сундуком или воронкой на них. При этом можно размещать компаратор через 1 полный блок, но только если компаратор находится на одной линии с контейнером. Если контейнер пуст, на выходе будет ноль. Если контейнер содержит что-либо, выходной сигнал рассчитывается по следующей формуле:
| A | = | 1 | + | ( | N1 V1 | + | N2 V2 | + | … | + | Nn Vn | ) | × | 14 n |
| Где: | ||
| A | — | сила сигнала (С округлением в меньшую сторону) |
| N1…n | — | количество предметов в слоте |
| V1…n | — | размер полной стопки для данного предмета |
| n | — | количество слотов в контейнере |
Это означает, что сила сигнала зависит не напрямую от количества предметов в контейнере, а от его заполненности. Так, предмет, который нельзя сложить в стопку, полная стопка предметов, складывающихся по 16 предметов, и полная стопка предметов, складывающихся по 64 предмета, занимают одинаковый объём и на выходе дают одинаковый сигнал (например, раздатчик с 9 вагонетками выдаст максимальный сигнал — 15).
Определение пластинкиправить | править код
Компаратор, подключённый входом к проигрывателю, в котором находится пластинка, дает сигнал с силой, зависящей от порядкового номера используемой пластинки.
| Сигнал | Пластинка |
|---|---|
| нет | |
| 1 | 13 |
| 2 | cat |
| 3 | blocks |
| 4 | chirp |
| 5 | far |
| 6 | mall |
| 7 | mellohi |
| 8 | stal |
| 9 | strad |
| 10 | ward |
| 11 | 11 |
| 12 | wait |
| 13 | не используется |
| 14 | не используется |
| 15 | не используется |
Взаимодействие с командным блокомправить | править код
Если компаратор подключён входом к командному блоку, в котором введена команда , при обновлении командного блока будет выдаваться сигнал, соответствующий количеству сущностей на сервере, соответствующих аргументу команды.
Если же в командном блоке введена любая другая команда, при её успешном выполнении будет выдаваться сигнал силой 1.
Взаимодействие с тортомправить | править код
Если компаратор подключён входом к торту, он будет выдавать сигнал, пропорциональный количеству оставшегося торта. Каждый кусок торта добавляет 2 к силе выходного сигнала. Таким образом, полный торт выдаёт через компаратор сигнал силы 14.
Взаимодействие с котломправить | править код
Если компаратор подключён входом к котлу, он будет выдавать сигнал, пропорциональный количеству воды в котле. Пустой котёл выдаёт сигнал силы 0. Каждая треть воды в котле добавляет 1 к выходному сигналу.
Взаимодействие с рамкойправить | править код
Компаратор может быть использован для определения угла поворота предмета в рамке, а также определения того, содержится ли там какой-либо предмет вообще. Чтобы считывать сигнал с рамки, компаратор должен быть подключен к блоку, на котором висит рамка, с противоположной от неё стороне. Пустая рамка выдаёт нулевой сигнал. Неповёрнутый предмет в рамке выдаёт сигнал силы 1. Каждые 45° поворота добавляют 1 к силе выходного сигнала.
Другоеправить | править код
- Компаратор пропускает сигнал только в одну сторону, а потому может быть использован как диод. Но в отличие от повторителя, компаратор не усиливает сигнал.
- Если поставить два компаратора в кольцо, потом подать и снять сигнал с этого кольца, то сигнал будет плавно затухать со скоростью длина провода минус 1 за 0,1 секунды (для каждого участка). Это позволяет сделать более компактную линию поддержки сигнала, чем на повторителях.
- Компаратор, подключённый к рамке портала Края, выдаёт сигнал силы 15, если в рамке расположено око Края, и 0, если рамка пуста.
- Задержка компаратора равна 0,1 секунды или двум тактам.
Особенности цифрового компаратора
Цифровой компаратор – это однобитный аналогово-цифровой преобразователь.
Напряжение выхода представляет либо логический «0», либо «1».
На вход может быть подан как аналоговый, так и цифровой сигнал.
Устройство используется в качестве формирователя импульсов для сопряжения схем датчиков и устройств отображения.
Может применяться для анализа спектра звукового или светового сигнала.
Компаратор – это также логические элементы «или» и «не», используемые в вычислительной технике.
Теоретически при незначительно малых колебаниях уровня входного сигнала, может возникать состояние неопределенности выхода. На практике равенство измеряемого и опорного напряжений не наступает. Поскольку компаратор имеет ограниченный коэффициент усиления или положительную обратную связь.