Индуктивность. генри. henry. гн. единицы измерения. доли, миллигенри, мгн, микрогенри, мкгн. соотношения. формулы
Введение
Если бы кому-нибудь пришла в голову идея провести опрос населения Земли на тему «Что вы знаете об индуктивности?», то подавляющее число опрашиваемых просто пожало бы плечами. А ведь это второй по многочисленности вслед за транзисторами технический элемент, на котором зиждется современная цивилизация! Любители детективов, припомнив, что в своей юности зачитывались захватывающими рассказами сэра Артура Конан Дойла о приключениях знаменитого сыщика Шерлока Холмса, с разной степенью уверенности пробормочут что-то о методе, которым вышеозначенный сыщик пользовался. При этом подразумевая метод дедукции, который, наравне с методом индукции, является основным методом познания в западной философии Нового времени.
При методе индукции происходит исследование отдельных фактов, принципов и формирование общих теоретических концепций на основе полученных результатов (от частного к общему). Метод дедукции, наоборот, предполагает исследование от общих принципов, законов, когда положения теории распределяются на отдельные явления.
Следует отметить, что индукция, в смысле метода, не имеет сколько-нибудь прямого отношения к индуктивности, просто они имеют общий латинский корень inductio — наведение, побуждение — и обозначают совершенно разные понятия.
Лишь малая часть опрашиваемых из числа носителей точных наук — профессиональных физиков, инженеров-электротехников, радиоинженеров и студентов этих направлений — смогут дать внятный ответ на этот вопрос, а некоторые из них готовы прочитать с ходу целую лекцию на эту тему.
Определение индуктивности
В физике индуктивность, или коэффициент самоиндукции, определяется как коэффициент пропорциональности L между магнитным потоком Ф вокруг проводника с током и порождающим его током I или — в более строгой формулировке — это коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током:
или
Для понимания физической роли катушки индуктивности в электрических цепях можно использовать аналогию формулы энергии, запасаемой в ней при протекании тока I, с формулой механической кинетической энергии тела.
При заданной силе тока I индуктивность L определяет энергию магнитного поля W, создаваемого этим током I:
Аналогично, механическая кинетическая энергия тела определяется массой тела m и его скоростью V:
То есть индуктивность, подобно массе, не позволяет энергии магнитного поля мгновенно увеличиться, равно как и масса не позволяет проделать такое с кинетической энергией тела.
Проведём исследование поведения тока в индуктивности:
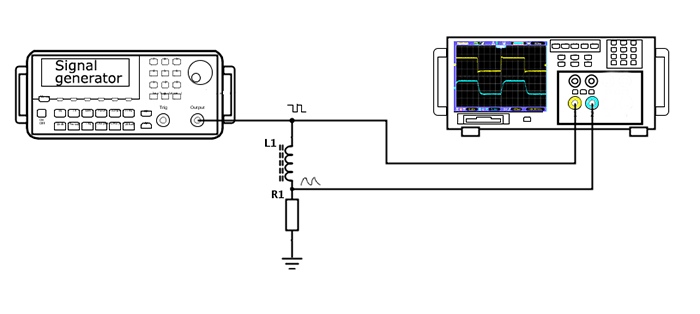 Рис. 1. Электрическая схема эксперимента
Рис. 1. Электрическая схема эксперимента
Рис. 2. Физическая реализация эксперимента
Рис. 3. Осциллограмма тока через индуктивность. Желтая осциллограмма — выход сигнал-генератора, голубая — сигнал на резисторе.
Из-за инерционности индуктивности происходит затягивание фронтов входного напряжения. Такая цепь в автоматике и радиотехнике называется интегрирующей, и применяется для выполнения математической операции интегрирования.
Проведём исследование напряжения на катушке индуктивности:
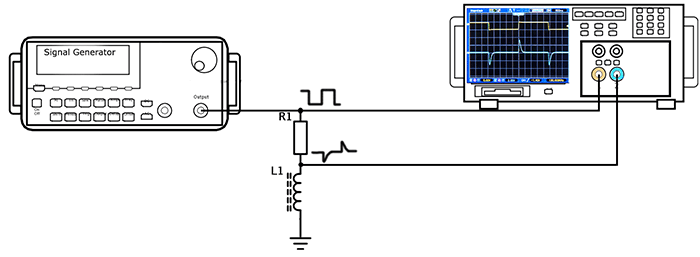 Рис. 4. Электрическая схема эксперимента
Рис. 4. Электрическая схема эксперимента
Рис. 6. Осциллограмма напряжения на индуктивности (голубая)
В моменты подачи и снятия напряжения из-за присущей катушкам индуктивности ЭДС самоиндукции, возникают выбросы напряжения. Такая цепь в автоматике и радиотехнике называется дифференцирующей, и применяется в автоматике для корректировки процессов в управляемом объекте, носящих быстрый характер.
Рис. 5. По большому счёту, во всех генераторах электрического тока любого типа, равно как и в электродвигателях, их обмотки представляют собой катушки индуктивности.
Кратные и дольные единицы генри:
Кратные и дольные единицы образуются с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Гн | декагенри | даГн | daH | 10−1 Гн | децигенри | дГн | dH |
| 102 Гн | гектогенри | гГн | hH | 10−2 Гн | сантигенри | сГн | cH |
| 103 Гн | килогенри | кГн | kH | 10−3 Гн | миллигенри | мГн | mH |
| 106 Гн | мегагенри | МГн | MH | 10−6 Гн | микрогенри | мкГн | µH |
| 109 Гн | гигагенри | ГГн | GH | 10−9 Гн | наногенри | нГн | nH |
| 1012 Гн | терагенри | ТГн | TH | 10−12 Гн | пикогенри | пГн | pH |
| 1015 Гн | петагенри | ПГн | PH | 10−15 Гн | фемтогенри | фГн | fH |
| 1018 Гн | эксагенри | ЭГн | EH | 10−18 Гн | аттогенри | аГн | aH |
| 1021 Гн | зеттагенри | ЗГн | ZH | 10−21 Гн | зептогенри | зГн | zH |
| 1024 Гн | иоттагенри | ИГн | YH | 10−24 Гн | иоктогенри | иГн | yH |
Примечание: Фото https://www.pexels.com, https://pixabay.com
Как возможно научиться писать тексты и зарабатывать на этом удаленно? Например, можете пройти курс «Копирайтинг от А до Я», который подойдет даже начинающим авторам.
Другие записи:
карта сайта
1 генри единица измерения индуктивности магнитного потока физика формула перевод единиц единицей измерения какой физической величины является 1 генриединицей си магнитного потока является генри гн
Коэффициент востребованности
1 328
Историческая справка
Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz), который известен своим вкладом в изучение электромагнетизма, и который вывел правило Ленца о свойствах индукционного тока. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry), который открыл самоиндукцию. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
В числе учёных, принявших участие в исследованиях свойств индуктивности и разработке различных её применений, необходимо упомянуть сэра Генри Кавендиша, который проводил эксперименты с электричеством; Майкла Фарадея, который открыл электромагнитную индукцию; Николу Тесла, который известен своей работой над системами передачи электричества; Андре-Мари Ампера, которого считают первооткрывателем теории об электромагнетизме; Густава Роберта Кирхгофа, который исследовал электрические цепи; Джеймса Кларка Максвелла, который исследовал электромагнитные поля и частные их примеры: электричество, магнетизм и оптику; Генри Рудольфа Герца, который доказал, что электромагнитные волны действительно существуют; Альберта Абрахама Майкельсона и Роберта Эндрюса Милликена. Конечно, все эти ученые исследовали и другие проблемы, о которых здесь не упоминается.
Катушка индуктивности
По определению, катушка индуктивности — это винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Как следствие, при протекании через катушку переменного электрического тока, наблюдается его значительная инерционность, которую можно наблюдать в описанном выше эксперименте. В высокочастотной технике катушка индуктивности может состоять из одного витка или его части, в предельном случае на сверхвысоких частотах для создания индуктивности используется отрезок проводника, который обладает так называемой распределённой индуктивностью (полосковые линии).
Опыты
В заключение хотелось бы рассказать о некоторых любопытных свойствах катушек индуктивности, которые вы могли бы сами понаблюдать, имея под рукой простейшие материалы и доступные приборы. Для проведения опытов нам потребуется отрезки изолированного медного провода, ферритовый стержень и любой современный мультиметр с функцией измерения индуктивности. Вспомним, что любой проводник с током создаёт вокруг себя магнитное поле такого вида, показанное на рисунке 7.
 Рис. 8. Магнитное поле катушки с током.
Рис. 8. Магнитное поле катушки с током.
Намотаем на ферритовый стержень четыре десятка витков провода с небольшим шагом (расстоянием между витками). Это будет катушка №1. Затем намотаем такое же количество витков с таким же шагом, но с обратным направлением намотки. Это будет катушка №2. И затем намотаем 20 витков в произвольном направлении вплотную. Это будет катушка №3. Затем аккуратно снимем их с ферритового стержня. Магнитное поле таких катушек индуктивности выглядит примерно так, кака показано на рис. 8.
Рис. 10.
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. На рисунке 8 показана катушка с немагнитным сердечником, роль немагнитного сердечника исполняет воздух. На рис. 9 показаны примеры катушек индуктивности с магнитным сердечником, который может быть замкнутым или разомкнутым.
Рис. 11.
В основном используют сердечники из феррита и пластин из электротехнической стали. Сердечники повышают индуктивность катушек в разы. В отличие от сердечников в форме цилиндра, сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, так как магнитный поток в них замкнут.
Рис. 12.
Подключим концы мультиметра, включенного в режим измерения индуктивности, к концам катушки №1. Индуктивность такой катушки чрезвычайно мала, порядка нескольких долей микрогенри, поэтому прибор ничего не показывает (рис. 10). Начнём вводить в катушку ферритовый стержень (рис. 11). Прибор показывает порядка десятка микрогенри, причем при продвижении катушки к центру стержня её индуктивность возрастает примерно в три раза (рис. 12).
Рис. 13.
По мере продвижения катушки к другому краю стержня, значение индуктивности катушки опять падает. Вывод: индуктивность катушек может регулироваться путем перемещения в них сердечника, и максимальное её значение достигается при расположении катушки на ферритовом стержне (или, наоборот, стержня в катушке) в центре. Вот мы и получили настоящий, пусть и несколько неуклюжий, вариометр. Проделав вышеописанный опыт с катушкой №2, мы получим аналогичные результаты, то есть направление намотки на индуктивность не влияет.
Рис. 14.
Уложим витки катушки №1 или №2 на ферритовом стержне поплотнее, без зазоров между витками, и снова измерим индуктивность. Она увеличилась (рис. 13).
Рис. 15.
А при растягивании катушки по стержню её индуктивность уменьшается (рис. 14). Вывод: изменяя расстояние между витками можно подстраивать индуктивность, а для максимальной индуктивности наматывать катушку надо «виток к витку». Приёмом подстройки индуктивности путём растягивания или сжатия витков частенько пользуются радиотехники, настраивая свою приёмопередающую аппаратуру на нужную частоту.
Установим на ферритовый стержень катушку №3 и измерим её индуктивность (рис. 15). Число витков уменьшилось в два раза, а индуктивность уменьшилась в четыре раза. Вывод: чем меньше количество витков — тем меньше индуктивность, и нет линейной зависимости между индуктивностью и числом витков.
Автор статьи: Sergey Akishkin