Арктангенс, арккотангенс

Вычисление значения арктангенса

Арктангенс является тригонометрическим выражением. Он исчисляется в виде угла в радианах, тангенс которого равен числу аргумента арктангенса.

Для вычисления данного значения в Экселе используется оператор ATAN, который входит в группу математических функций. Единственным его аргументом является число или ссылка на ячейку, в которой содержится числовое выражение. Синтаксис принимает следующую форму:

Способ 1: ручной ввод функции

Для опытного пользователя, ввиду простоты синтаксиса данной функции, легче и быстрее всего произвести её ручной ввод.

1. Выделяем ячейку, в которой должен находиться результат расчета, и записываем формулу типа:

   Вместо аргумента «Число», естественно, подставляем конкретное числовое значение. Так арктангенс четырех будет вычисляться по следующей формуле:

   Если числовое значение находится в какой-то определенной ячейке, то аргументом функции может служить её адрес.

Для вывода результатов расчета на экран нажимаем на кнопку Enter.

Способ 2: вычисление при помощи Мастера функций

Но для тех пользователей, которые ещё не полностью овладели приемами ручного ввода формул или просто привыкли с ними работать исключительно через графический интерфейс, больше подойдет выполнение расчета с помощью Мастера функций.

1. Выделяем ячейку для вывода результата обработки данных. Жмем на кнопку «Вставить функцию», размещенную слева от строки формул.

Происходит открытие Мастера функций. В категории «Математические» или «Полный алфавитный перечень» следует найти наименование «ATAN». Для запуска окна аргументов выделяем его и жмем на кнопку «OK».

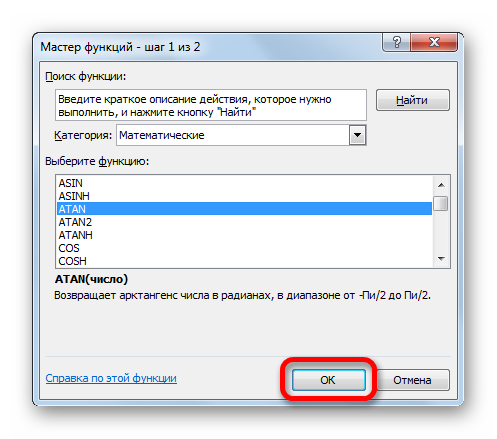
После выполнения указанных действий откроется окно аргументов оператора. В нем имеется только одно поле – «Число». В него нужно ввести то число, арктангенс которого следует рассчитать. После этого жмем на кнопку «OK».

Также в качестве аргумента можно использовать ссылку на ячейку, в которой находится это число. В этом случае проще не вводить координаты вручную, а установить курсор в область поля и просто выделить на листе тот элемент, в котором расположено нужное значение. После этих действий адрес этой ячейки отобразится в окне аргументов. Затем, как и в предыдущем варианте, жмем на кнопку «OK».

После выполнения действий по вышеуказанному алгоритму в предварительно обозначенной ячейке отобразится значение арктангенса в радианах того числа, которое было задано в функции.

Урок: Мастер функций в Excel

Как видим, нахождение из числа арктангенса в Экселе не является проблемой. Это можно сделать с помощью специального оператора ATAN с довольно простым синтаксисом. Использовать данную формулу можно как путем ручного ввода, так и через интерфейс Мастера функций.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Нахождение значения arcsin через arccos, arctg, arcctg и т.п.

Задача нахождения значения арксинуса числа через известный арккосинус этого числа, арккосинуса через известный арксинус, арктангенса через арккотангенс и арккотангенса через известный арктангенс решается очень просто – достаточно использовать формулы arcsin a+arccos a=π/2 и arctg a+arcctg a=π/2 (смотрите ).

Например, пусть нам известно, что arcsin a=−π/12, а нужно найти значение arccos a. Вычисляем нужное нам значение арккосинуса: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12.

Куда интереснее обстоит дело, когда по известному значению арксинуса или арккосинуса числа a требуется найти значение арктангенса или арккотангенса этого числа a или наоборот. Формул, задающих такие связи, мы, к сожалению, не знаем. Как же быть? Разберемся с этим на примере.

Пусть нам известно, что арккосинус числа a равен π/10, и нужно вычислить значение арктангенса этого числа a. Решить поставленную задачу можно так: по известному значению арккосинуса найти число a, после чего найти арктангенс этого числа. Для этого нам сначала потребуется таблица косинусов, а затем – таблица тангенсов.

Угол π/10 радиан – это угол 18 градусов, по таблице косинусов находим, что косинус 18 градусов приближенно равен 0,9511, тогда число a в нашем примере есть 0,9511.

Осталось обратиться к таблице тангенсов, и с ее помощью найти нужное нам значение арктангенса 0,9511, оно приближенно равно 43 градусам 34 минутам.

Эту тему логически продолжает материал статьи вычисление значений выражений, содержащих arcsin, arccos, arctg и arcctg.

Список литературы.

• Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
• Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
• Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
• И. В. Бойков, Л. Д. Романова. Сборникк задач для подготовки к ЕГЭ, часть 1, Пенза 2003.
• Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2

Значения арксинуса, арккосинуса, арктангенса и арккотангенса

Сначала стоит разобраться, что вообще такое «значение арксинуса, арккосинуса, арктангенса и арккотангенса».

Для этого обратимся к . Если под арксинусом, арккосинусом, арктангенсом и арккотангенсом числа a понимать угол, то значением арксинуса, арккосинуса, арктангенса и арккотангенса числа a логично считать величину этого угла. Если под арксинусом, арккосинусом, арктангенсом и арккотангенсом числа a понимать число, то оно и является значением соответствующей аркфункции.

Чтобы окончательно все стало понятно, приведем пример.

Например, по определению арккосинуса угол (число) π/3 является арккосинусом одной второй, так как этот угол (число) лежит в рамках от нуля до пи, и косинус этого угла (числа) равен 1/2. Таким образом, значение арккосинуса одной второй есть угол пи на три радианов (число пи на три). При этом говорят: «Арккосинус одной второй равен пи на три». На письме подобные выражения записывают в виде равенства, рассматриваемому примеру соответствует запись arccos(1/2)=π/3. Заметим, что величина угла может быть указана и в градусах. Так как угол π/3 рад равен углу 60 градусов (смотрите перевод градусов в радианы и обратно), то для нашего примера значением арккосинуса 1/2 можно указать угол 60 градусов, то есть, .

Inverse cosine graph

A function f has an inverse function if, and only if, f is a one-to-one function. The whole cosine function is not one-to-one, since

, for every integer

What can we do then?

As stated in the previous paragraph, we need to restrict the domain of basic periodic cosine function. Thus, as cosine is always in the range , and we choose the domain, , the inverse cosine function properties will be the reverse of this:

• Inverse cosine domain of x for real result:

• Inverse cosine range of usual principal value:

In the table below you will find the inverse cosine graph, as well as some commonly used arccos values:

x	arccos(x)	Graph
	°	rad
-1	180°	π
-√3 / 2	150°	5π/6
-√2 / 2	135°	3π/4
-1/2	120°	2π/3
90°	π/2
1/2	60°	π/3
√2 / 2	45°	π/4
√3 / 2	30°	π/6
1	0°

Wondering where this inverse cosine graph comes from? It’s simply created by reflecting the graph of cos x through the line y = x (don’t forget about our domain restrictions!):

Функция arcsin

График функции y=arcsin⁡x{\displaystyle y=\arcsin x}

Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого sin⁡y=x,−π2⩽y⩽π2,|x|⩽1.{\displaystyle \sin y=x,\quad -{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}},\quad |x|\leqslant 1.}

Функция y=arcsin⁡x{\displaystyle y=\arcsin x} непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.

• sin⁡(arcsin⁡x)=x{\displaystyle \sin(\arcsin x)=x\qquad } при −1⩽x⩽1,{\displaystyle -1\leqslant x\leqslant 1,}
• arcsin⁡(sin⁡y)=y{\displaystyle \arcsin(\sin y)=y\qquad } при −π2⩽y⩽π2,{\displaystyle -{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}},}
• D(arcsin⁡x)=−1;1{\displaystyle D(\arcsin x)=\qquad } (область определения),
• E(arcsin⁡x)=−π2;π2{\displaystyle E(\arcsin x)=\left\qquad } (область значений).

Свойства функции arcsin

• arcsin⁡(−x)=−arcsin⁡x{\displaystyle \arcsin(-x)=-\arcsin x\qquad } (функция является нечётной).
• arcsin⁡x>{\displaystyle \arcsin x>0} при <x⩽1{\displaystyle 0<x\leqslant 1}.
• arcsin⁡x={\displaystyle \arcsin x=0} при x={\displaystyle x=0.}
• arcsin⁡x<{\displaystyle \arcsin x<0} при −1⩽x<{\displaystyle -1\leqslant x<0.}
• arcsin⁡x={arccos⁡1−x2,⩽x⩽1−arccos⁡1−x2,−1⩽x<{\displaystyle \arcsin x=\left\{{\begin{matrix}\arccos {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\-\arccos {\sqrt {1-x^{2}}},\qquad -1\leqslant x<0\end{matrix}}\right.}
• arcsin⁡x=arctg⁡x1−x2{\displaystyle \arcsin x=\operatorname {arctg} {\frac {x}{\sqrt {1-x^{2}}}}}
• arcsin⁡x={arcctg1−x2x,<x⩽1arcctg1−x2x−π,−1⩽x<{\displaystyle \arcsin x=\left\{{\begin{matrix}\operatorname {arcctg} \,{\frac {\sqrt {1-x^{2}}}{x}},\qquad 0<x\leqslant 1\\\operatorname {arcctg} \,{\frac {\sqrt {1-x^{2}}}{x}}-\pi ,\qquad -1\leqslant x<0\end{matrix}}\right.}

Получение функции arcsin

Дана функция y=sin⁡x.{\displaystyle y=\sin x.} На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y=arcsin⁡x{\displaystyle y=\arcsin x} функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — −π2;π2{\displaystyle \left}. Так как для функции y=sin⁡x{\displaystyle y=\sin x} на интервале −π2;π2{\displaystyle \left} каждое значение функции достигается при единственном значении аргумента, то на этом отрезке существует обратная функция y=arcsin⁡x,{\displaystyle y=\arcsin x,} график которой симметричен графику функции y=sin⁡x{\displaystyle y=\sin x} на отрезке −π2;π2{\displaystyle \left} относительно прямой y=x.{\displaystyle y=x.} (графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов координатной плоскости Oxy{\displaystyle Oxy})

Арктангенс и арккотангенс − теория, примеры и решения

Функция арктангенс и ее график

Функция тангенс определена в интервале кроме точек , … и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции тангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arctg y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арктангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арктангенс.

1. Область определения функции: .
2. Область значений функции: .
3. Функция является нечетной: .
4. Функция возрастает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

В интервале для уравнения (2) существует одно t, для которого tg t=a. Это решение

Следовательно в интервале уравнение (2) имеет один корень. Так как тангенс периодичная функция с основным периодом π, то все корни уравнения (2) отличаются на πn (n∈Z), т.е.

Решение уравнения (2) представлен на Рис.3:

Так как tg t − это ординат точки пересечения прямой OM_t1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OT_t пересекается с окружностью с радиусом 1 в двух точках: . Но только точка соответствует интервалу , которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Используя онлайн калькулятор получим:

Функция арккотангенс и ее график

Как известно, функция котангенс определена в интервале кроме точек -2π, —π 0, π, 2π,… и не является монотонной функцией (Рис.4) (подробнее о функции котангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arcctg y. Поменяв местами x и y, получим:

Функция (4) − это функция, обратная к функции

График функции арккотангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арккотангенс.

1. Область определения функции: .
2. Область значений функции: .
3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
4. Функция убывает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:

Решения уравнения (5) можно представить на единичной окружности (Рис.6):

ctg t − это абсцис точки пересечения прямой с прямым y=1. Любому числу a на линии котангенс соответствует только одна точка . Прямая пересекется с единичной окружностью в двух точках . Но только точка соответствует интервалу (0; π), которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (6):

Так как в интервале (0; π), то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (6), имеем

С помощью онлайн калькулятора вычисляем . Тогда

Inverse cosine — why should I care? Some obscure arccos applications

You may think that arccos is another useless term from trigonometry, but we want to convince you this is not the case! The inverse cosine function is really helpful for many scientific and real-life problems (awesome, isn’t it?):

I Science

Maths:

Solving the triangle, using the law of cosines. If you know the three sides of a triangle, and you’d like to find any of the triangle’s angles, you’ll need to use arccos.

Physics:

• Finding the angle between two vectors/ lines / line segments — rearrange the dot product formula so that angle is the subject of equation. And there you are, an inverse cosine application.

• Finding the hydraulic radius of a partially filled pipe is possible if you know wetted perimeter, calculated from a formula using arccos.

Chemistry:

Arccos is useful for estimating the optimal bond angles of polyatomic molecules, like e.g. H2O or CH4

II Real-life examples

• Calculating your roof pitch, or inclination angle of a staircase (though, depending on what dimensions are given, the inverse sine or inverse tangent calculators may also be handy)
• Designing a ramp for disabled people or pushchairs. Inverse cosine will be extremely useful if you know the ramp’s length and the available horizontal distance.
• ️ Even choosing an ergonomic position at work! If you want to properly set up your work station, you’ll need to know your optimal desk height or standing desk height, but, as for positioning the monitor — finding the tilt angle or viewing angle is a way easier with this arccos calculator.

Арксинус и арккосинус − теория, примеры и решения

Функция арксинус и ее график

Как известно, функция синус определена в интервале и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции синус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию синус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция sin x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arcsin y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арксинус.

1. Область определения функции: .
2. Область значений функции: .
3. Функция является нечетной: .
4. Функция возрастает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором sin x>1 (см. график функции синус (Рис.1). При |a|≤1, в отрезке (дуга DAB) уравнение (2) имеет одно решение (см. Рис.3):

В отрезке (дуга DCB) функция синус убывает и принимает значения от 1 до −1. Следовательно в этом отрезке уравнение (2) также имеет решение:

Действительно:

А из

следует

т.е.

Таким образом уравнение (3) имеет два решения в отрезке :

которые совпадают при |a|=1.

Поскольку функция синус периодичная с основным периодом 2π, имеем

Тогда получим решение (2) в виде

Решения (3) и (4) удобно представить одним уравнением:

Действительно. При четных k (k=2n) из уравнения (5) получают все решения, представленные уравнением (3), а при нечетных k (k=2n+1) − все решения, представленные уравнением (4).

При a=1, arcsin a и π−arcsin a совпадают (т.к. ), следовательно решение уравнения sin t=1 имеет вид:

При |a|=−1, из (3) и (4) следует:

Но поворот эквивалентно повороту . То есть уравнения (6) и (7) эквивалентны. Тогда решение уравнения sin t=−1 запишем в виде:

При |a|=0, из (3) и (4) имеем следующее решение уравнения sin t=0:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (5):

т.е.

Функция арккосинус и ее график

Как известно, функция косинус определена в интервале и не является монотонной функцией (Рис.4) (подробнее о функции косинус смотрите на странице Синус и косинус. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию косинус можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция cos x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arccos y. Поменяв местами x и y, получим:

Функция (8) − это функция, обратная к функции

График функции арксинус можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арксинус.

1. Область определения функции: .
2. Область значений функции: .
3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
4. Функция убывает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

При |a|>1 это уравнение не имеет решения, т.к. не существует такое число x, при котором cos x>1 (см. график функции косинус (Рис.4). При |a|≤1, в отрезке [0; π] (дуга ABC) уравнение (9) имеет одно решение t₁=arccos a. В отрезке [−π; 0] (дуга CDA) уравнение (9) имеет одно решение t₂=−arccos a(см. Рис.6):

Таким образом, в интервале [−π; π] уравнение (9) имеет два решения y=± arccos a, которые совпадают при a=1.

Поскольку функция косинус периодичная с основным периодом 2π:

то общее решение (9) имеет следующий вид:

При a=1, числа arccos a и −arccos a совпадают (они равны нулю), тогда решение уравнения cos t=1 можно записать так:

При a=−1, имеем cos t=−1,

При a=0, имеем cos t=0,

Решение тригонометрического уравнения cos t=0 можно записать одним уравнением:

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (10):

Так как , то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

Так как (), то

Пример 3. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (10), имеем

С помощью онлайн калькулятора вычисляем : . Тогда решение можно записать так:

График функции косинус (y=cos x)

Для построения графика функции косинус, поставим в соответствие любому числу α, абсциссу соответствующей точки на единичной окружности (Рис.13).

Пусть точка M движется по окружности в положительном направлении (против часовой стрелки) начиная с точки A.

Вектор радиус точки M с осью OX имеет угол α. Увеличивая этот угол от нуля до π/2 абсцисс точки M уменьшается от 1 до 0. Далее, увеличивая этот угол от π/2 до π, абсцисс точки M увеличивается от 0 до 1. Построим график функции косинус на отрезке [0,π]. Так как привычнее запись функции в виде y=cos x, то вместо cos α мы будем использовать cos x, а y− это значение функции соответствующей точке x.

В декартовой прямоугольной системе координат, на оси OX отметим точки (можно взять π≈3 и тогда этим точкам будут соответствовать числа 0, 0.5, 1, 1.5, 2, 2.5, 3). Далее, используя таблицу 1, запишем соответствующие значения y.

Построим график:

Равенство (11) показывает, что функция синус симметрична относительно оси ординат (т.е. четна). Тогда добавив построенной линии, линию, симметричную относительно оси ординат, получим:

Равентство (13)((15)) показывает, что косинус периодичная функция с периодом 2π( 360°). Это означает, что функция в диапазоне [−π;π] повторяется начиная с π направо и с −π влево:

Область определения функции косинус (−∞;+∞). Область значений: .

What is the inverse of cosine (arccos)?

Arccos is the inverse of a trigonometric function — specifically, the inverse of the cosine function. However, as trigonometric functions are periodic, then, in a strict sense, they cannot be inverted. We can deal with that problem by choosing an interval in which the basic function is monotonic. You can pick many different ranges, but for cosine the common choice is . This range is called the set of principal values.

Abbreviation	Definition	Domain of arccos x for real result	Range of usual principal values
arccos(x) cos-1x, acos	x = cos(y)	-1 ≤ x ≤ 1	0 ≤ y ≤ π 0° ≤ y ≤ 180°

Arccos(x) is the most commonly used notation, as cos-1x may be misleading — remember that inverse cosine is not the same as the reciprocal of the function (in other words, raising to the power -1):