Логические операторы (справочник по c#)boolean logical operators (c# reference)
Содержание:
3.10. Как упростить логическую формулу
Равносильные преобразования логических формул имеют то же назначение, что и
преобразования формул в обычной алгебре. Они служат для упрощения формул или
приведения их к определённому виду путем использования основных законов алгебры
логики.
| Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных. |
Некоторые преобразования логических формул похожи на преобразования формул
в обычной алгебре (вынесение общего множителя за скобки, использование
переместительного и сочетательного законов и т.п.), тогда как другие
преобразования основаны на свойствах, которыми не обладают операции обычной
алгебры (использование распределительного закона для конъюнкции, законов
поглощения, склеивания, де Моргана и др.).
Покажем на примерах некоторые приемы и способы, применяемые при упрощении
логических формул:
1) 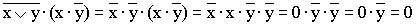 (законы алгебры логики применяются в следующей последовательности: правило
(законы алгебры логики применяются в следующей последовательности: правило
де Моргана, сочетательный закон, правило операций переменной с её инверсией и
правило операций с константами);
2) 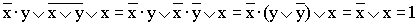 (применяется правило де Моргана, выносится за скобки общий множитель,
(применяется правило де Моргана, выносится за скобки общий множитель,
используется правило операций переменной с её инверсией);
3) 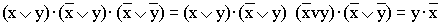 (повторяется второй сомножитель, что разрешено законом
(повторяется второй сомножитель, что разрешено законом
идемпотенции; затем комбинируются два первых и два последних сомножителя и
используется закон склеивания);
4) 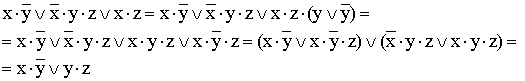 (вводится вспомогательный логический сомножитель (); затем
(вводится вспомогательный логический сомножитель (); затем
комбинируются два крайних и два средних логических слагаемых и используется
закон поглощения);
5) (сначаладобиваемся, чтобы знак отрицания стоял только перед
отдельными переменными, а не перед их комбинациями, для этого дважды применяем
правило де Моргана; затем используем закон двойного отрицания);
6) 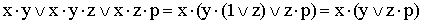 (выносятся за скобки общие множители; применяется правило операций с
(выносятся за скобки общие множители; применяется правило операций с
константами);
7) 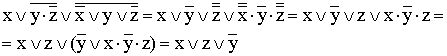 (к
(к
отрицаниям неэлементарных формул применяется правило де Моргана; используются
законы двойного отрицания и склеивания);
8) 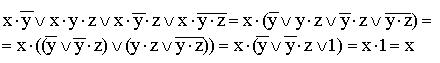 (общий множитель x выносится за скобки, комбинируются слагаемые в скобках —
(общий множитель x выносится за скобки, комбинируются слагаемые в скобках —
первое с третьим и второе с четвертым, к дизъюнкции применяется правило операции переменной с её инверсией);
9) 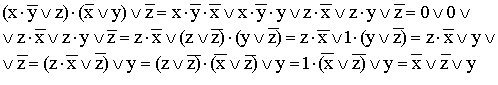 (используются распределительный закон для дизъюнкции, правило операции
(используются распределительный закон для дизъюнкции, правило операции
переменной с ее инверсией, правило операций с константами, переместительный
закон и распределительный закон для конъюнкции);
10) 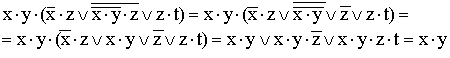 (используются правило де Моргана, закон двойного отрицания и закон
(используются правило де Моргана, закон двойного отрицания и закон
поглощения).
Из этих примеров видно, что при упрощении логических формул не всегда
очевидно, какой из законов алгебры логики следует применить на том или ином
шаге. Навыки приходят с опытом.
Обозначения[ | код]
Наиболее часто встречаются следующие обозначения для операции конъюнкции:
a∧b,a&&b,a&b,a⋅b,aANDb,min(a,b){\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}
(в случае использования точки, как знака логического умножения, этот знак, как и при обычном умножении в алгебре, может быть опущен: ab{\displaystyle ab}).
При этом обозначение a∧b{\displaystyle a\land b}, рекомендованное стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия). Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком ⋅{\displaystyle \cdot } — как обычное умножение. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930).
Обозначение для конъюнкции было использовано и в раннем языке программирования Алгол 60. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения и (с возможностью замены последнего на ключевое слово ); в языках Паскаль и Ада используется зарезервированное слово ; в языках C и C++ применяются обозначения для побитовой конъюнкции и для логической конъюнкции).
Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что <1{\displaystyle 0<1}), оказывается, что (a∧b)=min(a,b).{\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: (a∧b)=ab(modk){\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком {,…,k−1}{\displaystyle \{0,\dots ,k-1\}} полугруппы N{\displaystyle \mathbb {N} } натуральных чисел).
Примечания[ | код]
- ↑ , с. 264—266, 534—536.
- . // Website Online Etymology Dictionary. Дата обращения 7 февраля 2016.
- , с. 67.
- Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
- . // Website Jeff Miller Web Pages. Дата обращения 7 февраля 2016.
- , с. 30.
- Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
- Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
- Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
- , Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
- Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
- Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
- ↑ Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.
Логический оператор НЕ
Мы уже с ним сталкивались на уроке №34.
| Логический оператор НЕ (!) | |
| Операнд | Результат |
| true | false |
| false | true |
Если операндом является true, то, после применения логического НЕ, результатом будет false. Если же операнд до применения оператора НЕ был false, то после его применения — станет true. Другими словами, логический оператор НЕ меняет результат на противоположный начальному значению. Он часто используется в условных выражениях:
bool bTooLarge = (x > 100); // переменная bTooLarge будет true, если x > 100
if (!bTooLarge)
// Делаем что-нибудь с x
else
// Выводим ошибку
|
1 |
boolbTooLarge=(x>100);// переменная bTooLarge будет true, если x > 100 if(!bTooLarge) // Делаем что-нибудь с x else // Выводим ошибку |
Следует помнить, что логический оператор НЕ имеет очень высокий . Новички часто совершают следующую ошибку:
#include <iostream>
int main()
{
int x = 5;
int y = 7;
if (!x == y)
std::cout << «x does not equal y»;
else
std::cout << «x equals y»;
return 0;
}
|
1 |
#include <iostream> intmain() { intx=5; inty=7; if(!x==y) std::cout<<«x does not equal y»; else std::cout<<«x equals y»; return; } |
Результат выполнения программы:
Но ведь не равно , как это возможно? Поскольку приоритет логического оператора НЕ выше, чем приоритет оператора равенства, то выражение обрабатывается как . Так как — это , то — это . Условие ложное, поэтому выполняется часть else!
Напоминание: Любое ненулевое целое значение в логическом контексте является true. Так как , то вычисляется как true, а вот , т.е. . Использование целых чисел в логических операциях подобным образом может запутать не только пользователя, но и самого разработчика, поэтому так не рекомендуется делать!
Правильный способ написания программы, приведенной выше:
#include <iostream>
int main()
{
int x = 5;
int y = 7;
if (!(x == y))
std::cout << «x does not equal y»;
else
std::cout << «x equals y»;
return 0;
}
|
1 |
#include <iostream> intmain() { intx=5; inty=7; if(!(x==y)) std::cout<<«x does not equal y»; else std::cout<<«x equals y»; return; } |
Сначала обрабатывается , а затем уже оператор НЕ изменяет результат на противоположный.
Правило: Если логический оператор НЕ должен работать с результатами работы других операторов, то другие операторы и их операнды должны находиться в круглых скобках.
Многозначная логика
Операции, называемой в двоичной логике конъюнкция, в многозначных логиках обычно сопоставляется операция минимум: min(a,b){\displaystyle min(a,b)}, где a,b∈{,…,k−1},{\displaystyle a,b\in \{0,\dots ,k-1\},} а k{\displaystyle k} — значность логики; впрочем, возможны и другие варианты обобщения обычной конъюнкции на многозначный случай. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов {\displaystyle 0} и k−1{\displaystyle k-1}.
Название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.
Булева алгебра[ | код]
Определение.
Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).
Правило: результат равен наименьшему операнду.
Описание.
В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений ,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, true>false{\displaystyle true>false}, при цифровом обозначении старшинство естественно 1>{\displaystyle 1>0}.
Правило: результат равен 1{\displaystyle 1}, если все операнды равны 1{\displaystyle 1}; во всех остальных случаях результат равен {\displaystyle 0}.
Таблицы истинности:
для бинарной конъюнкции
| a{\displaystyle a} | b{\displaystyle b} | a∧b{\displaystyle a\land b} |
|---|---|---|
| {\displaystyle 0} | {\displaystyle 0} | {\displaystyle 0} |
| 1{\displaystyle 1} | {\displaystyle 0} | {\displaystyle 0} |
| {\displaystyle 0} | 1{\displaystyle 1} | {\displaystyle 0} |
| 1{\displaystyle 1} | 1{\displaystyle 1} | 1{\displaystyle 1} |
для тернарной конъюнкции
| a{\displaystyle a} | b{\displaystyle b} | c{\displaystyle c} | a∧b∧c{\displaystyle a\land b\land c} |
|---|---|---|---|
| 1 | |||
| 1 | |||
| 1 | 1 | ||
| 1 | |||
| 1 | 1 | ||
| 1 | 1 | ||
| 1 | 1 | 1 | 1 |
Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции.
Программирование
В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.
Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата false{\displaystyle false} или true{\displaystyle true}. Например:
if (a & b & c)
{
/* какие-то действия */
};
Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов.
Принцип работы условного «И» в аналогичной ситуации:
a = false; b = true; c = true;
if (a && b && c)
{
/* какие-то действия */
};
Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.
Результат будет равен true{\displaystyle true}, если оба операнда равны true{\displaystyle true} (для числовых типов не равны {\displaystyle 0}). В любом другом случае результат будет равен false{\displaystyle false}.
При этом применяется стандартное соглашение: если значение левого операнда равно false{\displaystyle false}, то значение правого операнда не вычисляется (вместо b{\displaystyle b} может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приёмом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую
{$B-}
или выключающую
{$B+}
подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:
if (a != && b a > 3)
{
/* какие-то действия */
};
В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдёт деления на ноль.
Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,
| если | |
| a = | 011001012{\displaystyle 01100101_{2}} |
| b = | 001010012{\displaystyle 00101001_{2}} |
| то | |
| a И b = | 001000012{\displaystyle 00100001_{2}} |
Классическая логика
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для дизъюнкции:
- a→a∨b{\displaystyle a\to a\lor b}
- b→a∨b{\displaystyle b\to a\lor b}
- (a→c)→((b→c)→((a∨b)→c)){\displaystyle (a\to c)\to ((b\to c)\to ((a\lor b)\to c))}
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции
Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.
3.5. Что такое схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений.
Условное обозначение на структурных схемах схемы И с двумя входами
представлено на рис. 3.1.
Рис. 3.1.
| x | y | x & y |
| 1 | ||
| 1 | ||
| 1 | 1 | 1 |
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах
будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет
ноль.
Связь между выходом z этой схемы и входами x и
y описывается соотношением: z = x & y
(читается как «x и y»). Операция конъюнкции на структурных схемах
обозначается знаком «&» (читается как
«амперсэнд»), являющимся сокращенной записью английского слова
and.
С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических
значений. Когда хотя бы на одном входе схемы ИЛИ будет
единица, на её выходе также будет единица.
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами
представлено на рис. 3.2. Знак «1» на схеме — от устаревшего
обозначения дизъюнкции как «>=1» (т.е. значение
дизъюнкции равно единице, если сумма значений операндов больше или равна 1).
Связь между выходом z этой схемы и входами
x и y описывается соотношением:
z = x v y (читается как «x или y»).
Рис. 3.2.
| x | y | x v y |
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 | 1 |
С х е м а НЕ
Схема НЕ (инвертор) реализует операцию отрицания.
Связь между входом x этой схемы и выходом
z можно записать соотношением z = ,
x где
читается как «не x» или «инверсия х».
Если на входе схемы 0, то на выходе 1.
Когда на входе 1, на выходе Условное
обозначение на структурных схемах инвертора — на рисунке 3.3.
Рис. 3.3.
| x | |
| 1 | |
| 1 |
С х е м а И—НЕ
Схема И—НЕ состоит из элемента И и инвертора и осуществляет
отрицание результата схемы И. Связь между выходом z и входами
x и y схемы записывают следующим образом: , где
читается как «инверсия x и y». Условное обозначение на
структурных схемах схемы И—НЕ с двумя входами представлено
на рисунке 3.4.
Рис. 3.4.
| x | y | |
| 1 | ||
| 1 | 1 | |
| 1 | 1 | |
| 1 | 1 |
С х е м а ИЛИ—НЕ
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и
осуществляет отрицание результата схемы ИЛИ. Связь между
выходом z и входами x и
y схемы записывают следующим образом: ,
где ,
читается как «инверсия x или y «. Условное
обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами
представлено на рис. 3.5.
Рис. 3.5.
| x | y | |
| 1 | ||
| 1 | ||
| 1 | ||
| 1 | 1 |