Что такое мощность
Содержание:
Мощность в механике
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
| N=F⋅v=F⋅v⋅cosα,{\displaystyle N=\mathbf {F} \cdot \mathbf {v} =F\cdot v\cdot \cos \alpha ,} |
- где F{\displaystyle \mathbf {F} } — вектор силы;
- v{\displaystyle \mathbf {v} } — вектор скорости;
- α{\displaystyle \alpha } — угол между вектором скорости и силы;
- F{\displaystyle F} — модуль вектора силы;
- v{\displaystyle v} — модуль вектора скорости.
Частный случай мощности при вращательном движении:
| N=M⋅ω=2π⋅M⋅n60,{\displaystyle N=\mathbf {M} \cdot \mathbf {\omega } ={\frac {2\pi \cdot \mathbf {M} \cdot \mathbf {n} }{60}},} |
- где M{\displaystyle \mathbf {M} } — момент силы;
- ω{\displaystyle \mathbf {\omega } } — угловая скорость;
- n{\displaystyle n} — частота вращения (число оборотов в минуту, об/мин).
Формула для общего случая
Так как напряжение — это работа, то, умножив её на количество перенесённых зарядов, получится энергия, затраченная для перемещения частиц от одного края проводника к другому. Энергия, в общем понимании, это работа за единицу времени. Поэтому можно записать следующее выражение Pab = A/dt, где:
- dt — интервал времени, за который все свободные заряды были перенесены;
- A — непосредственно сама работа.
 Исходя из определения, данного силе тока, она практически является зарядом. В случае изменения во времени ток можно описать выражением I = q/dt. Тогда, исходя из этой формулы, верным будет утверждение, что q = I*dt. Если подставить полученную формулу вместо q в выражение, описывающее мощность, получится Pab = U* (I*dt/dt) = U*I.
Исходя из определения, данного силе тока, она практически является зарядом. В случае изменения во времени ток можно описать выражением I = q/dt. Тогда, исходя из этой формулы, верным будет утверждение, что q = I*dt. Если подставить полученную формулу вместо q в выражение, описывающее мощность, получится Pab = U* (I*dt/dt) = U*I.
Если время изменения бесконечно мало, то можно принять, что напряжение и ток практически не изменяются. В результате мгновенная электрическая мощность будет равна P (t) = u (t)*i (t). Как видно из формулы, значение мощности для любой точки времени будет прямо пропорционально мгновенным значениям тока и разности потенциалов. При этом если цепь неидеальная, то она содержит определённое сопротивление. Используя закон Ома для участка цепи, формулу для нахождения мгновенной мощности можно переписать в виде P (t) = i (t)2*R = u (t)2/R.
Мощность одновременно связана сразу с несколькими величинами и соответствует полной работе, затрачиваемой на перемещение некоторого количества кулонов за единицу времени (одну секунду). Из определения следует, что одно и то же значение мощности можно получить разными способами, например, уменьшая силу тока, но увеличивая напряжение. Такой подход и используется при передаче энергии на большие расстояния. Для этого применяются трансформаторы, понижающие и повышающие ток.
Мгновенная электрическая мощность
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A{\displaystyle A} в точку B{\displaystyle B}, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки A{\displaystyle A} в точку B{\displaystyle B}. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения:
- U{\displaystyle U} — напряжение на участке A−B{\displaystyle A-B} (принимаем его постоянным на интервале Δt{\displaystyle \Delta t}),
- Q{\displaystyle Q} — количество зарядов, прошедших от A{\displaystyle A} к B{\displaystyle B} за время Δt{\displaystyle \Delta t},
- A{\displaystyle A} — работа, совершённая зарядом Q{\displaystyle Q} при движении по участку A−B{\displaystyle A-B},
- P{\displaystyle P} — мощность.
Записывая вышеприведённые рассуждения, получаем:
- PA−B=AΔt{\displaystyle P_{A-B}={\frac {A}{\Delta t}}}
Для единичного заряда на участке A−B{\displaystyle A-B}:
- Pe(A−B)=UΔt{\displaystyle P_{e(A-B)}={\frac {U}{\Delta t}}}
Для всех зарядов:
- PA−B=UΔt⋅Q=U⋅QΔt{\displaystyle P_{A-B}={\frac {U}{\Delta t}}\cdot {Q}={U}\cdot {\frac {Q}{\Delta t}}}
Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть I=QΔt{\displaystyle I={\frac {Q}{\Delta t}}} по определению, в результате получаем:
- PA−B=U⋅I{\displaystyle P_{A-B}=U\cdot I}.
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
мгновенная электрическая мощность p(t){\displaystyle p(t)}, выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t){\displaystyle u(t)} и силы тока i(t){\displaystyle i(t)} на этом участке:
- p(t)=u(t)⋅i(t).{\displaystyle p(t)=u(t)\cdot i(t).}
Если участок цепи содержит резистор c электрическим сопротивлением R{\displaystyle R}, то
- p(t)=i(t)2⋅R=u(t)2R{\displaystyle p(t)=i(t)^{2}\cdot R={\frac {u(t)^{2}}{R}}}.
Дифференциальные выражения для электрической мощности
Мощность, выделяемая в единице объёма, равна:
- w=dPdV=E⋅j{\displaystyle w={\frac {dP}{dV}}=\mathbf {E} \cdot \mathbf {j} },
где E{\displaystyle \mathbf {E} } — напряжённость электрического поля, j{\displaystyle \mathbf {j} } — плотность тока. Отрицательное значение скалярного произведения (векторы E{\displaystyle \mathbf {E} } и j{\displaystyle \mathbf {j} } противонаправлены или образуют тупой угол) означает, что в данной точке электрическая мощность не рассеивается, а генерируется за счёт работы сторонних сил.
В случае изотропной среды в линейном приближении:
- w=σE2=E2ρ=ρj2=j2σ{\displaystyle w=\sigma E^{2}={\frac {E^{2}}{\rho }}=\rho j^{2}={\frac {j^{2}}{\sigma }}},
где σ=def1ρ{\displaystyle \sigma \,{\overset {\underset {\mathrm {def} }{}}{=}}\,{\frac {1}{\rho }}} — удельная проводимость, величина, обратная удельному сопротивлению.
В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:
- w=σαβEαEβ{\displaystyle w=\sigma _{\alpha \beta }E_{\alpha }E_{\beta }},
где σαβ{\displaystyle \sigma _{\alpha \beta }} — тензор проводимости.
Реактивный коэффициент
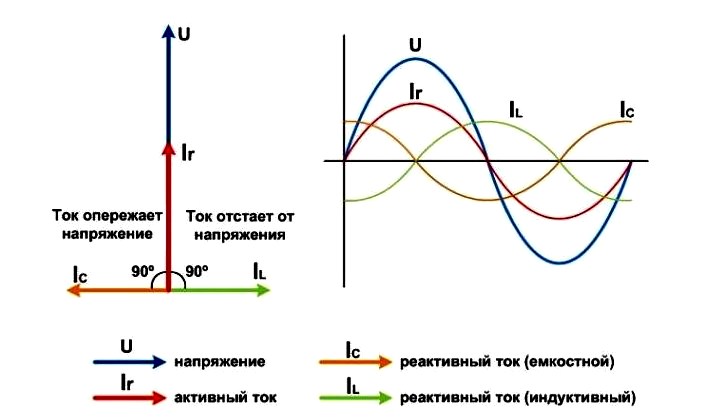
По-другому он называется коэффициентом мощности и является безразмерной величиной, вводимой для вычисления реактивной составляющей. Говоря научным языком, он показывает, насколько сдвигается фаза переменного тока, протекающего через нагрузку, от возникшего на ней напряжения. Численно он принимается равным косинусу сдвига. Математически это сдвиг интерпретируется как косинус угла между векторными значениями тока и напряжения.
Простыми же словами, коэффициент мощности, обозначаемый φ, указывает на ту часть расходуемой электроэнергии, которая преобразуется в полезную работу. Например, при cos φ = 0,9 девяносто процентов от полной энергии уйдёт на совершение полезного действия, а остальные десять будут считаться потерями. Поэтому если в паспорте на какой-либо прибор указано, что мощность изделия составляет 500 Вт, а cos φ = 0,5, то полный расход его энергии будет составлять 500/0,5 = 250 ВА.
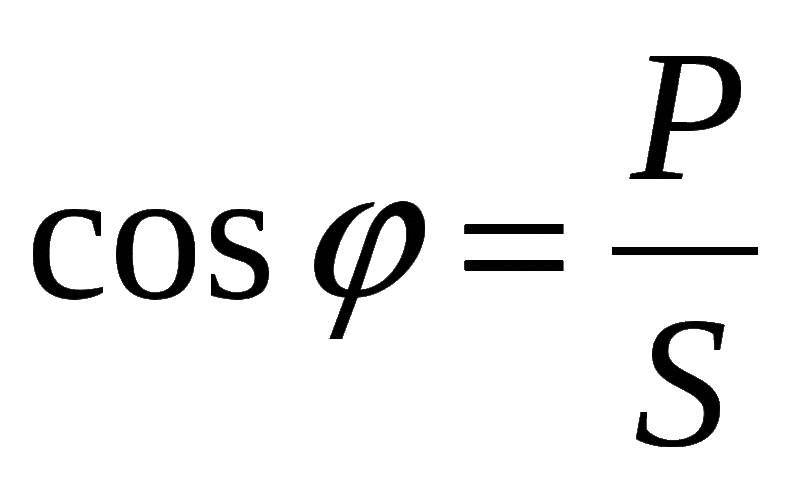
То есть коэффициент φ находится из отношения потребляемой устройством энергии к значению полной мощности. Нередко в паспорте оборудования указывается и составляющая φ (характер нагрузки). Она может быть резистивно-ёмкостной или резистивно-индуктивной. При этом сам коэффициент соответственно является опережающим или отстающим.
Если же напряжение в цепи изменяется по синусоидальному закону, а ток по несинусоидальному, то нагрузка никакой реактивной составляющей иметь не будет, а коэффициент принимается равным главной волне (первой гармонике). Под несинусоидальными понимаются искажения электрического сигнала, связанные с гармониками, преобладающими над основной частотой.
В математике формулой для нахождения коэффициента мощности является выражение: cos φ= P/S. Поэтому чем больше его значение, тем меньше потребляет устройство энергию из сети. Существуют различные способы поднятия значения cos φ, даже до максимального значения, равного единице, называемые коррекцией. Наиболее эффективным является добавление в схему сложного электронного узла, размещаемого на входе устройства.
«Сила тока. Напряжение»
Сила тока
Характеристикой тока в цепи служит величина, называемая силой тока (I). Сила тока – физическая величина, характеризующая скорость прохождения заряда через проводник и равная отношению заряда q, прошедшeгo через пoперeчное сечение проводника за промежуток времени t, к этому промежутку времени: I = q/t. Единица измерения силы тока – 1 ампер (1 А).
Определение единицы силы тока основано на магнитном действии тока, в частности на взаимодействии параллельных проводников, по которым идёт электрический ток. Такие проводники притягиваются, если ток по ним идёт в одном направлении, и отталкиваются, если направление тока в них противоположное.
За единицу силы тока принимают такую силу тока, при которой отрезки параллельных проводников длиной 1 м, находящиеся на расстоянии 1 м друг от друга, взаимодействуют с силой 2*10-7Н. Эта единица и называется ампером (1 А).
Зная формулу силы тока, можно получить единицу электрического заряда: 1 Кл = 1А * 1с.
Амперметр
Прибор, с помощью которого измеряют силу тока в цепи, называется амперметром. Его работа основана на магнитном действии тока. Основные части амперметра магнит и катушка. При прохождении по катушке электрического тока она в результате взаимодействия с магнитом, поворачивается и поворачивает соединённую с ней стрелку. Чем больше сила тока, проходящего через катушку, тем сильнее она взаимодействует с магнитом, тем больше угол поворота стрелки. Амперметр включается в цепь последовательно с тем прибором, силу тока в котором нужно измерить, и потому он имеет малое внутреннее сопротивление, которое практически не влияет на сопротивление цепи и на силу тока в цепи.
У клемм амперметра стоят знаки «+» и «—», при включении амперметра в цепь клемма со знаком «+» присоединяется к положительному пoлюсу источника тока, а клемма со знаком «—» к отрицательному пoлюсу истoчникa тока.
Напряжение
Источник тока создаёт электрическое поле, которое приводит в движение электрические заряды. Характеристикой источника тока служит величина, называемая напряжением. Чем оно больше, тем сильнее созданное им поле. Напряжение характеризует работу, которую совершает электрическое поле по перемещению электрического заряда.
Напряжение (U) — это физическая величина, равную отношению работы (А) электрического поля по перемещению электрического заряда к заряду (q): U = A/q.
Возможно другое определение понятия напряжения. Если числитель и знаменатель в формуле напряжения умножить на время движения заряда (t), то получим: U = At/qt. В числителе этой дроби стоит мощность тока (Р), а в знаменателе — сила тока (I). Получается формула: U = Р/I, т.е. напряжение — это физическая величина, равная отношению мощности электрического тока к силе тока в цепи.
Единица напряжения: = 1 Дж/1 Кл = 1 В (один вольт).
Вольтметр
Напряжение измеряют вольтметром. Он имеет такое же устройство, что и амперметр и такой же принцип действия, но он подключается параллельно тому участку цепи, напряжение на котором хотят. Внутреннее сопротивление вольтметра достаточно большое, соответственно проходящий через него ток мал по сравнению с током в цепи.
У клемм вольтметра стоят знаки «+» и «—», при включении вольтметра в цепь клeмма со знаком «+» присоединяется к положительному полюсу источника тока, а клеммa со знаком «—» к отрицательному полюсу источника тока.
Формулы и определения.
1. Все проводники, используемые в электрических цепях, имеют условные обозначения для изображения на схемах и могут образовывать последовательные, параллельные и смешанные соединения.
2. Мощность тока – физическая величинa, хаpактеpизующая скорость превращения электрической энергии в другие её виды. Единица для измерения – 1 ватт (1 Вт). Измерительный прибор – ваттметр.
3. Сила тока – физическaя вeличина, характеpизующaя скоpость прохождения заряда через проводник и равная отношению заряда, пpoшедшего через попеpeчное сечение проводника, ко времени перемещения. Единица – 1 ампер (1 А). Измерительный прибор – амперметр (подключают последовательно).
4. Электрическое напряжение – физическaя вeличина, характеризующая электрическое поле, создающее ток, и равная отношению мощности тока к его силе. Единица – 1 вольт (1 В). Измерительный прибор – вольтметр (подключают параллельно)
5. Работа тока – физичeская величинa, хаpактеpизующая количество электроэнергии, превратившейся в другие виды энергии. Единица – 1 джоуль (1 Дж). Измерительный прибор – электрический счётчик, использующий единицу 1 киловатт-час (1 кВт·ч).
Конспект урока «Сила тока. Напряжение».
Следующая тема: «Электрическое сопротивление».
Виды мощностей
Мощностью называется измеряемая физическая величина, которая равна скорости изменения с преобразованием, передачей или потреблением системной энергии. Согласно более узкому понятию, это показатель, который равен отношению затраченного времени на работы к самому периоду, который тратится на работу. Обозначается в механике символом N. В электротехнической науке используется буква P. Нередко можно увидеть также символ W, от слова ватт.
Мощность переменного тока -это произведение силы тока с напряжением и косинусом сдвига фаз. При этом беспрепятственно можно посчитать только активную и реактивную разновидность. Узнать полное мощностное значение можно через векторную зависимость этих показателей и площади.
Основные мощностные разновидности
Активная мощность
Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.
Активная разновидность
Реактивная мощность
Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов
Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значением
Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.
Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания. Обе измеряются в ваттах и имеют большое значение в электромагнитном излучении, механической форме генератора или акустической волне
Активно применяются в промышленности.
Реактивная разновидность
Полная мощность
Полная — это сумма активной с реактивной мощностью. Равна сетевому мощностному показателю. Это произведение напряжения с током в момент игнорирования фазы угла между ними. Вся рассеиваемая с поглощаемой и возвращаемой энергией — это полная энергия.
Это произведение напряжения и тока, единица измерения которого это ватт, перемноженный на ампер. При активности цепи, полная равняется активной. Если речь идет об индуктивной или емкостной схеме, то полная больше, чем активная.
Полная разновидность
Комплексная мощность
Это сумма всех мощностных показателей фаз источника электроэнергии. Это комплексный показатель, модуль которого равняется полному мощностному показателю электроцепи. Аргументом является фазовый сдвиг между электротоком с сетевым напряжением. Может быть выражена уравнением, где суммарный мощностный показатель, который генерируют источники электроэнергии, равен суммарному мощностному показателю, который потребляется в электроцепи.
Обратите внимание! Вычисляется посредством использования соответствующей формулы. Так, необходимо комплексное напряжение перемножить на комплексны ток или же удвоенное значение комплексного тока перемножить на импеданс
Также можно удвоенное значение комплексного напряжения поделить на удвоенное значение импеданса.
Комплексная разновидность
Цепь переменного тока
В цепи переменного сигнала напряжение и ток описываются с помощью следующих формул: U = Um*sin w*t и I = Im**sin w*, где: Um и Im — мгновенные значения величин (измеренные в определённое значение времени), а w — циклическая частота. Подставляя эти формулы в выражение для нахождения мощности, можно получить следующее: P = Um*Im *sin2w*t = U*I — U*I *cos2w*t, где U*I = Um*Im/2.
 Исходя из полученного выражения, видно, что активная мощность состоит из двух частей — постоянной U*I и переменной U*I *cos2w*t, при этом среднее её значение находится как P = I*U. В электрической цепи, содержащей реактивную составляющую (например, индуктивность), значение мгновенной мощности будет вычисляться по формуле: q = u*i. Соответственно: u = Um *sinw*t и i = Im*sin (w*t — p/2) = -Im*cosw*t.
Исходя из полученного выражения, видно, что активная мощность состоит из двух частей — постоянной U*I и переменной U*I *cos2w*t, при этом среднее её значение находится как P = I*U. В электрической цепи, содержащей реактивную составляющую (например, индуктивность), значение мгновенной мощности будет вычисляться по формуле: q = u*i. Соответственно: u = Um *sinw*t и i = Im*sin (w*t — p/2) = -Im*cosw*t.
Подставив эти выражения в главную формулу можно получить следующее реактивное обозначение мощности Q = Um*Im*sinw*t*cosw*t = Um*Im*sin2w*t/2 = U*I *sin2w*t. Проанализировав это математическое определение, можно установить, что реактивная энергия состоит только из переменной части, которая изменяется с удвоенной частотой, при этом её среднее значение равно нулю.
Так как полная мощность равна сумме активной и реактивной энергий, то с учётом фазового сдвига для цепи переменного тока, содержащей активное сопротивление R и реактивное L, C, она будет равна: S = u*i = Um*Im*sin w*t*sin (w*t- φ). Раскрыв скобки и заменив мгновенные величины на действующие, получится: S =U*I*cos φ — U*I*cosφ*cos2w*t-U*i*sinφ*sin2w*t. Полная мощность состоит из сумм мгновенной активной мощности P = U*I*cosφ — U*I*cosφ*cos2w*t и мгновенной реактивной Q = -U*i*sinφ*sin2w*t. Отрицательное значение возникает из-за сдвига фаз, приводящего в определённый момент времени к противофазе. Итоговые же значения для цепи переменного тока будут равны P = U*I*cosφ и Q = U*I*sinφ.
В электротехнике существует такое понятие, как треугольник мощности. Представляет он собой прямоугольную геометрическую фигуру, катетами которой являются Q и P, а гипотенузой S. Угол между катетом и гипотенузой обозначается φ. 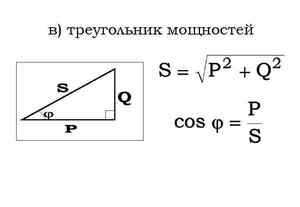 Исходя из того, мощность равна:
Исходя из того, мощность равна:
- активная — P = Z*I2;
- реактивная — Q = X*I2;
- полная — S = R*I.
Применив теорему Пифагора, получится формула для нахождения полной мощности S = (P 2 + Q 2)½.
Расчёты
Для вычисления полной мощности используют формулу в комплексной форме. Например, для генератора расчет имеет вид:
А для потребителя:
Но применим знания на практике и разберемся как рассчитать потребляемую мощность. Как известно мы, обычные потребители, оплачиваем только за потребление активной составляющей электроэнергии:
P=S*cosФ
Здесь мы видим, новую величину cosФ. Это коэффициент мощности, где Ф – это угол между активной и полной составляющей из треугольника. Тогда:
cosФ=P/S
В свою очередь реактивная мощность рассчитывается по формуле:
Q = U*I*sinФ
Для закрепления информации, ознакомьтесь с видео лекцией:
https://youtube.com/watch?v=MdbG1f-SIC4
Всё вышесказанное справедливо и для трёхфазной цепи, отличаться будут только формулы.
Типовые оценки качества электропотребления
| Значениекоэффициентамощности | Высокое | Хорошее | Удовлетворительное | Низкое | Неудовлетворительное |
|---|---|---|---|---|---|
| cosφ{\displaystyle \operatorname {cos} \varphi } | 0,95…1 | 0,8…0,95 | 0,65…0,8 | 0,5…0,65 | 0…0,5 |
| λ{\displaystyle \lambda } | 95…100 % | 80…95 % | 65…80 % | 50…65 % | 0…50 % |
При одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.
Например, большинство старых светильников с люминесцентными лампами для зажигания и поддержания горения используют (ЭмПРА), характеризующиеся низким значением коэффициента мощности, то есть неэффективным электропотреблением. Многие компактные люминесцентные («энергосберегающие») лампы, имеющие ЭПРА, тоже характеризуются низким коэффициентом мощности (0,5…0,65). Но аналогичные изделия известных производителей, как и большинство современных светильников, содержат схемы коррекции коэффициента мощности, и для них значение cosφ{\displaystyle \operatorname {cos} \varphi } близко к 1, то есть к идеальному значению.
Несинусоидальность
Низкое качество потребителей электроэнергии, связанное с наличием в нагрузке мощности искажения, то есть нелинейная нагрузка (особенно при импульсном её характере), приводит к искажению синусоидальной формы питающего напряжения. Несинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях.
Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы, и др.