Расчёт индуктивности. часть 2

Общие свойства катушек индуктивности

В зависимости от требуемой индуктивности и частоты, на которой катушка будет работать, она может иметь самые различные исполнения.

Для высоких частот это может быть простая катушка состоящая из нескольких витков провода или же катушка с сердечником из ферромагнитного материала и иметь индуктивность от нескольких наногенри до нескольких десятков миллигенри. Такие катушки применяются в радиоприемной, передающей, измерительной аппаратуре и т.п.

Катушки, работающие на высоких частотах, можно разделить на катушки контуров, катушки связи и дроссели высокой частоты. В свою очередь катушки контуров могут быть с постоянной индуктивностью и переменной индуктивностью (вариометры).

По конструктивному признаку высокочастотные катушки разделяются на однослойные и многослойные, экранированные и неэкранированные, катушки без сердечников и катушки с магнитными и немагнитными сердечниками, бескаркасные, цилиндрические плоские и печатные.

Для работы в цепи переменного тока низкой частоты, на звуковых частотах, во входных фильтрах блоков питания, в цепях питания осветительного электрооборудования применяются катушки с достаточно большой индуктивностью. Их индуктивность достигает десятки и даже сотни генри, а в обмотках могут создаваться большие напряжения и протекать значительные токи.

Для увеличения индуктивности при изготовлении таких катушек применяют магнитопроводы (сердечники), собранные из отдельных тонких изолированных пластин сделанных из специальных магнитных материалов – электротехнических сталей, пермаллоев и др.

Применение наборных магнитопроводов обусловлено тем, что под действием переменного магнитного поля в сплошном магнитопроводе, который можно рассматривать как множество короткозамкнутых витков, образуются вихревые токи, которые нагревают магнитопровод, бесполезно потребляя часть энергии магнитного поля. Изоляция же между слоями стали оказывается на пути вихревых токов и значительно снижает потери.

Катушки с магнитопроводами из изолированных пластин можно разделить на дроссели и трансформаторы.

Что это такое?

Катушка представляет собой трансформатор. Целью устройства является повышение параметров тока до огромных высот (вплоть до миллионов вольт). Основная цель: повысить до максимума частоту переменного тока. В идеале, в точке приема энергии должна находится такая же обратная катушка, которая вступит в резонанс с устройством, что позволит передать энергию на расстояние.

Передача энергии без проводника катушкой Тесла

Разберем подробности того, как работает катушка Тесла. Для начала колебания: не сразу ясно, что колеблется в катушке. Постоянный ток, который использовал в своих изобретениях Эдисон дорог в производстве. Такая энергия имеет один, ярко выраженный вектор движения. Переменный ток постоянно меняет параметры электричества: напряжения и силы тока. Это и называется колебаниями электрического тока.

Интересно, что совпадают основные законы колебания электрического тока и механического маятника. В частности, для электричества так же существует эффект резонанса. При совпадении частот двух электрополей амплитуда колебаний становится больше. По задумке Тесло после вступления катушек в резонанс в приемнике должен был появиться электрический ток.

В реальности приемник так и не был изобретен. Катушка Теса используется в качестве пособия, на ней можно увидеть стрим: проще говоря электрическую дугу, проскользнувший разряд, искусственную молнию и для изучения беспроводной передачи электричества.

Расчет катушек индуктивности под конкретный провод

Пересчет катушек индуктивности производится при отсутствии провода нужного диаметра, указанного в описании конструкции, и замене его проводом другого диаметра, а также при изменении диаметра каркаса катушки.Если отсутствует провод нужного диаметра, можно воспользоваться другим. Изменение диаметра в пределах до 25% в ту или другую сторону вполне допустимо и, как правило, не отражается на качестве работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как при этом уменьшается омическое сопротивление катушки и повышается ее добротность. Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше допустимой величины.Пересчет количества витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле

где n — новое количество витков катушки; n1 — число витков катушки, указанное в описании; d — диаметр имеющегося провода; d1 — диаметр провода, указанного в описании. В качестве примера приведем пересчет числа витков катушки, изображенной на рис.1, для провода диаметром 0,8 мм

(длина намотки l = 18×0,8 — 14,4 мм).Таким образом, количество витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:

При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков. Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра на равное число процентов увеличивается количество витков. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса. В качестве примера произведем пересчет числа витков катушки, имеющей 40 витков при длине намотки 2 см и диаметр каркаса 1,5 см, на диаметр, равный 1,8 см. Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%. Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке на каркас большого диаметра нужно уменьшить число витков на 20%, или на 8 витков. Новая катушка будет иметь 32 витка. Длина намотки также уменьшится на 20%, или до 1,6 см.Проверим пересчет и определим допущенную погрешность. Исходная катушка имеет индуктивность:

Индуктивность новой катушки на каркасе с увеличенным диаметром:

Ошибка при пересчете составляет 0,32 мкГн, то есть меньше 2,5%, что вполне допустимо для расчетов в радиолюбительской практике.

Каждый любитель мастерить электронные приборы и , не раз сталкивался с необходимостью намотать катушку индуктивности или дроссель. В схемах конечно указывают число намотки катушки и каким проводом, но что делать если указанного диаметра провода нет в наличии, а есть намного толще или тоньше??

Я расскажу вам как это сделать на моем примере.Хотел я сделать вот эту схему . Намоточные данные катушек в схеме указаны (6 витков провода 0.4 на каркасе 2мм) эти намоточные данные соответствуют 47nH-нано Генри, все бы нормально но провод у меня был 0.6мм. Помощь я нашел в программе Coil32.

Открываем программу

Для этого вставляем в окошки известные нам данные этих катушек, длину намотки подбираем до тех пор пока вычисления не совпадут с нашими данными.

Но если вы например уже вытравили платы, а размер контактов для катушки остался прежним, то есть для катушки с длиной намотки 3мм, а у вас же получилась на 5.5мм (намного больше и впаять рядом 3 таких катушки будет проблематично)

Значит нужно нашу катушку уменьшить, ставим в окошко диаметр каркаса не 2мм, а 4мм. И наша катушка с проводом 0.6мм, уменьшается в длине с 5.5мм до 3мм и число витков 3.5, +/- 1-2 нГн роли большой не сыграет, зато мы сможем легко впаять наши индуктивности.

Для того, чтобы создать магнитное поле и сгладить в нем помехи и импульсы, используются специальные накопительные элементы. Катушки индуктивности в цепи переменного тока и постоянного применяются для накопления определенного количества энергии и ограничения электричества.

Теоретическое обоснование

Если в проводящем контуре течёт ток, то ток создаёт магнитное поле.

Будем вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля достаточно слабы либо меняются достаточно медленно, чтобы можно было пренебречь порождаемыми ими магнитными полями.

Ток считаем одинаковым по всей длине контура (пренебрегая ёмкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).

По закону Био — Савара — Лапласа, величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства, пропорциональна этому току. Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником, также пропорционально порождающему току.

Рассуждение выше верно для вакуума. В случае присутствия магнитной среды (магнетика) с заметной (или даже большой) магнитной восприимчивостью, вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме). Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остаётся пропорциональным порождающему его току.

Тогда магнитный поток, то есть поток поля вектора магнитной индукции:

Φ=∫SB⋅dS{\displaystyle \Phi =\int \limits _{S}\mathbf {B} \cdot \mathbf {dS} }

через любую конкретную фиксированную поверхность S (в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току B всюду под интегралом.

Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной. На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближённо рассчитать поток через неё (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже). Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой).

Итак, мы обосновали:

Φ {\displaystyle \Phi \ }~ I,{\displaystyle \ I,}

этого достаточно, чтобы утверждать, введя обозначение L для коэффициента пропорциональности, что

Φ=LI.{\displaystyle \Phi =LI.}

В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур. (Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть её краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй). Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.

Но это действительно так: возьмём две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.

Принцип работы классической катушки Тесла

Классическое устройство катушки Тесла состоит из следующих элементов:

• Первичная обмотка, которая состоит из большого количества витков, порядка 800-1200 шт, провода малого диаметра.
• Вторичная обмотка. Это провод сравнительно большого диаметра. Катушка включает в себя меньшее количество витков.
• Конденсатор. Это накопитель заряда, который требуется для запуска первичной работы катушки.
• Разрядник. Два металлических шарика, которые находятся на небольшом расстоянии друг от друга.
• Сфера для распространения магнитного поля.

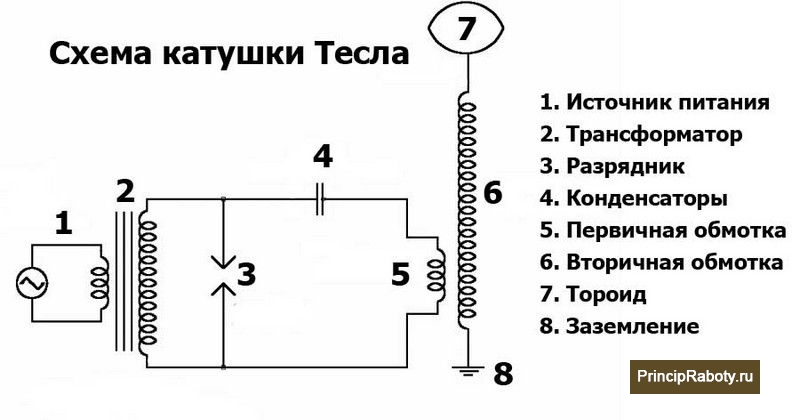Схема катушки Тесла

Первичная обмотка находится внутри вторичной. Разделителем служит обычная ПВХ труба. Разберем поэтапную работу катушки:

1. При подключении к сети в конденсаторе накапливается заряд.
2. Накопление заряда вызывает рост разности потенциалов между шариками разрядника. В итоге, как только напряжение достигает определенного значения, происходит стрим, то есть появляется электрическая дуга, которая соединяет между собой две части сети. Стрим в конструкции играет роль ключа-соединителя, который открывается при условии подходящих параметров напряжения.
3. Ток начинает течь первичной обмотке, создавая переменное магнитное поля. В свою очередь это переменное магнитное поле создает электричество во вторичной обмотке: явление индукции в действии.
4. В свою очередь ток вторичной обмотки создает магнитное поле, создающее индукционный ток в сфере. Ток в сфере вновь вызывает переменное магнитное поле, которое расходится в пространстве.
5. Если поднести к такой катушке электролампу, то она будет светится без всяческих проводов и источников электроэнергии. Собственно, источником в данном случае служит катушка.

Вот такая схема работы катушки Тесла.

Примечания

Если контур многовитковый (катушка) или вообще сложной формы, поверхность, краем которой он будет являться, может иметь достаточно сложную форму. Это никак не сказывается на большей части общих утверждений, однако для упрощения конкретного понимания ситуации и количественных оценок в случае катушки обычно приближенно рассматривают эту поверхность как совокупность («стопку») отдельных листков, каждый из которых привязан к отдельному единичному витку, а общий поток через такую поверхность рассматривается приближенно как сумма потоков через все такие листки.

Касаткин А. С. Основы электротехники. М.:Высшая школа, 1986.

Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. М.:Высшая школа, 1978.

↑ Индуктивность — статья из Большой советской энциклопедии. 

Правда, этот случай в принципе выходит за рамки квазистационарного приближения, позволяющего рассматривать элементы схемы как независимые, то есть понятие индуктивности отдельного элемента цепи начинает терять четкий смысл; однако оно во всяком случае может быть использовано хотя бы для оценочного расчета.

Прежде всего использование таких устройств, не основанных на электромагнитной индукции, обусловлено такими причинами, как необходимость или желательность иметь меньший размер элемента, чем это возможно для катушки индуктивности; например — в микросхемах, а также для элементов очень большой индуктивности.

Генри (единица индуктивности) — статья из Большой советской энциклопедии. 

Индуктивность // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2.

Glenn Elert. (1998–2008).

Michael W. Davidson. (1995–2008)

Генри Джозеф — статья из Большой советской энциклопедии. 

Присутствие магнетика особенно важно для катушек с ферромагнитным сердечником и т. п.

Здесь имеется в виду настоящая индуктивность; в электронике можно создать искусственно элементы (не основанные на явлении самоиндукции), зависимость ЭДС в которых от производной тока будет такой же, как в катушке индуктивности, но с коэффициентом противоположного знака — такие элементы можно условно назвать (по их поведению в электрической цепи) элементами с отрицательной индуктивностью, однако они не имеют отношения к предмету данной статьи.

Если считать структуру токов (точно или приближенно) фиксированной, то есть если токи не перераспределяются по объёму проводника в процессе их возбуждения.

Потокосцепление — статья из Большой советской энциклопедии. 

* Сивухин Д. В. Общий курс физики. — М.. — Т. III

Электричество.

Как и в других случаях, присутствие магнетика, особенно если это ферромагнетик, для какового всегда имеет место гистерезис, приводит к более или менее существенной нелинейности (особенно большой для магнитожестких материалов сердечника); поэтому формулу для индуктивности, подразумевающей именно линейное приближение, следует считать приближенной, а в общем случае в качестве магнитной проницаемости в формулу входит некоторая эффективная величина, зависящая от величины тока в катушке.

↑ Физическая энциклопедия, Главный редактор А. М. Прохоров. Индуктивность // Физический энциклопедический словарь. — Советская энциклопедия (рус.). — М., 1983.

Lorenz, L. Über die Fortpflanzung der Elektrizität // Annalen der Physik. — 1879. — Т. VII. — С. 161—193. (The expression given is the inductance of a cylinder with a current around its surface)..

Elliott, R. S. Electromagnetics. — New York: Institute of Electrical and Electronics Engineers, 1993. Замечание: Постоянная −3/2 неправильна.

Rosa, E.B. The Self and Mutual Inductances of Linear Conductors (англ.) // Bulletin of the Bureau of Standards : journal. — 1908. — Vol. 4, no. 2. — P. 301—344.

Что влияет на индуктивность?

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов.  Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

LC-метр  показывает 21 микрогенри.

Ввожу катушку на середину феррита

35 микрогенри. Уже лучше.

Продолжаю вводить катушку на правый край феррита

20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине.  Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности  в переменных катушках индуктивности:

где

1 – это каркас катушки

2 – это витки катушки

3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.

Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки

Индуктивность стала почти 50 микрогенри!

А давайте-ка попробуем расправим витки по всему ферриту

13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.

Убавим витки катушки в два раза. Было 24 витка, стало 12.

Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз.  Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.

Давайте поэкспериментируем с ферритовым кольцом.

Замеряем индуктивность

15 микрогенри

Отдалим витки катушки друг от друга

Замеряем снова

Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка  не играет никакой роли в катушке индуктивности тороидального исполнения.

Мотнем побольше витков. Было 3 витка, стало 9.

Замеряем

Офигеть! Увеличил количество витков  в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.

Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.

Для чего нужна катушка индуктивности

Стандартная конструкция катушки индуктивности состоит из изолированного провода с одной или несколькими жилами, намотанными в виде спирали на каркас из диэлектрика, имеющего прямоугольную, цилиндрическую или тороидальную форму. Иногда, конструкции катушек бывают бескаркасными. Наматывание провода производится в один или несколько слоев.

Для того, чтобы увеличить индуктивность, используются сердечники из ферромагнитов. Они же позволяют изменять индуктивность в определенных пределах. Не всем до конца понятно, для чего нужна катушка индуктивности. Ее используют в электрических цепях, как хороший проводник постоянного тока. Однако, при возникновении самоиндукции, возникает сопротивление, препятствующее прохождению переменного тока.

Разновидности катушек индуктивности

Существует несколько вариантов конструкций катушек индуктивности, свойства которых определяют и сферу их использования. Например, применение контурных катушек индуктивности вместе с конденсаторами, позволяют получать резонансные контуры. Они отличаются высокой стабильностью, качеством и точностью.

Катушки связи обеспечивают индуктивную связь отдельных цепей и каскадов. Таким образом, становится возможным деление базы и цепей по постоянному току. Здесь не требуется высокой точностью, поэтому, для этих катушек используется тонкий провод, наматываемый в две небольшие обмотки. Параметры данных приборов определяются в соответствии с индуктивностью и коэффициентом связи.

Некоторые катушки используются в качестве вариометров. Во время эксплуатации их индуктивность может изменяться, что позволяет успешно перестраивать колебательные контуры. Весь прибор включает в себя две последовательно соединенных катушки. Подвижная катушка вращается внутри неподвижной катушки, тем самым, создавая изменение индуктивности. Фактически, они являются статором и ротором. Если их положение изменится, то поменяется и значение самоиндукции. В результате, индуктивность прибора может измениться в 4-5 раз.

В виде дросселей используются те приборы, у которых при переменном токе отмечается высокое сопротивление, а при постоянном – очень низкое. Благодаря этому свойству, они используются в радиотехнических устройствах в качестве фильтрующих элементов. При частоте 50-60 герц для изготовления их сердечников применяется трансформаторная сталь. Если частота имеет более высокое значение, то сердечники изготавливаются из феррита или пермаллоя. Отдельные разновидности дросселей можно наблюдать в виде так называемых бочонков, подавляющих помехи на проводах.

Где применяются катушки индуктивности

Сфера применения каждого такого прибора, тесно связана с особенностями его конструкции. Поэтому нужно обязательно учитывать ее индивидуальные свойства и технические характеристики.

Совместно с резисторами или конденсаторами, катушки задействованы в различных цепях, имеющих частотно-зависимые свойства. Прежде всего, это фильтры, колебательные контуры, цепи обратной связи и прочее. Все виды этих приборов способствуют накоплению энергии, преобразованию уровней напряжения в импульсном стабилизаторе.

При индуктивной связи между собой двух и более катушек, происходит образование трансформатора. Эти приборы могут использоваться, как электромагниты, а также, как источник энергии, возбуждающий индуктивно связанную плазму.

Индуктивные катушки успешно используются в радиотехнике, в качестве излучателя и приемника в конструкциях кольцевых и магнитных антенн, работающих с электромагнитными волнами.